Giải các bất phương trình sau:
a) \(2{x^2} - 3x + 1 > 0\)
b) \({x^2} + 5x + 4 < 0\)
c) \( - 3{x^2} + 12x - 12 \ge 0\)
d) \(2{x^2} + 2x + 1 < 0.\)
- Tìm nghiệm của các phương trình trên
- Lập bảng xét dấu
- Kết luận tập nghiệm của bất phương trình
a) \(2{x^2} - 3x + 1 > 0\)
Tam thức \(f\left( x \right) = 2{x^2} - 3x + 1\) có \(a + b + c = 2 - 3 + 1 = 0\) nên hai nghiệm phân biệt \({x_1} = 1\) và \({x_2} = \frac{1}{2}.\)
Mặt khác \(a = 2 > 0,\) do đó ta có bảng xét dấu sau:
Tập nghiệm của bất phương trình là: \(S= \left( { - \infty ;\frac{1}{2}} \right) \cup \left( {1; + \infty } \right).\)
b) \({x^2} + 5x + 4 < 0\)
Tam thức \(f\left( x \right) = {x^2} + 5x + 4\) có \(a - b + c = 1 - 5 + 4 = 0\) nên phương trình có hai nghiệm phân biệt \(x = - 1\) và \(x = - 4.\)
Mặt khác \(a = 1 > 0,\) do đó ta có bảng xét dấu sau:
Tập nghiệm của bất phương trình là: \(S = \left( { - 4; - 1} \right).\)
c) \( - 3{x^2} + 12x - 12 \ge 0\)
Tam thức \(f\left( x \right) = - 3{x^2} + 12x - 12 = - 3\left( {{x^2} - 4x + 4} \right) = - 3{\left( {x - 2} \right)^2} \le 0\)
Do đó
\( - 3{x^2} + 12x - 12 \ge 0 \Leftrightarrow - 3{x^2} + 12x - 12 = 0 \Leftrightarrow - 3{\left( {x - 2} \right)^2} = 0 \Leftrightarrow x = 2.\)
Tập nghiệm của bất phương trình là: \(S = \left( { 2} \right).\)
d) \(2{x^2} + 2x + 1 < 0.\)
Tam thức \(f\left( x \right) = 2{x^2} + 2x + 1\) có \(\Delta = - 1 < 0,\) hệ số \(a = 2 > 0\) nên \(f\left( x \right)\) luôn dướng với mọi \(x,\) tức là \(2{x^2} + 2x + 1 > 0\) với mọi \(x \in \mathbb{R}.\)
\( \Rightarrow \) bất phương trình vô nghiệm

Các bài tập cùng chuyên đề
Bài 1 :
Giải bất phương trình \( - 2{x^2} + 3x - 7 \ge 0.\)
-
A.
\(S = 0.\)
-
B.
\(S = \left\{ 0 \right\}.\)
-
C.
\(S = \emptyset .\)
-
D.
\(S = \mathbb{R}.\)
Bài 2 :
Cho bất phương trình \({x^2} - 8x + 7 \ge 0\). Trong các tập hợp sau đây, tập nào có chứa phần tử không phải là nghiệm của bất phương trình?
-
A.
\(\left( { - \infty ;0} \right].\)
-
B.
\(\left[ {8; + \infty } \right).\)
-
C.
\(\left( { - \infty ;1} \right].\)
-
D.
\(\left[ {6; + \infty } \right).\)
Bài 3 :
Bất phương trình nào sau đây có tập nghiệm là \(\mathbb{R}\)?
-
A.
\( - 3{x^2} + x - 1 \ge 0.\)
-
B.
\( - 3{x^2} + x - 1 > 0.\)
-
C.
\( - 3{x^2} + x - 1 < 0.\)
-
D.
\(3{x^2} + x - 1 \le 0.\)
Bài 4 :
Tập hợp nào dưới đây chứa phần tử không là nghiệm của bất phương trình $\sqrt 2 {x^2} - \left( {\sqrt 2 + 1} \right)x + 1 < 0$?
-
A.
$\left( {\dfrac{{\sqrt 2 }}{2};1} \right)$
-
B.
$\left( {\dfrac{{\sqrt 2 }}{2};\dfrac{1}{2}} \right)$
-
C.
$\left[ {\dfrac{{\sqrt 2 }}{2};1} \right]$
-
D.
$\left( {\dfrac{{\sqrt 3 }}{2};1} \right)$
Bài 5 :
Bất phương trình \({x^2} - 6\sqrt 2 x + 18 \ge 0\) có tập nghiệm là:
-
A.
\(S = \mathbb{R}\)
-
B.
\(S = \emptyset \)
-
C.
\(S = \left( {3\sqrt 2 ;\,\, + \infty } \right)\)
-
D.
\(S = \mathbb{R}\backslash \left\{ {3\sqrt 2 } \right\}\)
Bài 6 :
Tập nghiệm của bất phương trình \(2x\left( {2 - x} \right) \ge 2 - x\) là
-
A.
\(\left[ {\dfrac{1}{2};2} \right]\)
-
B.
\(\left[ {\dfrac{1}{2}; + \infty } \right)\)
-
C.
\(\left[ {0; + \infty } \right)\)
-
D.
\(\left( { - \infty ;\dfrac{1}{2}} \right] \cup \left[ {2; + \infty } \right)\)
Bài 7 :
Tập nghiệm của bất phương trình \({x^2} + 5x - 6 \le 0\) là:
-
A.
\(\left[ { - {\rm{ 6}};{\rm{1}}} \right]\).
-
B.
\(\left[ {{\rm{2}};{\rm{3}}} \right]\).
-
C.
\(\left( { - \infty ;{\rm{6}}} \right] \cup \left[ {{\rm{1}}; + \infty } \right)\).
-
D.
\(\left( { - \infty ;{\rm{2}}} \right] \cup \left[ {{\rm{3}}; + \infty } \right)\).
Bài 8 :
Tập nghiệm của bất phương trình \( - {x^2} + 5x + 6 > 0\) là:-
A.
\(\left( { - 1;6} \right)\)
-
B.
\(\left\{ { - 1;6} \right\}\)
-
C.
\(\left[ { - 1;6} \right]\)
-
D.
\(\left( { - \infty ; - 1} \right) \cup \left( {6; + \infty } \right)\)
Bài 9 :
Giải mỗi bất phương trình bậc hai sau bằng cách sử dụng đồ thị:
a) \({x^2} + 2x + 2 > 0\)
b) \( - 3{x^2} + 2x - 1 > 0\)
Bài 10 :
Cho bất phương trình \({x^2} - 4x + 3 > 0\left( 2 \right)\).
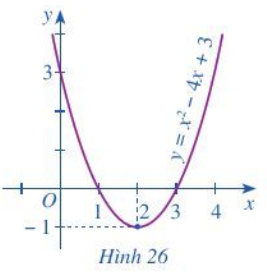
Quan sát parabol \(\left( P \right):{x^2} - 4x + 3\) ở Hình 26 và cho biết:
a) Bất phương trình (2) biểu diễn phần parabol (P) nằm ở phía nào của trục hoành.
b) Phần parabol (P) nằm phía trên trục hoành ứng với những giá trị nào của x.
Bài 11 :
Giải các bất phương trình bậc hai sau:
a) \(3{x^2} - 2x + 4 \le 0\)
b) \( - {x^2} + 6x - 9 \ge 0\)
Bài 12 :
a) Lập bảng xét dấu của tam thức bậc hai \(f\left( x \right) = {x^2} - x - 2\)
b) Giải bất phương trình \({x^2} - x - 2 > 0\)
Bài 13 :
Giải các bất phương trình bậc hai sau:
a) \(2{x^2} - 5x + 3 > 0\)
b) \( - {x^2} - 2x + 8 \le 0\)
c) \(4{x^2} - 12x + 9 < 0\)
d) \( - 3{x^2} + 7x - 4 \ge 0\)
Bài 14 :
Tìm m để phương trình \(2{x^2} + \left( {m + 1} \right)x + m - 8 = 0\) có nghiệm.
Bài 15 :
Giải các bất phương trình sau:
a) \(2{x^2} + 3x + 1 \ge 0\)
b) \( - 3{x^2} + x + 1 > 0\)
c) \(4{x^2} + 4x + 1 \ge 0\)
d) \( - 16{x^2} + 8x - 1 < 0\)
e) \(2{x^2} + x + 3 < 0\)
g) \( - 3{x^2} + 4x - 5 < 0\)
Bài 16 :
Tập nghiệm của bất phương trình \({x^2} - 3x + 2 < 0\) là:
-
A.
(1; 2)
-
B.
\(\left( {-\infty ;{\rm{ }}1} \right){\rm{ }} \cup {\rm{ }}\left( {2;{\rm{ }} + \infty } \right)\)
-
C.
\(\left( {-\infty ;{\rm{ }}1} \right)\)
-
D.
\(\left( {2;{\rm{ }} + \infty } \right)\)
Bài 17 :
Tập nghiệm của bất phương trình \({x^2}-{\rm{ }}1{\rm{ }} > {\rm{ }}0\) là:
-
A.
\(\left( {1; + \infty } \right)\)
-
B.
\(\left( { - 1; + \infty } \right)\)
-
C.
(– 1; 1);
-
D.
\(\left( { - \infty ; - 1} \right) \cup \left( {1; + \infty } \right)\)
Bài 18 :
Tập nghiệm của bất phương trình \( - {x^2} + 3x + 18 \ge 0\) là:
A. \(\left[ { - 3;6} \right]\)
B. \(\left( { - 3;6} \right)\)
C. \(x \in \left( { - \infty ; - 3} \right) \cup \left( {6; + \infty } \right)\)
D. \(x \in \left( { - \infty ; - 3} \right] \cup \left[ {6; + \infty } \right)\)
Bài 19 :
Giải các bất phương trình bậc hai sau:
a) \(3{x^2} - 8x + 5 > 0\)
b) \( - 2{x^2} - x + 3 \le 0\)
c) \(25{x^2} - 10x + 1 < 0\)
d) \( - 4{x^2} + 5x + 9 \ge 0\)
Bài 20 :
Tìm giao các tập nghiệm của hai bất phương trình \( - 3{x^2} + 7x + 10 \ge 0\) và \( - 2{x^2} - 9x + 11 > 0\).
Bài 21 :
Tìm \(m\) để phương trình \( - {x^2} + \left( {m + 2} \right)x + 2m - 10 = 0\) có nghiệm.
Bài 22 :
Tập nghiệm của bất phương trình \( - 5{x^2} + 6x + 11 \le 0\) là:
A. \(\left[ { - 1;\frac{{11}}{5}} \right]\)
B. \(\left( { - 1;\frac{{11}}{5}} \right)\)
C. \(x \in \left( { - \infty ; - 1} \right) \cup \left( {\frac{{11}}{5}; + \infty } \right)\)
D. \(x \in \left( { - \infty ; - 1} \right] \cup \left[ {\frac{{11}}{5}; + \infty } \right)\)
Bài 23 :
Giải các bất phương trình bậc hai sau:
a) \(4{x^2} - 9x + 5 \le 0\)
b) \( - 3{x^2} - x + 4 > 0\)
c) \(36{x^2} - 12x + 1 > 0\)
d) \( - 7{x^2} + 5x + 2 < 0\)
Bài 24 :
Giải các bất phương trình sau:
a) \( - 5{x^2} + x - 1 \le 0\)
b) \({x^2} - 8x + 16 \le 0\)
c) \({x^2} - x + 6 > 0\)
Bài 25 :
Giải các bất phương trình bậc hai:
a) \({x^2} - 1 \ge 0\)
b) \({x^2} - 2x - 1 < 0\)
c) \( - 3{x^2} + 12x + 1 \le 0\)
d) \(5{x^2} + x + 1 \ge 0\)
Bài 26 :
Bất phương trình \({x^2} - 2mx + 4 > 0\) nghiệm đúng với mọi \(x \in \mathbb{R}\) khi
A. \(m = - 1.\)
B. \(m = - 2.\)
C. \(m = 2.\)
D. \(m > 2.\)
Bài 27 :
Hãy giải bất phương trình lập được trong hoạt động khám phá và tìm giá bán gạo sao cho cửa hàng có lãi.
Bài 28 :
Giải các bất phương trình bậc hai sau:
a) \(15{x^2} + 7x - 2 \le 0\)
b) \( - 2{x^2} + x - 3 < 0\)
Bài 29 :
Dựa vào đồ thị của hàm số bậc hai tương ứng, hãy xác định tập nghiệm của các bất phương trình bậc hai sau đây:
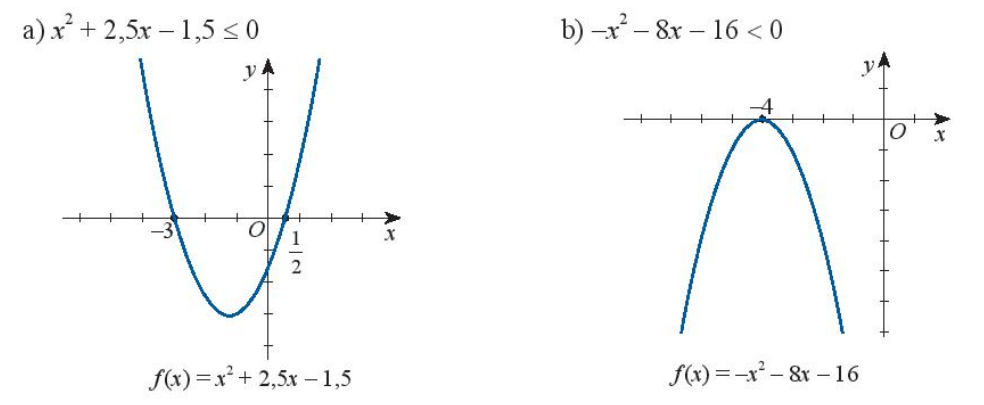
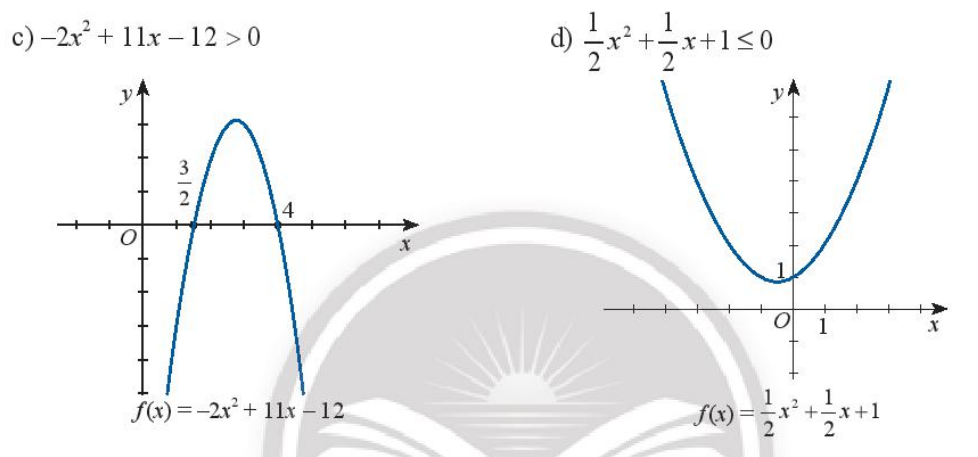
Bài 30 :
Giải các bất phương trình bậc hai sau:
a) \(2{x^2} - 15x + 28 \ge 0\)
b) \( - 2{x^2} + 19x + 255 > 0\)
c) \(12{x^2} < 12x - 8\)
d) \({x^2} + x - 1 \ge 5{x^2} - 3x\)




















Danh sách bình luận