Đề bài

Cho hình chóp đều $S.ABCD$ có các cạnh bên và các cạnh đáy đều bằng $a$.

a) Chứng minh rằng các tam giác $ASC$ và $BSD$ là tam giác vuông cân.

b) Gọi $O$ là giao điểm của $AC$ và $B{\rm{D}}$, chứng minh rằng đường thẳng $SO$ vuông góc với mặt phẳng $\left( {ABCD} \right)$.

c) Chứng minh rằng góc giữa đường thẳng $SA$ và mặt phẳng $\left( {ABCD} \right)$ bằng ${45^ \circ }$.

Phương pháp giải

a) Chứng minh tam giác có 2 cạnh bằng nhau và có một góc vuông.

b) Cách chứng minh đường thẳng vuông góc với mặt phẳng: chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.

c) Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.

Lời giải của GV Loigiaihay.com

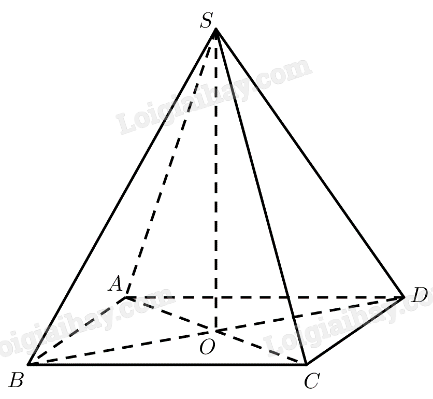
a) $ABCD$ là hình vuông $\Rightarrow AC = B{\rm{D}} = \sqrt {A{B^2} + B{C^2}}  = a\sqrt 2$

Xét $\Delta ASC$ có: $S{A^2} + S{C^2} = 2{a^2} = A{C^2},SA = SC$

Vậy tam giác $ASC$ là tam giác vuông cân tại $S$.

Xét $\Delta BSD$ có: $S{B^2} + S{D^2} = 2{a^2} = B{{\rm{D}}^2},SB = SD$

Vậy tam giác $BSD$ là tam giác vuông cân tại $S$.

b) $\Delta ASC$ vuông cân tại $S$ $\Rightarrow SO \bot AC$

$\Delta BSD$ vuông cân tại $S$ $\Rightarrow SO \bot B{\rm{D}}$

$\Rightarrow SO \bot \left( {ABCD} \right)$

c) $SO \bot \left( {ABCD} \right) \Rightarrow \left( {SA,\left( {ABCD} \right)} \right) = \left( {SA,OA} \right) = \widehat {SAO}$

$\Delta ASC$ vuông cân tại $S$ $\Rightarrow \widehat {SAO} = {45^ \circ }$

Vậy $\left( {SA,\left( {ABCD} \right)} \right) = {45^ \circ }$.