Đề bài

Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3). Tọa độ vecto \(\overrightarrow {OA} \) là

A.

(1;2;3)
B.

(1;0;3)
C.

(0;2;3)
D.

(1;2;0)

Phương pháp giải

Tọa độ của vecto \(\overrightarrow {OA} \) là tọa độ của A.

Lời giải của GV Loigiaihay.com

\(\overrightarrow {OA} = (1;2;3)\).

Đáp án : A

Báo lỗi - Góp ý

BÌNH LUẬN

Danh sách bình luận

Đang tải bình luận...

Các bài tập cùng chuyên đề

Bài 1 :

Để theo dõi hành trình của một chiếc máy bay, ta có thể lập hệ tọa độ Oxyz có gốc O trùng với vị trí của trung tâm kiểm soát không lưu, mặt phẳng (Oxy) trùng với mặt đất (được coi là mặt phẳng) với trục Ox hướng về phía tây, trục Oy hướng về phía nam và trục Oz hướng lên trên trời (H.2.43). Sau khi cất cánh và đạt độ cao nhất định, chiếc máy bay duy trì hướng bay về phía nam với tốc độ không đổi là 890km/h trong nửa giờ. Xác định tọa độ của vectơ biểu diễn độ dịch chuyển của chiếc máy bay trong nửa giờ đó với hệ tọa độ đã chọn, biết rằng đơn vị đo trong không gian Oxyz được lấy theo kilômét.

Xem lời giải >>

Bài 2 :

Trong Ví dụ 5, xác định tọa độ của các điểm D và D’ sao cho ABCD.A’B’C’D’ là hình hộp.

Xem lời giải >>

Bài 3 :

Trong không gian Oxyz, cho hai điểm \(M\left( {x;{\rm{ }}y;{\rm{ }}z} \right)\) và \(N\left( {x';y';z'} \right)\).

a) Hãy biểu diễn hai vectơ \(\overrightarrow {OM} \) và \(\overrightarrow {ON} \) qua các vectơ \(\overrightarrow i ,\overrightarrow j \) và \(\overrightarrow k \).

b) Xác định tọa độ của vectơ \(\overrightarrow {MN} \).

Xem lời giải >>

Bài 4 :

Trong không gian Oxyz, hãy xác định tọa độ của vectơ \(\overrightarrow i + 2\overrightarrow j + 5\overrightarrow k \).

Xem lời giải >>

Bài 5 :

Trong không gian Oxyz, cho vectơ \(\overrightarrow a \) tùy ý (H.2.41). Lấy điểm M sao cho \(\overrightarrow {OM} = \overrightarrow a \) và giải thích vì sao có bộ ba số (x; y; z) sao cho \(\overrightarrow a = x\overrightarrow i + y\overrightarrow j + z\overrightarrow k \).

Xem lời giải >>

Bài 6 :

Trong tính huống mở đầu, hãy chọn một hệ tọa độ phù hợp và xác định tọa độ của chiếc bóng đèn với hệ tọa độ đó.

Trong Hình 2.34, một chiếc bóng đèn cách sàn nhà là 2m, cách hai bức tường lần lượt là 1m và 1,5m.

Xem lời giải >>

Bài 7 :

Trong Ví dụ 3, hãy xác định tọa độ của các điểm B, D và C’.

Xem lời giải >>

Bài 8 :

Tìm tọa độ của điểm N trong Hình 2.39.

Xem lời giải >>

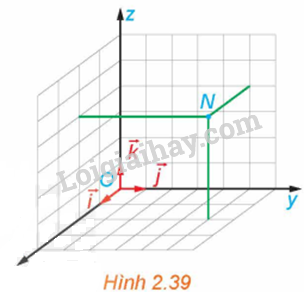
Bài 9 :

Trong không gian Oxyz, xác định tọa độ của vectơ \(\overrightarrow {AB} \) trong mỗi trường hợp sau:
a) \(A\left( {0;0;0} \right)\) và \(B\left( {4;2; - 5} \right)\);
b) \(A\left( {1; - 3;7} \right)\) và \(B\left( {1; - 3;7} \right)\);
c) \(A\left( {5;4;9} \right)\) và \(B\left( { - 5;7;2} \right)\).

Xem lời giải >>

Bài 10 :

Trong không gian Oxyz, xác định tọa độ của điểm A trong mỗi trường hợp sau:
a) A trùng với gốc tọa độ;
b) A nằm trên tia Ox và \(OA = 2\);
c) A nằm trên tia đối của tia Oy và \(OA = 3\).

Xem lời giải >>

Bài 11 :

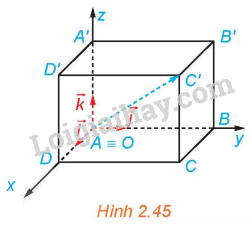
Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có đỉnh A trùng với gốc O và các đỉnh D, B, A’ có tọa độ lần lượt là (2; 0; 0), (0; 4; 0), (0; 0; 3) (H.2.45). Xác định tọa độ của các đỉnh còn lại của hình hộp chữ nhật.

Xem lời giải >>

Bài 12 :

Trong không gian Oxyz, cho hình hộp OABC.O’A’B’C’ có \(A\left( {1;1; - 1} \right),B\left( {0;3;0} \right),C'\left( {2; - 3;6} \right)\).

a) Xác định tọa độ của điểm C.

b) Xác định các tọa độ đỉnh còn lại của hình hộp.

Xem lời giải >>

Bài 13 :

Trong không gian Oxyz, cho hai vectơ \(\overrightarrow a = \left( {1;0;5} \right)\) và \(\overrightarrow b = \left( {1;3;9} \right)\).

a) Biểu diễn hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) qua các vectơ đơn vị \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \).

b) Biểu diễn hai vectơ \(\overrightarrow a + \overrightarrow b \) và \(2\overrightarrow a \) qua các vectơ đơn vị \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \), từ đó xác định tọa độ của hai vectơ đó.

Xem lời giải >>

Bài 14 :

Trong Ví dụ 7, khinh khí cầu thứ nhất hay thứ hai ở xa điểm xuất phát hơn? Giải thích vì sao.

Xem lời giải >>

Bài 15 :

Trong tình huống mở đầu, hãy tính độ lớn của góc \(\alpha \).

Xem lời giải >>

Bài 16 :

Với các giả thiết như trong Ví dụ 5, hãy xác định tọa độ của các chiếc máy bay sau 10 phút tiếp theo (tính từ thời điểm máy bay ở điểm B).

Xem lời giải >>

Bài 17 :

Trong không gian Oxyz, cho hình bình hành ABCD có \(A\left( { - 1;0;3} \right),B\left( {2;1; - 1} \right)\) và \(C\left( {3;2;2} \right)\). Tọa độ của điểm D là
A. \(\left( {2; - 1;0} \right)\).
B. \(\left( {0; - 1; - 6} \right)\).
C. \(\left( {0;1;6} \right)\).
D. \(\left( { - 2;1;0} \right)\).

Xem lời giải >>

Bài 18 :

Trong không gian Oxyz, cho hình hộp OABC.O’A’B’C’ và các điểm \(A\left( {2;3;1} \right),C\left( { - 1;2;3} \right)\) và \(O'\left( {1; - 2;2} \right)\). Tìm tọa độ các đỉnh còn lại của hình hộp.

Xem lời giải >>

Bài 19 :

Hình 2.53 minh họa một chiếc đèn được treo cách trần nhà 0,5m, cách hai tường lần lượt là 1,2m và 1,6m. Hai bức tường vuông góc với nhau và cùng vuông góc với trần nhà. Người ta di chuyển chiếc đèn đó đến vị trí mới cách trần nhà là 0,4m, cách hai tường đều là 1,5m.
a) Lập một hệ trục tọa độ Oxyz phù hợp và xác định tọa độ của bóng đèn lúc đầu và sau khi di chuyển.
b) Vị trí mới của bóng đèn cách vị trí ban đầu là bao nhiêu mét? (Làm tròn kết quả đến chữ số thập phân thứ nhất).

Xem lời giải >>

Bài 20 :

Trong không gian Oxyz, cho các điểm \(A\left( {4;2; - 1} \right),B\left( {1; - 1;2} \right)\) và \(C\left( {0; - 2;3} \right)\).
a) Tìm tọa độ của vectơ \(\overrightarrow {AB} \) và tính độ dài đoạn thẳng AB.
b) Tìm tọa độ điểm M sao cho \(\overrightarrow {AB} + \overrightarrow {CM} = \overrightarrow 0 \).
c) Tìm tọa độ điểm N thuộc mặt phẳng (Oxy), sao cho A, B, N thẳng hàng.

Xem lời giải >>

Bài 21 :

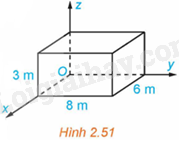
Một phòng học có thiết kế dạng hình hộp chữ nhật với chiều dài là 8m, chiều rộng là 6m và chiều cao là 3m. Một chiếc đèn được treo tại chính giữa trần nhà của phòng học. Xét hệ trục tọa độ Oxyz có gốc O trùng với một góc phòng và mặt phẳng (Oxy) trùng với mặt sàn, đơn vị đo được lấy theo mét (H.2.51). Hãy tìm tọa độ của điểm treo đèn.

Xem lời giải >>

Bài 22 :

Trong không gian, xét hệ tọa độ Oxyz có gốc O trùng với vị trí của một giàn khoan trên biển, mặt phẳng (Oxy) trùng với mặt biển (được coi là phẳng) với trục Ox hướng về phía tây, trục Oy hướng về phía nam và trục Oz hướng thẳng đứng lên trời (H.2.52). Đơn vị đo trong không gian Oxyz lấy theo kilômét. Một chiếc ra đa đặt tại giàn khoan có phạm vi theo dõi là 30km. Hỏi ra đa có thể phát hiện được một chiếc tàu thám hiểm có tọa độ là (25; 15; -10) đối với hệ tọa độ nói trên hay không? Hãy giải thích vì sao.

Xem lời giải >>

Bài 23 :

Trong không gian hãy vẽ:

a, Ba trục số Ox,Oy,Oz vuông góc với nhau từng đôi một và cắt nhau tại gốc O của mỗi trục

b,

- Vecto \(\vec i\;\)xuất phát từ điểm gốc O, theo chiều Ox và có độ dài bằng 1

- Vecto \(\vec j\;\)xuất phát từ điểm gốc O, theo chiều Oy và có độ dài bằng 1

- Vecto \(\vec k\;\)xuất phát từ điểm gốc O, theo chiều Oz và có độ dài bằng 1

Xem lời giải >>

Bài 24 :

Cho điểm M trong không gian với hệ tọa độ Oxyz. Gọi là hình chiếu của điểm M trên mặt phẳng Oxy( hình 22)

a) Trong mặt phẳng Oxy hãy cho biết :

Hình chiếu H của điểm M trên trục hoành Ox ứng với số nào trên trục Ox

Hình chiếu K của điểm M trên trục tung Oy ứng với số nào trên trục Oy

b) Hình chiếu P của điểm M trên trục cao Oz tương ứng với số nào trên trục Oz?

Xem lời giải >>

Bài 25 :

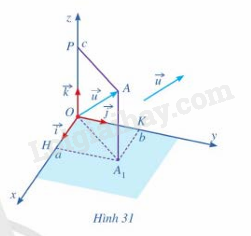
Trong không gian với hệ tọa độ Oxyz, cho vecto \(\vec u = \left( {a;b;c} \right)\)( hình 31)

Lấy điểm A sao cho \(\overrightarrow {OA} = \vec u\).

a) Tìm hoành độ, tung độ và cao độ của điểm A

b) Biểu diễn vecto \(\overrightarrow {OH} \) qua vecto\(\;\vec i\) vecto \(\overrightarrow {OK} \) qua vecto \(\vec j\) ,vecto \(\overrightarrow {OP} \)qua vecto \(\vec k\)

c) Biểu diễn vecto \(\vec u\;\)theo các vecto \(\vec i,\vec j,\vec k\)

Xem lời giải >>

Bài 26 :

Trong không gian với hệ tọa độ Oxyz, cho vecto \(\vec u\;\)(hình 28). Hãy xác định điểm A sao cho \(\overrightarrow {OA} = \vec u\)

Xem lời giải >>

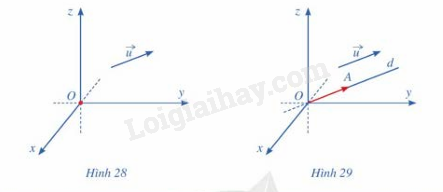
Bài 27 :

Cho điểm M trong không gian với hệ tọa độ Oxyz

a) Vẽ vecto \(\overrightarrow {OM} \)

b) Nêu cách xác định tọa độ của điểm M

Xem lời giải >>

Bài 28 :

Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B})\)

a.Biểu diễn mỗi vecto \(\overrightarrow {OA} ,\overrightarrow {OB} \) theo các vecto \(\overrightarrow i ,\overrightarrow j \) và \(\overrightarrow k \)

b. Tìm liên hệ giữa \(\overrightarrow {AB} \) và \(({x_B} - {x_A}).\vec i + ({y_B} - {y_A}).\vec j + ({z_B} - {z_A}).\vec k\)

c. Từ đó, tìm tọa độ vecto \(\overrightarrow {AB} \)

Xem lời giải >>

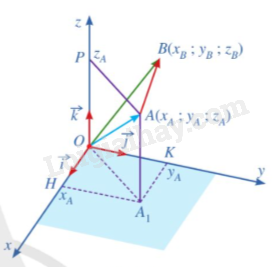
Bài 29 :

Trong không gian với hệ tọa độ \(Oxyz\), cho \(A\left( {3; - 2; - 1} \right)\). Gọi \({A_1},{A_2},{A_3}\) lần lượt là hình chiếu của điểm \(A\) trên các mặt phẳng tọa độ \(\left( {Oxy} \right),\left( {Oyz} \right),\left( {Ozx} \right)\). Tìm tọa độ của các điểm \({A_1},{A_2},{A_3}\).

Xem lời giải >>

Bài 30 :

Trong không gian với hệ tọa độ \(Oxyz\), cho \(A\left( { - 2;3;4} \right)\). Gọi \(H,K,P\) lần lượt là hình chiếu của điểm \(A\) trên các trục \(Ox,Oy,Oz\). Tìm tọa độ của các điểm \(H,K,P\).

Xem lời giải >>