Đề bài

Một con lắc lò xo treo thẳng đứng với biên độ \(8cm\). Khoảng thời gian từ lúc lực đàn hồi cực đại đến lúc lực đàn hồi cực tiểu là \(\dfrac{T}{3}\), với \(T\) là chu kì dao động của con lắc. Tốc độ của vật nặng khi nó cách vị trí thấp nhất \(2cm\). Lấy\(g = {\pi ^2}\left( {m/{s^2}} \right)\).

• A. \(83,11 cm/s\)
• B. \(106,45cm/s\)
• C. \(87,66cm/s\)
• D. \(57,37cm/s\)

Phương pháp giải

+ Xác định vị trí lực đàn hồi cực đại, cực tiểu của con lắc lò xo treo thẳng đứng

+ Áp dụng biểu thức xác định độ dãn của lò xo treo thẳng đứng tại vị trí cân bằng: \(\Delta l = \dfrac{{mg}}{k}\)

+ Sử dụng hệ thức độc lập A-x-v:

\({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}\)                  

Lời giải của GV Loigiaihay.com

Chọn chiều dương hướng xuống

Vị trí lực đàn hồi cực đại: \(x = + A\)

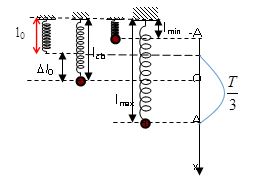
Ta có thời gian từ lúc lực đàn hồi cực đại đến lúc lực đàn hồi cực tiểu là \(\dfrac{T}{3}\)

=> Ta có góc quét: \(\Delta \varphi  = \omega \Delta T = \dfrac{{2\pi }}{T}.\dfrac{T}{3} = \dfrac{{2\pi }}{3}\), vẽ trên vòng tròn lượng giác, ta được:

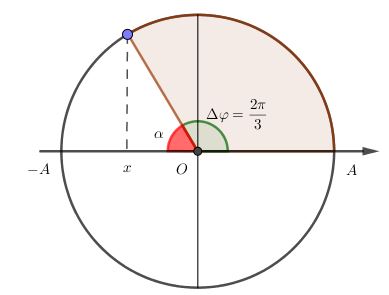
Ta có góc \(\alpha  = \pi  - \dfrac{{2\pi }}{3} = \dfrac{\pi }{3}\)

=> vị trí lực đàn hồi cực tiểu là \(x =  - \Delta l =  - Acos\alpha  =  - Acos\dfrac{\pi }{3} =  - \dfrac{A}{2} =  - 4cm\)

\( \to \Delta l = \dfrac{{mg}}{k} = \dfrac{{mg}}{{m{\omega ^2}}} = 0,04 \to \omega  = \sqrt {\dfrac{g}{{0,04}}}  = 5\pi (ra{\rm{d}}/s)\)

- Vị trí cách vị trí thấp nhất \(2cm\) có li độ: \(x{\rm{ }} = {\rm{ }}6cm\)

 \({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} \leftrightarrow {8^2} = {6^2} + \dfrac{{{v^2}}}{{{{\left( {5\pi } \right)}^2}}} \to v =  \pm 10\sqrt 7 \pi cm/s\)

Đáp án : A