Hàm số nào dưới đây không liên tục trên \(\mathbb{R}\)?
A. \(y = \tan x\).
B. \(y = \frac{{2{x^2} + 3x - 1}}{{{x^2} + 1}}\).
C. \(y = \sin x\).
D. \(y = |x|\).
Hàm số sơ cấp liên tục trên tập xác định của chúng.
TXĐ của \(y = \tan x\) là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi } \right\}\).
Đáp án A

Các bài tập cùng chuyên đề
Bài 1 :
Tìm \(m\) để các hàm số \(f(x) = \left\{ \begin{array}{l}\frac{{\sqrt[3]{{x - 2}} + 2x - 1}}{{x - 1}}{\rm{ khi }}x \ne 1\\3m - 2{\rm{ khi }}x = 1\end{array} \right.\) liên tục trên \(\mathbb{R}\).
-
A.
\(m = \frac{13}{9}\)
-
B.
\(m = \frac{5}{3}\)
-
C.
\(m = \frac{3}{4}\)
-
D.
\(m = 0\)
Bài 2 :
Tìm các khoảng trên đó hàm số \(f\left( x \right) = \frac{{{x^2} + 1}}{{x + 2}}\) liên tục.
Bài 3 :
Cho hai hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{2x\;,\;0 \le x \le \frac{1}{2}}\\{1\;,\frac{1}{2} < x \le 1}\end{array}} \right.\) và \(g\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{x\;,0 \le x \le \frac{1}{2}}\\{1\;,\frac{1}{2} < x \le 1}\end{array}} \right.\)với đồ thị tương ứng như Hình 5.7

Xét tính liên tục của các hàm số f(x) và g(x) tại điểm \(x = \frac{1}{2}\)và nhận xét về sự khác nhau giữa hai đồ thị.
Bài 4 :
Xét tính liên tục của các hàm số sau trên tập xác định của chúng:
a) \(f\left( x \right) = \frac{x}{{{x^2} + 5x + 6}}\)
b) \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{1 + {x^2}\;,\;x < 1}\\{4 - x\;\;,\;x \ge 1}\end{array}} \right.\)
Bài 5 :
Cho hàm số \(f\left( x \right) = \frac{{x + 1}}{{\left| {x + 1} \right|}}\). Hàm só \(f\left( x \right)\) liên tục trên
A. \(\left( { - \infty ;\; + \infty } \right)\)
B. \(\left( { - \infty ;\; - 1} \right]\)
C. \(\left( { - \infty ;\; - 1} \right) \cup \left( { - 1;\; + \infty } \right)\)
D. \(\left[ { - 1;\; + \infty } \right)\)
Bài 6 :
Tìm tập xác định của các hàm số sau và giải thích tại sao các hàm này liên tục trên các khoảng xác định của chúng
a) \(f\left( x \right) = \frac{{\cos x}}{{{x^2} + 5x + 6}}\);
b) \(g\left( x \right) = \frac{{x - 2}}{{\sin x}}\)
Bài 7 :
Lực hấp dẫn tác dụng lên một đơn vị khối lượng ở khoảng cách r tính từ tâm Trái Đất là
\(F\left( r \right) = \left\{ {\begin{array}{*{20}{c}}{\frac{{GMr}}{{{R^3}}}\;,r < R}\\{\frac{{GM}}{{{r^2}}}\;,\;r \ge R}\end{array}} \right.\)
Trong đó M và R lần lượt là khối lượng và bán kính của Trái Đất, G là hằng số hấp dẫn. Xét tính liên tục của hàm số F(r).
Bài 8 :
Hàm số \(f\left( x \right) = \left\{ \begin{array}{l}x - 1,\,\,x < 2\\ - x,\,\,x \ge 2\end{array} \right.\) có liên tục trên \(\mathbb{R}\) hay không?
Bài 9 :
Cho hàm số \(f\left( x \right) = x + 1\) với \(x \in \mathbb{R}.\)
a) Giả sử \({x_0} \in \mathbb{R}.\) Hàm số \(f\left( x \right)\) có liên tục tại điểm \({x_0}\) hay không?
b) Quan sát đồ thị hàm số \(f\left( x \right) = x + 1\) với \(x \in \mathbb{R}\) (Hình 13), nếu nhận xét về đặc điểm của đồ thị hàm số đó.
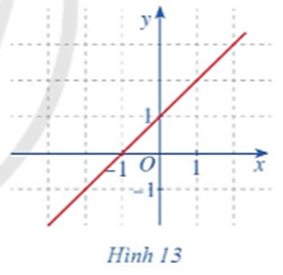
Bài 10 :
Trong các hàm số có đồ thị ở Hình 15a, 15b, 15c, hàm số nào liên tục trên tập xác định của hàm số đó? Giải thích.
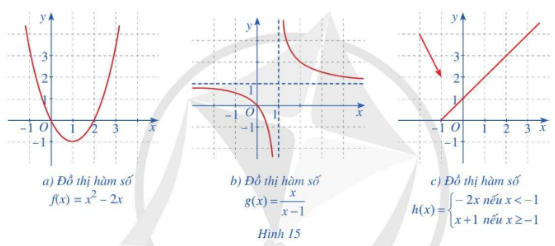
Bài 11 :
Xét tính liên tục của mỗi hàm số sau trên tập xác định của hàm số đó:
a) \(f\left( x \right) = {x^2} + \sin x;\)
b) \(g\left( x \right) = {x^4} - {x^2} + \frac{6}{{x - 1}};\)
c) \(h\left( x \right) = \frac{{2x}}{{x - 3}} + \frac{{x - 1}}{{x + 4}}.\)
Bài 12 :
Tại một xưởng sản xuất bột đã thạch anh, giá bán (tính theo nghìn đồng) của \(x\) (kg) bột đã thạch anh được tính theo công thức sau:
\(P\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{4,5x}&{khi\,\,0 < x \le 400}\\{4x + k}&{khi\,\,x > 400}\end{array}} \right.\) (\(k\) là một hãng số).
a) Với \(k = 0\), xét tính liên tục của hàm số \(P\left( x \right)\) trên \(\left( {0; + \infty } \right)\).
b) Với giá trị nào của \(k\) thì hàm số \(P\left( x \right)\) liên tục trên \(\left( {0; + \infty } \right)\)?
Bài 13 :
Xét tính liên tục của hàm số \(y = \sqrt {x - 1} + \sqrt {2 - x} \) trên \(\left[ {1;2} \right]\).
Bài 14 :
Cho hàm số \(y = f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{x + 1}&{khi\,\,1 < x \le 2}\\k&{khi\,\,x = 1}\end{array}} \right.\).
a) Xét tính liên tục của hàm số tại mỗi điểm \({x_0} \in \left( {1;2} \right)\).
b) Tìm \(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right)\) và so sánh giá trị này với \(f\left( 2 \right)\).
c) Với giá trị nào của \(k\) thì \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = k\)?
Bài 15 :
Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{\frac{{{x^2} - 4}}{{x + 2}}}&{khi\,\,x \ne - 2}\\a&{khi\,\,x = - 2}\end{array}} \right.\).
Tìm \(a\) để hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\).
Bài 16 :
Xét tính liên tục của các hàm số sau:
a) \(f\left( x \right) = \frac{x}{{{x^2} - 4}}\);
b) \(g\left( x \right) = \sqrt {9 - {x^2}} \);
c) \(h\left( x \right) = \cos x + \tan x\).
Bài 17 :
Xét tính liên tục của hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{\sqrt {x + 4} }&{khi\,\,x \ge 0}\\{2\cos x}&{khi\,\,x < 0}\end{array}} \right.\).
Bài 18 :
Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{\frac{{{x^2} - 25}}{{x - 5}}}&{khi\,\,x \ne 5}\\a&{khi\,\,x = 5}\end{array}} \right.\).
Tìm \(a\) để hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\).
Bài 19 :
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\tan x\;\;\;\;\;\;\,khi\;0 < x \le \frac{\pi }{4}\\k - \cot x\;\,khi\;\frac{\pi }{4} < x \le \frac{\pi }{2}\end{array} \right.\) liên tục tại trên đoạn \(\left[ {0;\frac{\pi }{2}} \right]\). Giá trị của k bằng
A. 0.
B. 1.
C. 2.
D. \(\frac{\pi }{2}\).
Bài 20 :
Hàm số \(y = f\left( x \right)\) liên tục trên khoảng:
A. \(\left( { - \infty ;1} \right)\)
B. \(\left( { - \infty ; + \infty } \right)\)
C. \(\left( {1; + \infty } \right)\)
D. \(\left( { - \infty ;2} \right)\)
Bài 21 :
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}3\;\;\;\;\;\;\;\;\;khi\;x \le 1\\ax + b\;\;khi\;1 < x < 2\\5\;\;\;\;\;\;\;\;\;khi\;x \ge 2\end{array} \right.\). Xác định a, b để hàm số liên tục trên \(\mathbb{R}\).
Bài 22 :
Tìm tham số m để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} - 1}}{{x - 1}}\;\;\;khi\;x < 1\\mx + 1\;\;khi\;x \ge 1\end{array} \right.\) liên tục trên \(\mathbb{R}\).
Bài 23 :
Xét tính liên tục của các hàm số sau trên tập xác định của chúng:
a) \(f\left( x \right) = \frac{{{x^3} + x + 1}}{{{x^2} - 3x + 2}}\)
b) \(f\left( x \right) = \frac{{\cos x}}{{{x^2} + 3x - 4}}\)
Bài 24 :
Cho hàm số \(f(x) = \left\{ \begin{array}{l}2\,\,\,{\rm{khi}}\,\,\, - 1 < x \le 1\\1 - x\,\,{\rm{khi}}\,\,x \le - 1\,\,{\rm{hay}}\,\,x > 1\end{array} \right.\). Mệnh đề đúng là
A. Hàm số \(f(x)\) liên tục trên \([ - 1;\,1]\)
B. Hàm số \(f(x)\) liên tục trên \(( - 1;\,1]\)
C. Hàm số \(f(x)\) liên tục trên \([ - 1;\,1)\)
D. Hàm số \(f(x)\) liên tục trên \(\mathbb{R}\).
Bài 25 :
Xét hàm số \(f(x) = \left\{ \begin{array}{l}\frac{{{x^2} + 3x + 2}}{{x + 1}}\,\,{\rm{khi}}\,\,x \ne - 1\\m\,\,{\rm{khi}}\,\,\,x = - 1\end{array} \right.\) với m là tham số. Hàm số \(f(x)\) liên tục trên \(\mathbb{R}\) khi
A. \(m = 0\)
B.\(m = 3\)
C.\(m = - 1\)
D.\(m = 1\).
Bài 26 :
Cho hàm số \(f(x) = \frac{{x(x - 1)}}{{\sqrt {x - 1} }}\). Hàm số này liên tục trên
A.\(\left( {1; + \infty } \right)\)
B.\(\left( { - \infty ;1} \right)\)
C. \([1; + \infty )\)
D. \(( - \infty ;1]\).
Bài 27 :
Cho các hàm số \(y = \cos x\,\left( I \right)\), \(y = \sin \sqrt x \,\left( {II} \right)\) và \(y = \tan x\,\left( {III} \right)\). Hàm số nào liên tục trên \(\mathbb{R}\)?
-
A.
\(\left( I \right),\,\left( {II} \right)\).
-
B.
\(\left( I \right)\).
-
C.
\(\left( I \right),\,\left( {II} \right),\,\left( {III} \right)\).
-
D.
\(\left( {III} \right)\).
Bài 28 :
Tìm khẳng định đúng trong các khẳng định sau:
I. \(f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và \(f\left( a \right) \cdot f\left( b \right) < 0\) thì phương trình \(f\left( x \right) = 0\) có nghiệm.
II. \(f\left( x \right)\) không liên tục trên \(\left[ {a;b} \right]\) và \(f\left( a \right) \cdot f\left( b \right) \ge 0\) thì phương trình \(f\left( x \right) = 0\) vô nghiệm.
-
A.
Chỉ I đúng.
-
B.
Chỉ II đúng.
-
C.
Cả I và II đúng.
-
D.
Cả I và II sai.
Bài 29 :
Hàm số nào sau đây liên tục trên \(\mathbb{R}?\)
-
A.
\(y = {x^3} - 3x + 1.\)
-
B.
\(y = \sqrt {x - 4} .\)
-
C.
\(y = \tan x.\)
-
D.
\(y = \sqrt x .\)
Bài 30 :
Hàm số nào sau đây liên tục trên $\mathbb{R}$?
-
A.
$y = \sqrt x .$
-
B.
$y = \cot x.$
-
C.
$y = \tan x.$
-
D.
$y = \frac{1}{{{x^2} + 1}}.$


















Danh sách bình luận