Cho tam giác \(ABC\) có \(BC=15 cm, CA=18 cm\) và \(AB=12 cm\). Gọi \(I\) và \(G\) lần lượt là giao điểm ba đường phân giác và trọng tâm \(\Delta ABC\).
a) Tính độ dài các đoạn thẳng \(CD\) và \(BD\).
b) Chứng minh \(IG\parallel BC\).
c) Tính độ dài đoạn thẳng \(IG\).
- Vẽ hình theo yêu cầu của bài toán.
a) Gọi \(AD\) là đường phân giác góc \(BAC\,\left( {D \in BC} \right)\).
Chứng minh \(\frac{{DC}}{{AC}} = \frac{{DB}}{{AB}}\) và áp dụng tính chất dãy tỉ số bằng nhau để tính \(CD\)
b) Chứng minh \(\frac{{AI}}{{DI}} = \frac{{AG}}{{GM}} = 2\). Vậy theo định lí Thales đảo ta suy ra được \(IG\parallel BC\).
c) Gọi \(M\) là trung điểm của \(BC\).
Xét \(\Delta ADM\) có \(IG\parallel BC\), theo hệ quả định lí Thales ta có \(\frac{{IG}}{{DM}} = \frac{{AG}}{{AM}}\).
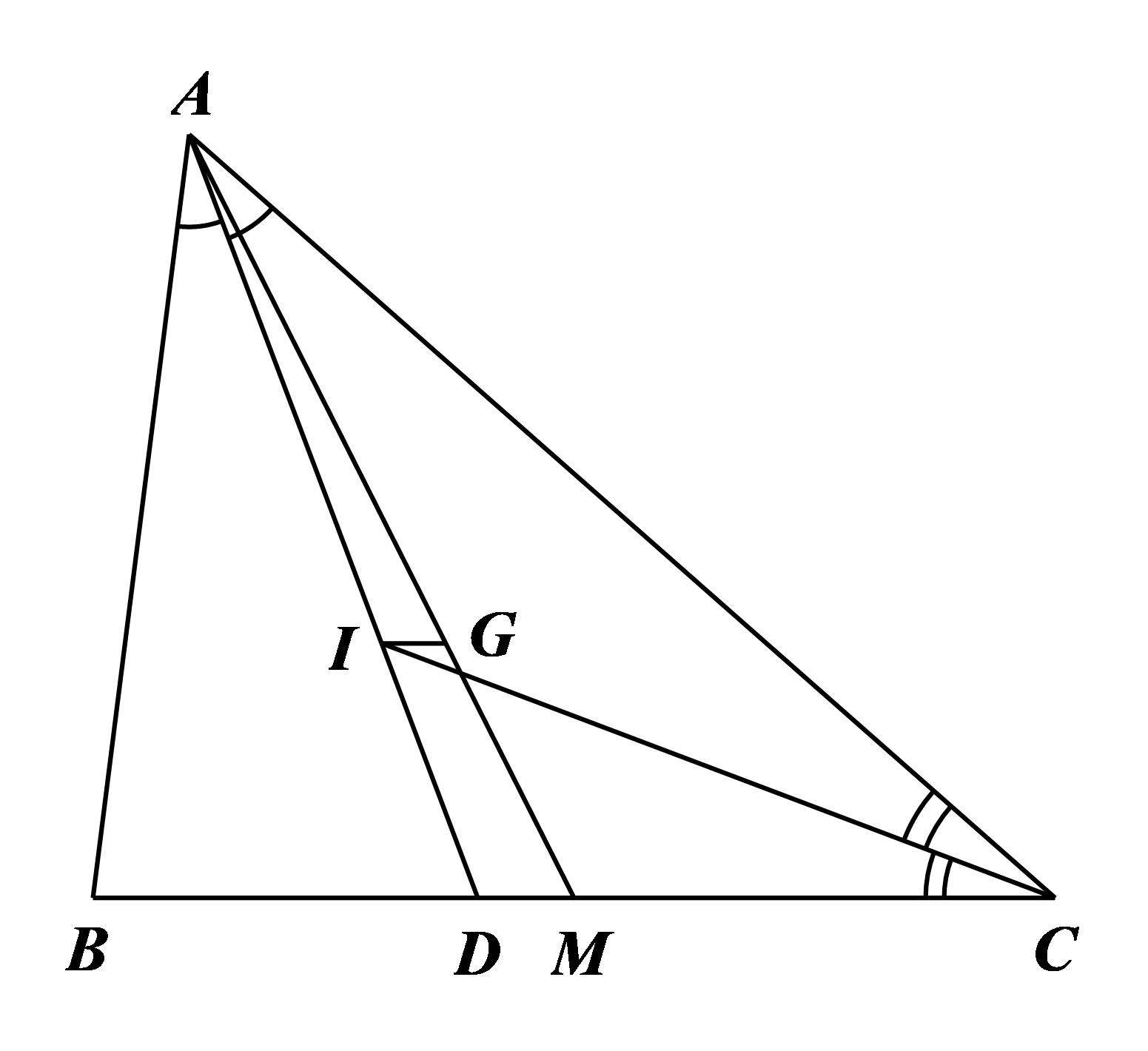
a) Gọi \(AD\) là đường phân giác góc \(BAC\,\left( {D \in BC} \right)\).
Xét \(\Delta ABC\) có \(AD\) là đường phân giác của \(\widehat {BAC}\) nên \(\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}}\), hay \(\frac{{DC}}{{AC}} = \frac{{DB}}{{AB}}\).
Theo tính chất dãy tỉ số bằng nhau ta có:
\(\frac{{DC}}{{AC}} = \frac{{DB}}{{AB}} = \frac{{DC + DB}}{{AC + AB}} = \frac{{BC}}{{AC + AB}} = \frac{{15}}{{18 + 12}} = \frac{1}{2}\)
Suy ra \(CD = \frac{1}{2}AC = \frac{1}{2}.12 = 6\,cm\).
b) Xét \(\Delta ACD\), có \(CI\) là đường phân giác của \(\widehat {ACD}\) nên \(\frac{{AI}}{{DI}} = \frac{{AC}}{{DC}} = \frac{{12}}{6} = 2\) (Tính chất tia phân giác trong tam giác)
Mặt khác, do \(G\) là trọng tâm của \(\Delta ABC\) nên \(\frac{{AG}}{{GM}} = 2\).
Do đó \(\frac{{AI}}{{DI}} = \frac{{AG}}{{GM}} = 2\), theo định lí Thales đảo ta có \(IG\parallel BC\).
c) Gọi \(M\) là trung điểm của \(BC\). Khi đó \(MB = MC = \frac{1}{2}BC = \frac{1}{2}.15 = 7,5\,cm\)
Suy ra \(DM = BM - BD = 7,5 - 6 = 1,5\,cm\).
Xét \(\Delta ADM\) có \(IG\parallel BC\), theo hệ quả định lí Thales ta có \(\frac{{IG}}{{DM}} = \frac{{AG}}{{AM}} = \frac{2}{3}\).
Suy ra \(IG = \frac{2}{3}DM = \frac{2}{3}.1,5 = 1\,cm\).

Các bài tập cùng chuyên đề
Bài 1 :
Cho hình vẽ, biết \(DE// BC\). Khẳng định nào sau đây là đúng?
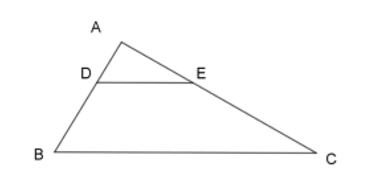
-
A.
\(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}\)
-
B.
\(AD.AE = AB.AC\)
-
C.
\(\dfrac{{AD}}{{DB}} = \dfrac{{DE}}{{BC}}\)
-
D.
\(DE.AD = AB.BC\)
Bài 2 :
Bạn An đo được khoảng cách từ vị trí mình đứng (điểm K) đến cây D và cây E ở hai bên hồ nước lần lượt là KD = 18m và KE = 20,25m. Để tính độ dài DE, An xác định điểm A nằm giữa K, D và điểm E nằm giữa K, E sao cho KA = 6,4m, KB = 7,2m và khoảng cách giữa A và B là 32m.
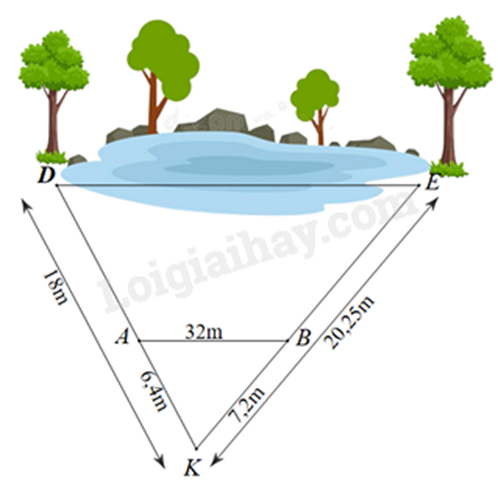
a) Chứng minh \(\frac{{KB}}{{KE}} = \frac{{AK}}{{KD}}\).
b) Chứng minh \(AB//DE\).
c) Tính khoảng cách giữa D và E.
Bài 3 :
Cho tam giác ABC vuông tại A. Gọi D, E, F lần lượt là trung điểm của AB, BC, AC.
a) Chứng minh rằng AE = DF.
b) Gọi I là trung điểm của DE. Chứng minh rằng ba điểm B, I, F thẳng hàng.
Bài 4 :
Cho tam giác ABC, phân giác AD (D ∈ BC). Đường thẳng qua D song song với AB cắt AC tại E. Chứng minh rằng \(\dfrac{{AC}}{{AB}} = \dfrac{{EC}}{{E{\rm{A}}}}\)
Bài 5 :
Cho tam giác ABC, điểm I nằm trong tam giác. Lấy điểm D trên IA, qua D kẻ đường thẳng song song với AB, cắt IB tại E. Qua E kẻ đường thẳng song song với BC, cắt IC tại F. Chứng minh rằng: DF//AC
Bài 6 :
Cho hình thang \(ABCD\left( {AB//CD} \right)\). Đường thẳng song song với \(AB\) cắt \(AD, BD, AC\) và \(BC\) theo thứ tự tại các điểm \(M, N, P, Q\).
Chứng minh rằng \(MN = PQ\).
Bài 7 :
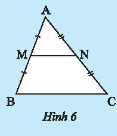
Cho \(M,N\) lần lượt là trung điểm của hai cạnh \(AB;AC\) của tam giác \(ABC\).
a) Tính các tỉ số \(\frac{{AM}}{{AB}},\frac{{AN}}{{AC}}\);
b) Chứng mình \(MN//BC\);
c) Chứng minh \(\frac{{MN}}{{BC}} = \frac{1}{2}\).
Bài 8 :
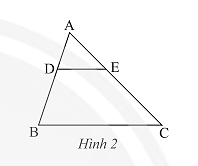
Cho tam giác \(ABC\), biết \(DE//BC\) (Hình 2). Trong các khẳng định sau, khẳng định nào sai?
A. \(\frac{{AD}}{{DB}} = \frac{{AE}}{{EC}}\).
B. \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}\).
C. \(\frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}\).
D. \(\frac{{BD}}{{AB}} = \frac{{DE}}{{BC}}\).
Bài 9 :
Cho \(\Delta ABC\), một đường thẳng song song với \(BC\) cắt \(AB\) và \(AC\) lần lượt tại \(D\) và \(E\). Qua \(E\) kẻ đường thẳng song song với \(CD\) cắt \(AB\) tại \(F\). Biết \(AB = 25cm,AF = 9cm,EF = 12cm\), độ dài đoạn \(DC\) là
A. 25cm.
B. 20cm.
C. 15cm.
D. 12cm.
Bài 10 :
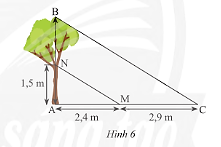
a) Độ cao \(AN\) và chiều dài bóng nắng của các đoạn thẳng \(AN,BN\) trên mặt đất được ghi lại như trong Hình 6. Tính chiều cao \(AB\)của cái cây.
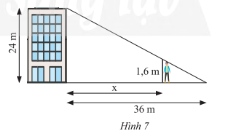
b) Một tòa nhà cao 24m, đổ bóng nắng dài 36m trên đường như Hình 7. Một người cao 1,6m muốn đứng trong bóng dâm của toàn nhà. Hỏi người đó có thể đứng cách tòa nhà xa nhất là bao nhiêu mét?
Bài 11 :
Cho tam giác \(ABC\) có \(BC\) bằng 30cm. Trên đường cao \(AH\) lấy các điểm \(K,I\) sao cho \(AK = KI = IH\). Qua \(I\) và \(K\) vẽ các đường \(EF//BC,MN//BC\left( {E,M \in AB;F,N \in AC} \right)\).
a) Tính độ dài các đoạn thẳng \(MN\) và \(EF\).
b) Tính diện tích tứ giác \(MNFE\) biết rằng diện tích tam giác \(ABC\) là \(10,8d{m^2}\).
Bài 12 :
Cho tứ giác \(ABCD\) có \(AC\) và \(BD\) cắt nhau tại . Qua \(O\), kẻ đường thẳng song song với \(BC\) cắt \(AB\) tại \(E\), kẻ đường thẳng song song với \(CD\) cắt \(AD\) tại \(F\).
a) Chứng minh: \(EF//BD\);
b) Từ \(O\) kẻ đường thẳng song song với \(AB\) cắt \(BC\) tại \(G\) và đường thẳng song song với \(AD\) cắt \(CD\) tại \(H\). Chứng minh rằng \(CG.DH = BG.CH\).
Bài 13 :
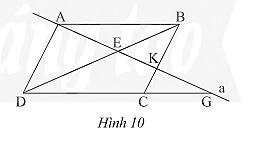
Cho hình bình hành \(ABCD\). Đường thẳng \(a\) đi qua \(A\) cắt \(BD,BC,DC\) lần lượt tại \(E,K,G\) (Hình 10). Chứng minh rằng:
a) \(A{E^2} = EK.EG\);
b) \(\frac{1}{{AE}} = \frac{1}{{AK}} + \frac{1}{{AG}}\).
Bài 14 :
Cho hình thang ABCD \(\left( {AB\parallel CD} \right)\) có AB = 4cm, CD = 6cm. Đường thẳng d song song với hai đáy và cắt hai cạnh bên AD, BC của hình thang đó lần lượt tại M, N; cắt đường chéo AC tại P.
a) Chứng minh \(\frac{{AM}}{{MD}} = \frac{{BN}}{{NC}}\);
b) Tính độ dài các đoạn thẳng MP, PN, MN; biết rằng MD = 2MA.
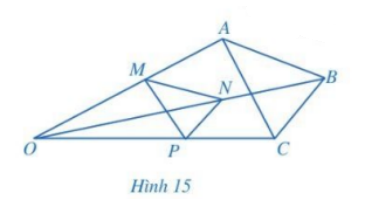
Bài 15 :
Trong Hình 15, cho \(MN\parallel AB,\,\,NP\parallel BC\). Chứng minh \(MP\parallel AC\).
Bài 16 :
Cho tam giác \(ABC\). Điểm \(O\) nằm trong tam giác. Lấy điểm \(D\) trên \(AO\), từ \(D\) kẻ \(DE\parallel AB\) (\(E \in OB\)) và \(DF\parallel AC\) (\(F \in OC\)). Khẳng định nào sau đây là sai?
-
A.
\(\frac{{OF}}{{FC}} = \frac{{OA}}{{OD}}\)
-
B.
\(\frac{{OF}}{{OC}} = \frac{{OD}}{{OA}}\)
-
C.
\(\frac{{OE}}{{OB}} = \frac{{OD}}{{OA}}\)
-
D.
\(EF\parallel BC\)
Bài 17 :
Cho tam giác \(ABC\), \(I\) và \(K\) là hai điểm bất kì trên cạnh \(AB\) và \(AC\). Từ \(I\) kẻ \(IM\parallel BK\) (\(M \in AC\)), từ \(K\) kẻ \(KN\parallel CI\) (\(N \in AB\)). Khi đó \(MN\) …… \(BC\). Từ thích hợp điền vào chỗ chấm là:
-
A.
vuông góc với;
-
B.
song song với;
-
C.
trùng với;
-
D.
cắt.
Bài 18 :
Cho tam giác \(ABC\), đường thẳng \(d\) cắt \(AB,\, AC\) lần lượt tại \(D\) và \(E\) sao cho \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}\). Khẳng định nào sau đây là sai?
-
A.
\(\frac{{AD}}{{DB}} = \frac{{AE}}{{EC}}\)
-
B.
\(\frac{{BD}}{{AB}} = \frac{{CE}}{{AC}}\)
-
C.
\(\frac{{AD}}{{AB}} = \frac{{AE}}{{EC}}\)
-
D.
\(DE\parallel BC\)
Bài 19 :
Cho tam giác ABC vuông tại A (AB < AC), đường cao AH. Gọi E và F lần lượt là hình chiếu vuông góc của H trên AB, AC.
a) Chứng minh tứ giác AEHF là hình chữ nhật.
b) Gọi M là trung điểm của BC. Đường thẳng qua B vuông góc với AB cắt đường thẳng FM ở D. Chứng minh tứ giác BDCF là hình bình hành.
c) Chứng minh BE.AC + CF.AB = AB.AC.
Bài 20 :
Cho tam giác ABC vuông tại A có MN//BC \(\left( {M \in AB,N \in AC} \right)\). Biết \(AB = 9cm,AM = 3cm,AN = 4cm\). Tính độ dài NC, MN, BC.
Bài 21 :
Trong Hình 10, cho biết \(ABCD\) là hình thang, \(AB//CD\left( {AB < CD} \right)\); \(M\) là trung điểm của \(DC\); \(AM\) cắt \(BD\) ở \(I\); \(BM\) cắt \(AC\) ở \(K\); \(IK\) cắt \(AD,BC\) lần lượt ở \(E,F\). Chứng minh:
a) \(IK//AB\)
b) \(EI = IK = KF\)

Bài 22 :
Cho tam giác \(ABC\) vuông tại \(A\), có đường phân giác \(AD\). Vẽ hình vuông \(MNPQ\) ở đó \(M\) thuộc cạnh \(AB,N\) thuộc cạnh \(AC,P\) và \(Q\) thuộc cạnh \(BC\). Gọi \(E\) và \(F\) lần lượt là giao điểm của \(BN\) và \(MQ\); \(CM\) và \(NP\) (Hình 60). Chứng minh:
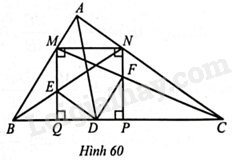
a) \(DE\) song song với \(AC\);
b) \(DE=DF\).
Bài 23 :
Cho tam giác ABC vuông tại A có AB = 6cm. AC = 8cm. M, N là trung điểm của AB , AC. Vẽ AD là tia phân giác của góc A trong tam giác ABC (D thuộc BC).
a) BC = 10cm.
b) MN = 4cm.
c) \(BD \approx 4,5\)cm.
d) \(BD.AN = AM.DC\).


















Danh sách bình luận