Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối tia của tia CB lấy điểm N sao cho BM = CN. Kẻ BE ⊥ AM (E ∈ AM), CF ⊥ AN (F ∈ AN).
EB và FC kéo dài cắt nhau tại O. Chứng minh AO là tia phân giác của góc MAN
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối tia của tia CB lấy điểm N sao cho BM = CN. Kẻ BE ⊥ AM (E ∈ AM), CF ⊥ AN (F ∈ AN).
EB và FC kéo dài cắt nhau tại O. Chứng minh AO là tia phân giác của góc MAN
- Vẽ hình theo yêu cầu bài toán.
- Chứng minh ∆BME = ∆CNF để suy ra AE = AF.
- Chứng minh ∆AEO = ∆AFO. Suy ra \(\widehat {OAE} = \widehat {OAF}\) (hai góc tương ứng).
Vậy AO là tia phân giác của góc MAN.
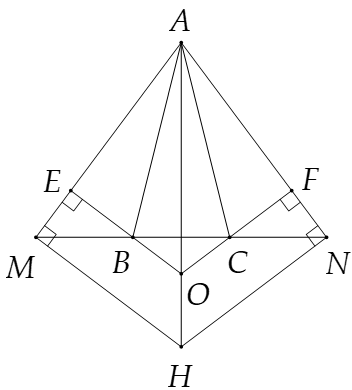
Vì ∆ABC cân tại A nên \(\widehat {ABC} = \widehat {ACB}\) suy ra \(\widehat {ABM} = \widehat {ACN}\).
Xét ∆ABM và ∆ACN có:
AB = AC (vì ∆ABC cân tại A)
\(\widehat {ABM} = \widehat {ACN}\) (chứng minh trên)
BM = CN (giả thiết)
Do đó ∆ABM = ∆ACN (c.g.c).
Suy ra \(\widehat {AMB} = \widehat {ANC}\) (hai góc tương ứng).
Xét ∆BME và ∆CNF có:
\(\widehat {BEM} = \widehat {CFN} = 90^\circ \)
BM = CN (giả thiết)
\(\widehat {AMB} = \widehat {ANC}\) (chứng minh trên)
Do đó ∆BME = ∆CNF (cạnh huyền – góc nhọn).
Suy ra ME = NF (Hai cạnh tương ứng).
Mà AM = AN nên AE = AF.
Ta lại có \(\widehat {EBM} = \widehat {FCN}\) suy ra \(\widehat {OBC} = \widehat {OCB}\).
Do đó ∆OBC cân tại O từ đó OB = OC suy ra OE = OF.
Xét ∆AEO và ∆AFO có:
AE = AF (chứng minh trên)
\(\widehat {AEO} = \widehat {AFO} = 90^\circ \)
OE = OF (chứng minh trên)
Do đó ∆AEO = ∆AFO (c.g.c)
Suy ra \(\widehat {OAE} = \widehat {OAF}\) (hai góc tương ứng).
Vậy AO là tia phân giác của góc MAN.

Các bài tập cùng chuyên đề
Bài 1 :
Mỗi hình sau có các cặp tam giác vuông nào bằng nhau? Vì sao?
Bài 2 :
Cho đoạn thẳng AB, O là trung điểm AB. Trên cùng một nửa mặt phẳng bờ AB vẽ các tia Ax; By vuông góc với AB. Gọi C là một điểm thuộc D. Khi đó:
-
A.
BD = CD + AC
-
B.
AC = DC + BD
-
C.
CD = AC - BD
-
D.
CD = AC + BD
Bài 3 :
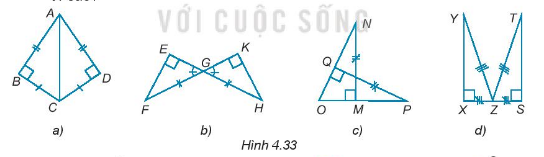
Trong mỗi hình sau (H.4.33) có các cặp tam giác vuông nào bằng nhau? Vì sao?
Bài 4 :
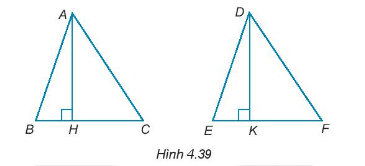
Cho AH và DK lần lượt là hai đường cao của tam giác ABC và DEF như Hình 4.39. Chứng minh rằng
a) Nếu AB = DE, BC = EF và AH = DK thì \(\Delta ABC = \Delta DEF;\)
b) Nếu AB = DE, AC = DF và AH = DK thì \(\Delta ABC = \Delta DEF\)
Bài 5 :
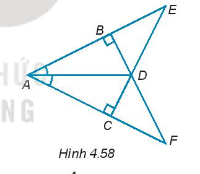
Cho các điểm A, B, C, D, E, F như Hình 4.58.
a) Tìm ba cặp tam giác vuông bằng nhau và giải thích vì sao chúng bằng nhau.
b) Chứng minh \(\Delta ADE = \Delta ADF\).
Bài 6 :
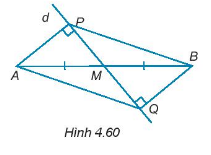
Cho đường thẳng d đi qua trung điểm M của đoạn thẳng AB và không vuông góc với AB. Kẻ AP, BQ \(\left( {P \in d,Q \in d} \right)\) vuông góc với đường thẳng d (H 4.60). Chứng minh rằng:
a) AP = BQ
b) \(\Delta APB = \Delta BQA\).
Bài 7 :
Hai tam giác vuông bằng nhau khi và chỉ khi điều nào dưới đây xảy ra?
A. Một cạnh góc vuông và một góc nhọn của tam giác này bằng một cạnh góc vuông và một góc nhọn của tam giác kia.
B. Một cạnh góc vuông và góc nhọn kề cạnh ấy của tam giác này bằng một cạnh góc vuông và góc nhọn kề cạnh ấy của tam giác kia.
C. Hai góc nhọn của tam giác này bằng hai góc nhọn của tam giác kia.
D. Hai cạnh của tam giác này bằng hai cạnh của tam giác kia.
Bài 8 :
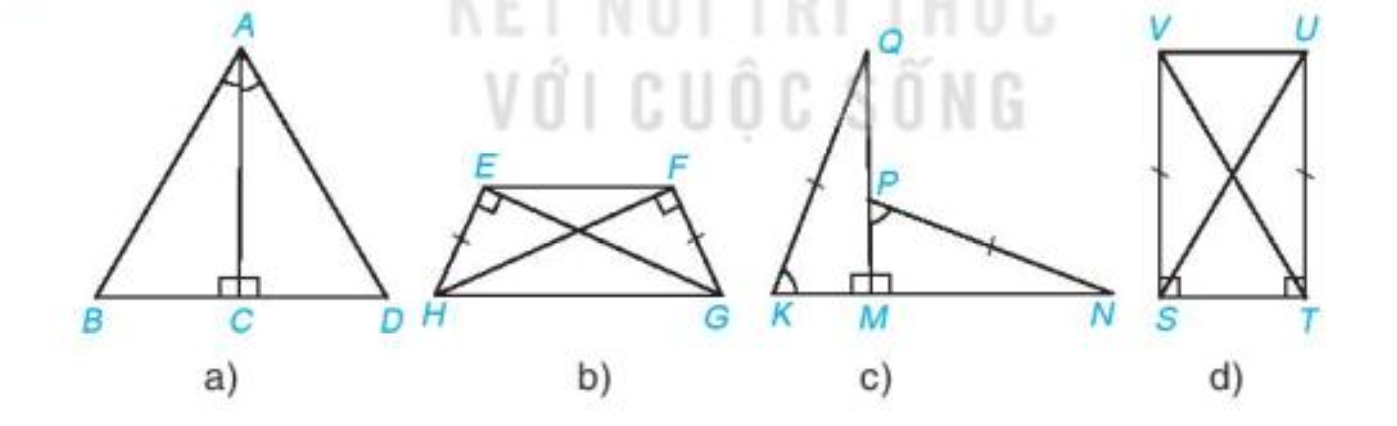
Trong mỗi hình sau có cặp hai tam giác vuông nào bằng nhau? Vì sao?
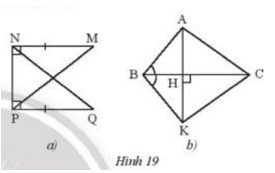
Bài 9 :
Tìm các tam giác vuông bằng nhau trong mỗi hình bên (Hình 19).
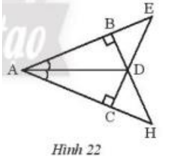
Bài 10 :
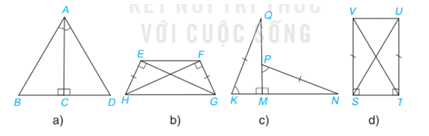
Hãy chỉ ra các cặp tam giác bằng nhau trong Hình 22 và cho biết chúng bằng nhau theo trường hợp nào.
Bài 11 :
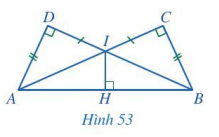
Cho Hình 53 có AD = BC, IC = ID, các góc tại đỉnh C, D, H là góc vuông. Chứng minh:
a) IA = IB;
b) IH là tia phân giác của góc AIB.
Bài 12 :
ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối tia của tia CB lấy điểm N sao cho BM = CN. Kẻ BE ⊥ AM (E ∈ AM), CF ⊥ AN (F ∈ AN).
Qua M kẻ đường thẳng vuông góc với AM, qua N kẻ đường thẳng vuông góc với AN, chúng cắt nhau ở H. Chứng minh ba điểm A, O, H thẳng hàng.
Bài 13 :
Cho tam giác ABC nhọn có AB = AC. Gọi M là trung điểm của đoạn thẳng BC.
a) Chứng minh \(\Delta ABM = \Delta ACM\).
b) Chứng minh \(AM \bot BC\).
c) Trên tia đối của tia MA lấy điểm E sao cho \(MA = ME\). Kẻ \(BH \bot AC\) tại H, \(CK \bot BE\) tại K. Chứng minh \(AC//BE\) và M là trung điểm của đoạn thẳng HK.
Bài 14 :
Cho tam giác ABC có AB = AC. Gọi D là trung điểm của BC. Vẽ CM vuông góc với AB tại M, BN vuông góc với AC tại N. Chứng minh AM = AN.
Bài 15 :
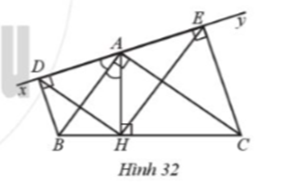
Cho Hình 32 có \(\widehat {BAC} = 90^\circ \), AH vuông góc với BC tại H, \(\widehat {xAB} = \widehat {BAH}\) , Ay là tia đối của tia Ax. BD và CE vuông góc với xy lần lượt tại D và E. Chứng minh:
a) AC là tia phân giác của góc Hay;
b) BD + CE = BC;
c) DH vuông góc với HE.
Bài 16 :
Cho tam giác ABC có AB < AC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA.
a) Chứng minh AC = EB và AC song song với EB.
b) Gọi I là một điểm trên AC, K là một điểm trên EB sao cho AI = EK. Chứng minh ba điểm I, M, K thẳng hàng.
c) Từ E kẻ EH vuông góc với BC tại H. Cho biết \(\widehat {HBE} = 50^\circ ;\widehat {MEB} = 25^\circ \). Tính số đo các góc HEB và HEM.
Bài 17 :
Cho tam giác ABC cân tại đỉnh A. Gọi H là trung điểm của BC.
a) Chứng minh \(AH \bot BC\).
b) Trên tia đối của tia BC lấy điểm M; trên tia đối của tia CB lấy điểm N sao cho \(BM = CN\). Chứng minh rằng \(\Delta ABM = \Delta ACN\).
c) Gọi I là điểm trên AM, K là điểm trên AN sao cho \(BI \bot AM;CK \bot AN\). Chứng minh rằng tam giác AIK cân tại A, từ đó suy ra IK//MN.
Bài 18 :
Cho \(\Delta ABC\) vuông tại \(A\) có \(\angle C = {30^0},\) đường cao \(AH.\) Trên đoạn \(HC\) lấy điểm \(D\) sao cho \(HD = HB.\)a) Chứng minh \(\Delta AHB = \Delta AHD\).
b) Chứng minh \(\Delta ABD\) là tam giác đều.
c) Từ \(C\) kẻ \(CE\) vuông góc với đường thẳng \(AD\)\(\left( {E \in \,AD} \right)\). Chứng minh \(DE = HB\).
d) Từ \(D\) kẻ \(DF\) vuông góc với \(AC\) (\(F\,\)thuộc \(AC\)), \(I\) là giao điểm của \(CE\) và \(AH.\) Chứng minh ba điểm \(I,\,D,\,F\) thẳng hàng.
Bài 19 :
Cho \(\Delta ABC\) vuông tại \(A\), đường trung tuyến \(AM\). Trên tia đối của tia \(MA\) lấy điểm \(D\) sao cho \(DM = MA\).a) Chứng minh \(\Delta AMB = \Delta DMC\).
b) Trên tia đối của tia \(CD\), lấy điểm \(I\) sao cho \(CI = CA\), qua điểm \(I\) vẽ đường thẳng song song với \(AC\) cắt \(AB\) tại \(E\). Chứng minh \(\Delta ACE = \Delta ICE\), từ đó suy ra \(\Delta ACE\) là tam giác vuông cân.
Bài 20 :
Cho tam giác ABC cân tại A.Trên cạnh AB lấy điểm M, trên tia đối của tia CA lấy điểm N sao cho AM + AN = 2AB.a) Chứng minh rằng: BM = CN
b) Chứng minh rằng: BC đi qua trung điểm của đoạn thẳng MN.
c) Đường trung trực của MN và tia phân giác của \(\widehat {BAC}\) cắt nhau tại K. Chứng minh rằng \(\Delta BKM = \Delta CKN\) từ đó suy ra KC vuông góc với AN.
Bài 21 :
Cho \(\Delta ABC\) vuông tại \(A\) có \(\angle C = {30^0},\) đường cao \(AH.\) Trên đoạn \(HC\) lấy điểm \(D\) sao cho \(HD = HB.\)a) Chứng minh \(\Delta AHB = \Delta AHD\).
b) Chứng minh \(\Delta ABD\) là tam giác đều.
c) Từ \(C\) kẻ \(CE\) vuông góc với đường thẳng \(AD\)\(\left( {E \in \,AD} \right)\). Chứng minh \(DE = HB\).
d) Từ \(D\) kẻ \(DF\) vuông góc với \(AC\) (\(F\,\)thuộc \(AC\)), \(I\) là giao điểm của \(CE\) và \(AH.\) Chứng minh ba điểm \(I,\,D,\,F\) thẳng hàng.
Bài 22 :
Cho \(\Delta ABC\) vuông tại \(A\), đường trung tuyến \(AM\). Trên tia đối của tia \(MA\) lấy điểm \(D\) sao cho \(DM = MA\).a) Chứng minh \(\Delta AMB = \Delta DMC\).
b) Trên tia đối của tia \(CD\), lấy điểm \(I\) sao cho \(CI = CA\), qua điểm \(I\) vẽ đường thẳng song song với \(AC\) cắt \(AB\) tại \(E\). Chứng minh \(\Delta ACE = \Delta ICE\), từ đó suy ra \(\Delta ACE\) là tam giác vuông cân.


















Danh sách bình luận