Cho Hình 65 có AM = BN, \(\widehat A = \widehat B\). Chứng minh: OA = OB, OM = ON.

Chứng minh tam giác AOM bằng tam giác BON.
Ta có: \(\widehat A = \widehat B\)
Mà 2 góc này ở vị trí so le trong nên AM // BN
\(\Rightarrow \widehat M = \widehat N\)(2 góc so le trong).
Xét hai tam giác AOM và BON có: \(\widehat A = \widehat B\), AM = BN, \(\widehat M = \widehat N\).
Vậy \(\Delta AOM = \Delta BON\) (g.c.g)
Do đó OA = OB, OM = ON. (2 cạnh tương ứng).

Các bài tập cùng chuyên đề
Bài 1 :
Cho tam giác $ABC$ và tam giác $MNP$ có \(\widehat A = \widehat {M,}\widehat B = \widehat N\) . Cần thêm điều kiện gì để tam giác $ABC$ và tam giác $MNP$ bằng nhau theo trường hợp góc – cạnh – góc:
-
A.
$AC = MP$
-
B.
$AB = MN$
-
C.
$BC = NP$
-
D.
$AC = MN$
Bài 2 :
Cho tam giác \(IKQ\) và tam giác \(MNP\) có \(\widehat I = \widehat {M,}\widehat K = \widehat P\). Cần thêm điều kiện gì để tam giác \(IQK\) và tam giác \(MNP\) bằng nhau theo trường hợp góc – cạnh – góc:
-
A.
\(IQ = MN\)
-
B.
\(IK = MP\)
-
C.
\(QK = NP\)
-
D.
\(IK = MN\)
Bài 3 :
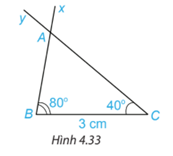
Vẽ đoạn thẳng \(BC = 3\;{\rm{cm}}\). Vẽ hai tia Bx và Cy sao cho \(\widehat {xBC} = {80^\circ },\widehat {yCB} = {40^\circ }\) như Hình 4.33.
Lấy giao điểm \(A\) của hai tia Bx và Cy, ta được tam giác ABC (H.4.33).
Dùng thước thẳng có vạch chia đo độ dài hai cạnh AB, AC của tam giác ABC.
Bài 4 :
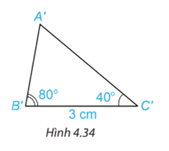
Vẽ thêm tam giác \({A^\prime }{B^\prime }{C^\prime }\) sao cho \({B^\prime }{C^\prime } = 3\;{\rm{cm}}\), \(\widehat {{A^\prime }{B^\prime }{C^\prime }} = {80^\circ },\widehat {{A^\prime }{C^\prime }{B^\prime }} = {40^\circ }.({\rm{H}}.4.34)\).
Dùng thước thẳng có vạch chia hoặc compa so sánh độ dài các cạnh của hai tam giác A B C và \({A^\prime }{B^\prime }{C^\prime }\).
Hai tam giác A B C và \({A^\prime }{B^\prime }{C^\prime }\) có bằng nhau không?
Bài 5 :
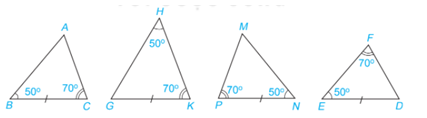
Hai tam giác nào trong Hình 4.35 bằng nhau?
Bài 6 :
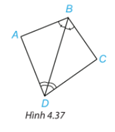
Chứng minh hai tam giác ABD và CBD trong hình 4.37 bằng nhau.
Bài 7 :
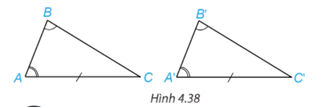
Bạn Lan nói rằng: “Nếu tam giác này có một cạnh cùng một góc kề và góc đối diện tương ứng bằng một cạnh cùng một góc kề và góc đối diện của tam giác kia thì hai tam giác đó bằng nhau” (H.4.38). Theo em bạn Lan nói có đúng không? Vì sao?
Bài 8 :
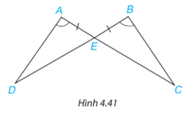
Chứng minh rằng hai tam giác ADE và BCE trong Hình 4.41 bằng nhau.
Bài 9 :
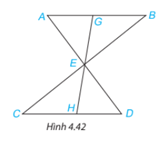
Cho đoạn thẳng AB song song và bằng đoạn thẳng CD như Hình 4.42. Gọi E là giao điểm của hai đường thẳng AD và BC. Hai điểm G và H lần lượt nằm trên AB và CD sao cho G, E, H thẳng hàng. Chứng minh rằng:
a) \(\Delta \)ABE =\(\Delta \)DCE;
b) EG = EH.
Bài 10 :
Cho hai tam giác ABC và DEF thoả mãn \(AB = DE\), \(\widehat {ABC} = \widehat {DEF} = {70^\circ }\), \(\widehat {BAC} = \widehat {EDF} = {60^\circ }\), \(AC = 6\;{\rm{cm}}.\)
Tính độ dài cạnh DF.
Bài 11 :
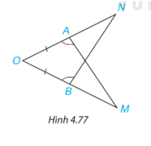
Trong Hình 4.77, có AO = BO,\(\widehat {OAM} = \widehat {OBN}\). Chứng minh rằng AM = BN.
Bài 12 :
Cho 2 tam giác ABC và MNP bất kì, thoả mãn \(\widehat {ABC} = \widehat {PNM},\widehat {ACB} = \widehat {NPM}\) và BC = PN. Những câu nào dưới đây đúng?
a) \(\Delta ABC = \Delta PNM\)
b) \(\Delta ABC = \Delta NPM\)
c) \(\Delta ABC = \Delta MPN\)
d) \(\Delta ABC = \Delta MNP\)
Bài 13 :
Cho các điểm A, B, C, D như Hình 4.25, biết rằng \(\widehat {BAC} = \widehat {BAD}\) và \(\widehat {BCA} = \widehat {BDA}\). Chứng minh rằng \(\Delta ABC = \Delta ABD\).
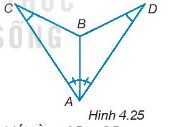
Bài 14 :
Hai tam giác ABC và MNP bằng nhau khi và chỉ khi điều nào dưới đây xảy ra?
A. BC = NP, \(\widehat B = \widehat P,\widehat C = \widehat N\)
B. BC = NP, \(\widehat B = \widehat N,\widehat A = \widehat P\)
C. BC = NP, \(\widehat B = \widehat N,\widehat C = \widehat P\)
D. BC = NP, \(\widehat A = \widehat M,\widehat C = \widehat N\)
Bài 15 :
Chứng minh rằng hai tam giác ADE và BCE trong hình dưới đây bằng nhau.
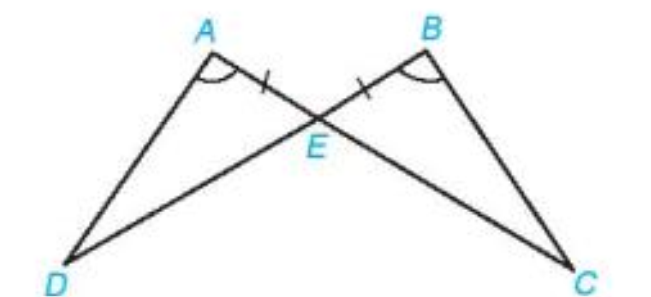
Bài 16 :
Cho đoạn thẳng AB song song và bằng đoạn thẳng CD như hình dưới đây. Gọi E là giao điểm của hai đường thẳng AD và BC. Hai điểm G và H lần lượt nằm trên AB và CD sao cho G,H,E thẳng hàng Chứng minh rằng
a) \(\Delta ABE = \Delta DCE\)
b) EG = EH.
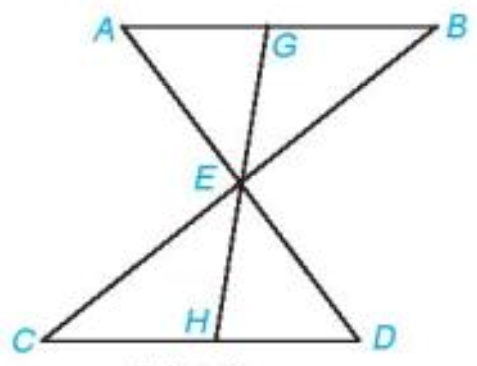
Bài 17 :
Cho hình vẽ dưới đây, biết rằng AC = BD, BC = AD, \(\widehat {CAD} = {90^o},\widehat {DAB} = {30^o}\). Chứng minh rằng \(\Delta ABC = \Delta BAD\)
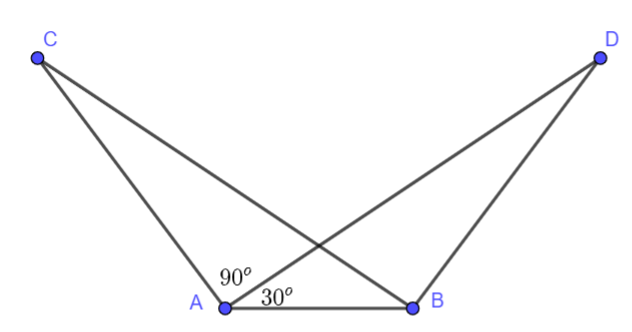
Bài 18 :
Cho hai tam giác ABC và DEF thỏa mãn AB = DE, \(\widehat E = \widehat B = {70^o},\widehat A = \widehat D = {60^o}\), AC = 6cm. Hãy tính DF.
Bài 19 :
Cho tia Oz là phân giác của góc xOy. Lấy các điểm A, B, C lần lượt thuộc các tia Ox, Oy, Oz sao cho \(\widehat {CAO} = \widehat {CBO}\)
a) Chứng minh rằng \(\Delta OAC = \Delta OBC\)
b) Lấy điểm M trên tia đối của tia CO. Chứng minh rằng \(\Delta MAC = \Delta MBC\)
Bài 20 :
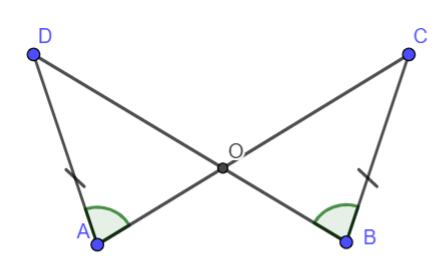
Cho hình vẽ dưới đây. Biết rằng AD = BC, \(\widehat {DAC} = \widehat {CBD}\), O là giao điểm của AC và BD. Chứng minh rằng AO = BO.
Bài 21 :
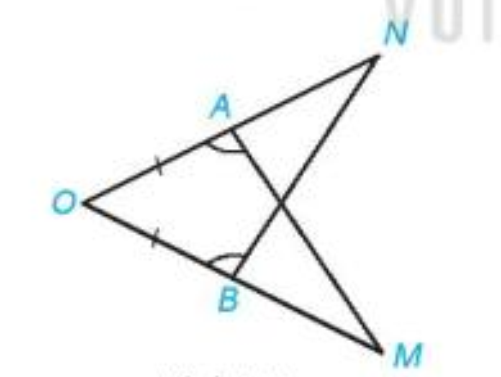
Trong hình vẽ sau ta có AO = BO, \(\widehat {OAM} = \widehat {OBN}\). Chứng minh rằng AM = BN.
Bài 22 :
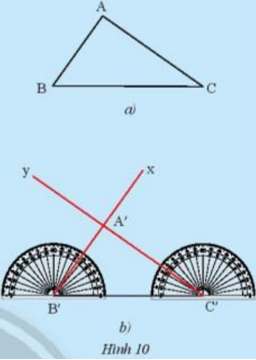
Cho tam giác ABC như trong Hình 10a. Lấy một tờ giấy, trên đó vẽ tam giác A’B’C’có B’C’ = BC, \(\widehat {B'} = \widehat B\), \(\widehat {C'} = \widehat C\)theo các bước:
-Vẽ đoạn thẳng B’C’ = BC.
-Ở về cùng một phía của tờ giấy đối với đường thẳng B’C’vẽ \(\widehat {C'B'x} = \widehat {CBA}\), và vẽ \(\widehat {B'C'y} = \widehat {BCA}\).
-Vẽ giao điểm A’của hai tia B’x và C’y, ta được tam giác A’B’C’ (Hình 10b).
Em hãy cắt rời tam giác A’B’C’ra khỏi tờ giấy vừa vẽ và thử xem có thể đặt chồng khít tam giác A’B’C’lên tam giác ABC hay không.
Theo em, hai tam giác ABC và A’B’C’ trong trường hợp này có bằng nhau hay không?
Bài 23 :
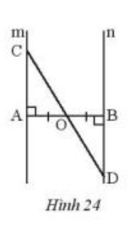
Cho đoạn thẳng AB có O là trung điểm. Vẽ hai đường thẳng m và n lần lượt vuông góc với AB tại A và B. Lấy điểm C trên m, CO cắt n tại D (Hình 24). Chứng minh rằng O là trung điểm CD.
Bài 24 :
Có hai trạm quan sát A, B và một trạm quan sát C ở giữa hồ. Do không thể đo trực tiếp được khoảng cách từ A và từ B đến C nên người ta làm như sau (Hình 55):
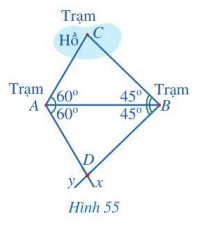
- Đo góc BAC được 60°, đo góc ABC được 45°;
- Kẻ tia Ax sao cho \(\widehat {BAx} = 60^\circ \), kẻ tia By sao cho \(\widehat {ABy} = 45^\circ \), xác định giao điểm D của hai tia đó;
- Đo khoảng cách AD và BD.
Tại sao lại có AC = AD và BC = BD?
Bài 25 :
Cho hai tam giác ABC và A’B’C’ thỏa mãn: BC = B’C’ = 3 cm, \(\widehat B = \widehat {B'} = 60^\circ ,\widehat C = 50^\circ ,\widehat {A'} = 70^\circ \). Hai tam giác ABC và A’B’C’ có bằng nhau không? Vì sao?
Bài 26 :
Giải thích bài toán ở phần mở đầu.
Có hai trạm quan sát A, B và một trạm quan sát C ở giữa hồ. Do không thể đo trực tiếp được khoảng cách từ A và từ B đến C nên người ta làm như sau (Hình 55):

- Đo góc BAC được 60°, đo góc ABC được 45°;
- Kẻ tia Ax sao cho \(\widehat {BAx} = 60^\circ \), kẻ tia By sao cho \(\widehat {ABy} = 45^\circ \), xác định giao điểm D của hai tia đó;
- Đo khoảng cách AD và BD.
Tại sao lại có AC = AD và BC = BD?
Bài 27 :
Cho hai tam giác ABC và A’B’C’ thỏa mãn: AB = A’B’, \(\widehat A = \widehat {A'},\widehat C = \widehat {C'}\). Hai tam giác ABC và A’B’C’ có bằng nhau không? Vì sao?
Bài 28 :
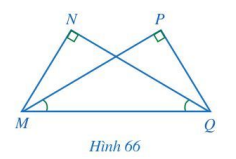
Cho Hình 66 có \(\widehat N = \widehat P = 90^\circ ,\widehat {PMQ} = \widehat {NQM}\). Chứng minh MN = QP, MP = QN.
Bài 29 :
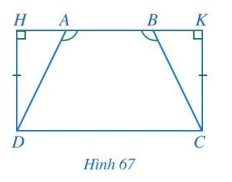
Cho Hình 67 có \(\widehat {AHD} = \widehat {BKC} = 90^\circ ,DH = CK,\widehat {DAB} = \widehat {CBA}\). Chứng minh AD = BC.
Bài 30 :
Cho tam giác ABC có \(\widehat B > \widehat C\). Tia phân giác góc BAC cắt cạnh BC tại điểm D.
a) Chứng minh \(\widehat {ADB} < \widehat {ADC}\).
b) Kẻ tia Dx nằm trong góc ADC sao cho \(\widehat {ADx} = \widehat {ADB}\). Giả sử tia Dx cắt cạnh AC tại điểm E. Chứng minh: \(\Delta ABD = \Delta AED,AB < AC\).


















Danh sách bình luận