Thực hiện phép tính:
a) \({x^2}.{x^4}\);
b) \(3{x^2}.{x^3}\);
c) \(a{x^m}.b{x^n}\) (a ≠ 0; b ≠ 0; m, n \(\in\) N).
Muốn thực hiện được phép tính, ta nhân hệ số của đơn thức thứ nhất với đơn thức thứ 2. Và nhân lũy thừa của biến trong đơn thức thứ nhất với lũy thừa của biến trong đơn thức thứ 2.
\({x^m}.{x^n} = {x^{m + n}}\)
a) \({x^2}.{x^4} = {x^{2 + 4}} = {x^6}\).
b) \(3{x^2}.{x^3} = 3.1.{x^{2 + 3}} = 3{x^5}\).
c) \(a{x^m}.b{x^n} = a.b.{x^{m + n}}\) (a ≠ 0; b ≠ 0; m, n \(\in\) N).

Các bài tập cùng chuyên đề
Bài 1 :
Hãy nhắc lại cách nhân hai đơn thức và tính (12x3).(-5x2)
Bài 2 :
Tính:
a) \(3{x^5}.5{x^8}\);
b) \( - 2{x^{m + 2}}.4{x^{n - 2}}\) (m, n \(\in\) N; n > 2).
Bài 3 :
Bể cá cảnh nhà bạn Khôi có dạng hình lập phương với độ dài cạnh x (dm). Ban đầu mực nước ở bể cao x − 1 (dm), bạn Khôi đặt một khối đá dạng núi cảnh chìm vào nước trong bể thì mực nước ở bể cao thêm 0,5 dm.
a) Tính thể tích nước có ở bể lúc đầu theo x
b) Tính thể tích khối đá mà bạn Khôi thả chìm vào nước trong bể theo x
c) Tính thể tích nước và khối đá mà bạn Khôi thả chìm vào nước trong bể theo x
Bài 4 :
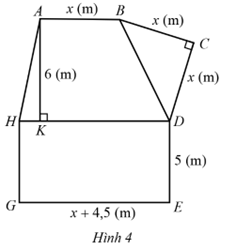
Bác Na có mảnh đất được mô tả như Hình 4. Bác chia mảnh đất đó thành các khu vực: khu trồng rau là hình thang ABDH (AB // DH, \(AK \bot HD\)), khu trồng cây ăn quả là tam giác BCD và khu chăn nuôi là hình chữ nhật HDEG. Tính diện tích của mảnh đất đó theo các kích thước AB = x (m), BC = x (m), CD = x (m),
DE = 5 (m), \(EG = x + 4,5\) (m), \(AK = 6\) (m)
Bài 5 :
Tháng 5 năm 2019, nhiều đại biểu trên cả nước đã “hội quân” trên một tàu kiểm ngư rời cảng biển quốc tế Cam Ranh để bắt đầu hải trình nối tình yêu đất liền với biển đảo Trường Sa. Do thời tiết xấu, tàu kiểm ngư đã giảm 15% tốc độ so với tốc độ đã định. Giả sử tốc độ đã định của tàu kiểm ngư là x hải lí/giờ. Viết biểu thức biểu thị số hải lí mà tàu kiểm ngư đã đi với số thời gian:
a) 1 giờ
b) 4 giờ
c) y giờ
Bài 6 :
Tính:
a) \(\left( { - 0,5x} \right).\left( {3{x^2}} \right).\left( { - 4{x^3}} \right)\);
b) \(4,7{x^4} - \sqrt 9 {x^4} + 0,3{x^4}\).
Bài 7 :
Một bể chứa nước có dạng hình hộp chữ nhật được thiết kế với kích thước theo tỉ lệ:
Chiều cao: chiều rộng: chiều dài\( = 1:2:3\).
Trong bể hiện còn \(0,7{m^3}\) nước. Gọi chiều cao của bể là x (mét).
Hãy viết đa thức biểu thị số mét khối nước cần phải bơm thêm vào bể để bể đầy nước. Xác định bậc của đa thức đó.
Bài 8 :
Tích của hai đơn thức là một đơn thức (nếu tất cả các hệ số đều khác 0):
A. Có hệ số bằng tổng các hệ số và có bậc bằng tổng các bậc của hai đơn thức đã cho.
B. Có hệ số bằng tổng các hệ số và có bậc bằng tích các bậc của hai đơn thức đã cho.
C. Có hệ số bằng tích các hệ số và có bậc bằng tổng các bậc của hai đơn thức đã cho.
D. Có hệ số bằng tích các hệ số và có bậc bằng tích các bậc của hai đơn thức đã cho.


















Danh sách bình luận