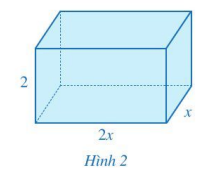
Một số tình huống trong cuộc sống dẫn đến việc cộng, trừ hai đa thức một biến, chẳng hạn, ta phải tính tổng diện tích các mặt của hình hộp chữ nhật (Hình 2) có độ dài hai cạnh đáy là x (m), 2x (m) và chiều cao là 2 (m).
Phép cộng, phép trừ hai đa thức một biến được thực hiện như thế nào?
Đọc lại bài (Phần I để xem cách cộng hai đa thức và phần II để xem cách trừ hai đa thức).
a) Cộng hai đa thức:
Để cộng hai đa thức một biến (theo cột dọc), ta có thể làm như sau:
- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
- Đặt hai đơn thức có cùng số mũ của biến ở cùng cột;
- Cộng hai đơn thức trong từng cột, ta có tổng cần tìm.
Để cộng hai đa thức một biến (theo hàng ngang), ta có thể làm như sau:
- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
- Viết tổng hai đơn thức theo hàng ngang;
- Nhóm các đơn thức có cùng số mũ của biến với nhau;
- Thực hiện phép tính trong từng nhóm, ta được tổng cần tìm.
b) Trừ hai đa thức:
Để trừ đa thức P(x) cho đa thức Q(x) (theo cột dọc), ta có thể làm như sau:
- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
- Đặt hai đơn thức có cùng số mũ của biến ở cùng cột sao cho đơn thức P(x) ở trên và đơn thức của Q(x) ở dưới;
- Trừ hai đơn thức trong từng cột, ta có hiệu cần tìm.
Để trừ đa thức P(x) cho đa thức Q(x) (theo hàng ngang), ta có thể làm như sau:
- Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;
- Viết hiệu P(x) – Q(x) theo hàng ngang, trong đó đa thức Q(x) được đặt trong dấu ngoặc;
- Sau khi bỏ dấu ngoặc và đổi dấu mỗi đơn thức trong dạng thu gọn của đa thức Q(x), nhóm các đơn thức có cùng số mũ của biến với nhau;
- Thực hiện phép tính trong từng nhóm, ta được hiệu cần tìm.

Các bài tập cùng chuyên đề
Bài 1 :
Cho 3 đa thức:
A( x) = 6x2 – 3x + x3 – 4x2 – 5
B(x) = -2x2 – 3x + 7 +2x2 + x3
\(C(x) = 6{x^2} - 3x + 4 - 2{x^3} - 2x\)
Bài 2 :
Cho hai đa thức \(A\left( x \right) = 5{x^4} - 7{x^2} - 3x - 6{x^2} + 11x - 30\) và \(B\left( x \right) = - 11{x^3} + 5x - 10 + 13{x^4} - 2 + 20{x^3} - 34x\)
a) Thu gọn hai đa thức \(A\left( x \right)\) và \(B\left( x \right)\) và sắp xếp theo lũy thừa giảm dần của biến.
b) Tính \(A\left( x \right) - B\left( x \right)\).
Bài 3 :
Cho đa thức A = x4 – 3x2 – 2x + 1. Tìm các đa thức B và C sao cho:
A + B = 2x5 + 5x3 – 2
A – C = x3
Bài 4 :
Cho hai đa thức:
\(A = 6{x^4} - 4{x^3} + x - \dfrac{1}{3};B = - 3{x^4} - 2{x^3} - 5{x^2} + x + \dfrac{2}{3}\)
Tính A + B và A - B
Bài 5 :
Cho các đa thức:
\(A = 3{x^4} - 2{x^3} - x + 1;B = - 2{x^3} + 4{x^2} + 5x;C = - 3{x^4} + 2{x^2} + 5\)
Tính A + B + C; A – B + C và A – B – C
Bài 6 :
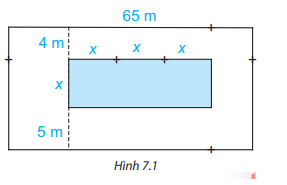
Trên một mảnh đất hình chữ nhật có chiều dài 65 m, người ta định làm một bể bơi có chiều rộng là x mét, chiều dài gấp 3 lần chiều rộng. Sơ đồ và kích thước cụ thể (tính bằng mét) đươc cho trong Hình 7.1. Tìm đa thức ( biến x):
a) Biểu thị diện tích bể bơi
b) Biểu thị diện tích mảnh đất
c) Biểu thị diện tích phần đất xung quanh bể bơi.
Bài 7 :
Cho hai đa thức P = -5x4 +3x3 + 7x2 + x – 3 và Q = 5x4 – 4x3 – x2 + 3x + 3
a) Xác định bậc của mỗi đa thức P + Q và P – Q.
b) Tính giá trị của mỗi đa thức P + Q và P – Q tại x = 1; x = - 1
c) Đa thức nào trong hai đa thức P + Q và P – Q có nghiệm là x = 0?
Bài 8 :
Cho hai đa thức P(x) = \( - 3{x^4} - 8{x^2} + 2x\) và Q(x) = \(5{x^3} - 3{x^2} + 4x - 6\).
Hãy tính P(x) + Q(x) và P(x) – Q(x).
Bài 9 :
Cho đa thức M(x) = \(7{x^3} - 2{x^2} + 8x + 4\)
Tìm đa thức N(x) sao cho M(x) + N(x) = \(3{x^2} - 2x\)
Bài 10 :
Cho ba đa thức P(x) = \(9{x^4} - 3{x^3} + 5x - 1\)
Q(x) = \( - 2{x^3} - 5{x^2} + 3x - 8\)và R(x) = \( - 2{x^4} + 4{x^2} + 2x - 10\)
Tính P(x) + Q(x) + R(x) và P(x) – Q(x) – R(x)
Bài 11 :
a) Thực hiện phép tính: \((3x - 1) + \left[ {(2{x^2} + 5x) + (4 - 3x)} \right]\)
b) Cho A = 4x + 2, C = \(5 - 3{x^2}\). Tìm đa thức B sao cho A + B = C
Bài 12 :
Cho đa thức \(M(x) = 2{x^4} - 5{x^3} + 7{x^2} + 3x\).
Tìm các đa thức N(x), Q(x) sao cho:
\(N(x) - M(x) = - 4{x^4} - 2{x^3} + 6{x^2} + 7\)
và \(M(x) + Q(x) = 6{x^5} - {x^4} + 3{x^2} - 2\)
Bài 13 :
Cho hai đa thức: \(R(x) = - 8{x^4} + 6{x^3} + 2{x^2} - 5x + 1\) và \(S(x) = {x^4} - 8{x^3} + 2x + 3\). Tính:
a) R(x) + S(x);
b) R(x) – S(x).
Bài 14 :
Xác định bậc của hai đa thức là tổng, hiệu của:
\(A(x) = - 8{x^5} + 6{x^4} + 2{x^2} - 5x + 1\) và \(B(x) = 8{x^5} + 8{x^3} + 2x - 3\).
Bài 15 :
Bạn Minh cho rằng “Tổng của hai đa thức bậc bốn luôn luôn là đa thức bậc bốn”. Bạn Quân cho rằng “Hiệu của hai đa thức bậc bốn luôn luôn là đa thức bậc bốn”. Hai bạn Minh và Quân nói như vậy có đúng không? Giải thích vì sao.
Bài 16 :
Cho hai đa thức:
\(A(x) = 4{x^4} + 6{x^2} - 7{x^3} - 5x - 6\) và \(B(x) = - 5{x^2} + 7{x^3} + 5x + 4 - 4{x^4}\).
a) Tìm đa thức M(x) sao cho \(M(x) = A(x) + B(x)\).
b) Tìm đa thức C(x) sao cho \(A(x) = B(x) + C(x)\).
Bài 17 :
Cho biết \(A\left( x \right) - \left( {9{x^3} + 8{x^2} - 2x - 7} \right) = - 9{x^3} - 8{x^2} + 5x + 11\)
Tìm đa thức \(A\left( x \right)\)
Bài 18 :
Cho hai đa thức \(P\left( x \right) = 6{x^5} + 15 - 7x - 4{x^2} - {x^5}\); \(Q\left( x \right) = - 5{x^5} - 2x + 4{x^2} + 5x - 7\).
Tìm bậc và hệ số tự do của đa thức \(K(x)\) biết \(K(x) = P(x) - Q(x)\).
Bài 19 :
Cho hai đa thức \(P\left( x \right) = 6{x^5} + 15 - 7x - 4{x^2} - {x^5}\); \(Q\left( x \right) = - 5{x^5} - 2x + 4{x^2} + 5x - 7\).
Bài 20 :
Cho hai đa thức \(A\left( x \right) = {x^4} - 5{x^3} + {x^2} + 5x - \dfrac{1}{3};B\left( x \right) = {x^4} - 2{x^3} + {x^2} - 5x - \dfrac{2}{3}.\)
Hãy tính \(A\left( x \right) + B\left( x \right);A\left( x \right) - B\left( x \right)\)
Bài 21 :
Cho đa thức \(H\left( x \right) = {x^4} - 3{x^3} - x + 1\). Tìm đa thức P(x) và Q(x) sao cho
a)\(H\left( x \right) + P\left( x \right) = {x^5} - 2{x^2} + 2\)
b)\(H\left( x \right) - Q\left( x \right) = - 2{x^3}\)
Bài 22 :
Em hãy viết hai đa thức tuỳ ý A(x) và B(x). Sau đó tính \(C\left( x \right) = A\left( x \right) - B\left( x \right)\) và \(C'\left( x \right) = B\left( x \right) - A\left( x \right)\), rồi so sánh và nêu nhận xét về bậc, các hệ số của C(x) và C’(x).
Bài 23 :
Cho các đa thức \(A\left( x \right) = 2{x^3} - 2{x^2} + x - 4;B\left( x \right) = 3{x^3} - 2x + 3;C\left( x \right) = - {x^3} + 1\). Hãy tính:
a) \(A\left( x \right) + B\left( x \right) + C\left( x \right);\)
b) \(A\left( x \right) - B\left( x \right) - C\left( x \right).\)
Bài 24 :
Cho hai đa thức \(P\left( x \right) = - 4{x^4} - 3{x^2} + 7\) và \(Q\left( x \right) = 2{x^4} - 5{x^2} + 8x - 1\). Hãy tính \(P\left( x \right) + Q\left( x \right)\) và \(P\left( x \right) - Q\left( x \right)\).
Bài 25 :
Cho đa thức \(M\left( x \right) = 4{x^3} - 7{x^2} + 2x - 9\). Tìm đa thức \(N\left( x \right)\) sao cho \(M\left( x \right) + N\left( x \right) = 2{x^3} - 6x\).
Bài 26 :
Cho tam giác (xem Hình 2) có chu vi bằng \(12t - 6\), Hãy tìm cạnh chưa biết của tam giác đó
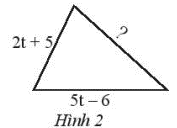
Bài 27 :
Cho đa thức \(M\left( x \right) = 3{x^5} - 4{x^3} + 9x + 2\). Tìm các đa thức \(N\left( x \right)\), \(Q\left( x \right)\) sao cho \(N\left( x \right) - M\left( x \right) = - 5{x^4} - 4{x^3} + 2{x^2} + 8x\) và \(Q\left( x \right) + M\left( x \right) = 3{x^4} - 2{x^3} + 9{x^2} - 7\)
Bài 28 :
Tìm các đa thức P(x) và Q(x), biết P(x) + Q(x) = x2 + 1 và P(x) - Q(x) = 2x.
Bài 29 :
a) Cho các đa thức: \(A(x) = {x^2} - 0,45x + 1,2;B(x) = 0,8{x^2} - 1,2x;C(x) = 1,6{x^2} - 2x\)
Tính \(A(x) + B(x) - C(x)\)
b) Cho các đa thức: \(M(y) = {y^2} - 1,75y - 3,2;N(y) = 0,3{y^2} + 4;P(y) = 2y - 7,2\)
Tính \(M(y) - N(y) - P(y)\)
Bài 30 :
Cho hai đa thức: \(F(x) = 2{x^4} - {x^3} + x - 3;G(x) = - {x^3} + 5{x^2} + 4x + 2\)
a) Tìm đa thức H(x) sao cho \(F(x) + H(x) = 0\)
b) Tìm đa thức K(x) sao cho \(K(x) - G(x) = F(x)\)


















Danh sách bình luận