Đề bài

Cho tam giác đều $ABC$ cạnh $a$, $I$ là trung điểm của $BC$, $D$ là điểm đối xứng với $A$ qua $I$. Vẽ đoạn thẳng $S{\rm{D}}$ có độ dài bằng $\frac{{a\sqrt 6 }}{2}$ và vuông góc với $\left( {ABC} \right)$. Chứng minh rằng:

a) $\left( {SBC} \right) \bot \left( {SAD} \right)$;

b) $\left( {SAB} \right) \bot \left( {SAC} \right)$.

Phương pháp giải

Cách chứng minh hai mặt phẳng vuông góc: chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng.

Lời giải của GV Loigiaihay.com

 

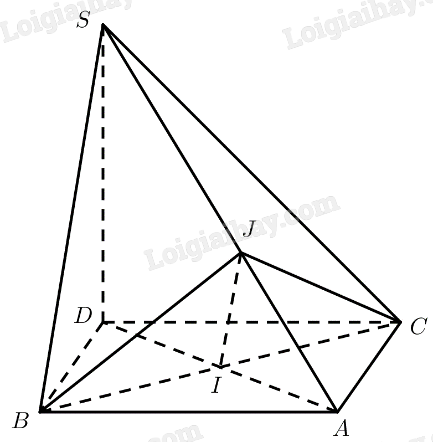
a) $ABDC$ là hình thoi $\Rightarrow A{\rm{D}} \bot BC$

$S{\rm{D}} \bot \left( {ABC} \right) \Rightarrow S{\rm{D}} \bot BC$

$\left. \begin{array}{l} \Rightarrow BC \bot \left( {SA{\rm{D}}} \right)\\BC \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow \left( {SBC} \right) \bot \left( {SA{\rm{D}}} \right)$

b) Kẻ $IJ \bot SA\left( {J \in SA} \right)$.

$\Delta ABC$ đều $\Rightarrow AI = \frac{{a\sqrt 3 }}{2} \Rightarrow A{\rm{D}} = 2AI = a\sqrt 3$

$\Delta SAD$ vuông tại $D$ $\Rightarrow S{\rm{A}} = \sqrt {S{D^2} + A{{\rm{D}}^2}}  = \frac{{3a\sqrt 2 }}{2}$

Xét $\Delta SAD$ và $\Delta IAJ$có:

$\begin{array}{l}\widehat {SDA} = \widehat {IJA} = {90^0}\\\widehat A\,\,chung\end{array}$

Suy ra $\Delta SAD\,\infty \,\Delta IAJ\,(g.g) \Rightarrow \frac{{JI}}{{SD}} = \frac{{AI}}{{SA}} \Rightarrow JI = \frac{{SD.AI}}{{SA}} = \frac{{\frac{{a\sqrt 6 }}{2}.\frac{{a\sqrt 3 }}{2}}}{{\frac{{3a\sqrt 2 }}{2}}} = \frac{a}{2}$

Nên $JI = \frac{{BC}}{2}$

Tam giác $BCJ$ có $IJ$ là trung tuyến và $IJ = \frac{1}{2}BC$

Vậy tam giác $BCJ$ vuông tại $J \Rightarrow BJ \bot JC$

$\begin{array}{l}\left. \begin{array}{l}BC \bot \left( {SA{\rm{D}}} \right) \Rightarrow BC \bot SA\\IJ \bot SA\end{array} \right\} \Rightarrow SA \bot \left( {BCJ} \right)\\\left. \begin{array}{l} \Rightarrow SA \bot BJ\\BJ \bot JC\end{array} \right\} \Rightarrow BJ \bot \left( {SAC} \right)\end{array}$

Mà $BJ \subset \left( {SAB} \right)$

Vậy $\left( {SAB} \right) \bot \left( {SAC} \right)$.