Điền vào chỗ trống sau: \({\left( {x + 2} \right)^2} = {x^2} + ... + 4\)
-
A.
\(2x\).
-
B.
\(4x\).
-
C.
\(2\).
-
D.
\(4\).
Dựa vào hằng đẳng thức bình phương của một tổng.
Ta có: \({\left( {x + 2} \right)^2} = {x^2} + 4x + 4\).
Chỗ trống cần điền là \(4x\).
Đáp án B.
Đáp án : B
Các bài tập cùng chuyên đề
Với hai số a,b bất kì, thực hiện phép tính \(\left( {a + b} \right).\left( {a + b} \right)\).
Từ đó rút ra liên hệ giữa \({\left( {a + b} \right)^2}\) và \({a^2} + 2ab + {b^2}\)
- Khai triển \({\left( {2b + 1} \right)^2}\)
- Viết biểu thức \(9{y^2} + 6yx + {x^2}\) dưới dạng bình phương của một tổng.
Tính nhanh giá trị của biểu thức:
\({x^2} + \dfrac{1}{2}x + \dfrac{1}{{16}}\) tại x=99,75.
Chứng minh đẳng thức \({\left( {10a + 5} \right)^2} = 100a\left( {a + 1} \right) + 25\). Từ đó em hãy nêu một quy tắc tính nhẩm bình phương của một số có tận cùng là 5.
Áp dụng: Tính \({25^2};{35^2}\).
Biểu thức \(25{x^2} + 20xy + 4{y^2}\) viết dưới dạng bình phương của một tổng là:
A. \({\left[ {5x + \left( { - 2y} \right)} \right]^2}\)
B. \({\left[ {2x + \left( { - 5y} \right)} \right]^2}\)
C. \({\left( {2x + 5y} \right)^2}\)
D. \({\left( {5x + 2y} \right)^2}\).
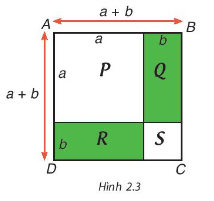
Sử dụng Hình 2.3, bằng cách tính diện tích hình vuông ABCD theo hai cách, hãy giải thích hằng đẳng thức \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\).
Tính:
a) \({\left( {3x + 1} \right)^2}\)
b) \({\left( {4x + 5y} \right)^2}\)
c) \({\left( {5x - \dfrac{1}{2}} \right)^2}\)
d) \({\left( { - x + 2{y^2}} \right)^2}\)
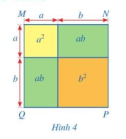
Diện tích của hình vuông MNPQ (hình 4) có thể được tính theo những cách nào?
Cho \(a\) và \(b\) là hai số thực bất kì.
1. Thực hiện phép tính \(\left( {a + b} \right)\left( {a + b} \right)\)
2. Hãy cho biết: \({\left( {a + b} \right)^2} = ?\)
Tính:
a) \({\left( {a + 4} \right)^2}\);
b) \({\left( {2u + 5v} \right)^2}\)
Viết các biểu thức sau dưới dạng bình phương của một tổng:
a) \(16{a^2} + 8a + 1\);
b) \({x^2} + 25{y^2} + 10xy\)
Tính nhanh: \( (0,76)^3 + (0,24)^3+3.0,76.0,24 \)
Biểu thức \({\left( {x - 2y} \right)^2}\) bằng:
A. \({x^2} + 2xy + 2{y^2}\)
B. \({x^2} - 2xy + 2{y^2}\)
C. \({x^2} + 4xy + 4{y^2}\)
D. \({x^2} - 4xy + 4{y^2}\)
a) Biết số tự nhiên a chia 3 dư 2. Chứng minh \({a^2}\) chia 3 dư 1.
b) Biết số tự nhiên a chia 5 dư 3. Chứng minh \({a^2}\) chia 5 dư 4.
Chứng minh rằng với mọi số tự nhiên n, ta có:
\({\left( {n + 2} \right)^2}\;-{n^2}\) chia hết cho 4.
Biết số tự nhiên a chia 3 dư 2. Chứng minh rằng \({a^2}\) chia 3 dư 1.
Biểu thức \({x^2} + x + \frac{1}{4}\) viết được dưới dạng bình phương của một tổng là
A.\({\left[ {x + \left( { - \frac{1}{2}} \right)} \right]^2}\).
B.\({\left( {x + \frac{1}{2}} \right)^2}\).
C.\({\left( {2x + \frac{1}{2}} \right)^2}\)
D.\({\left( {\frac{1}{2}x + 1} \right)^2}\)
Tính nhanh giá trị của biểu thức
\({x^2} + \frac{1}{2}x + \frac{1}{{16}}\) tại \(x = 99,75\).
Chứng minh đẳng thức \({\left( {10a + 5} \right)^2}\; = 100a\left( {a + 1} \right) + 25\). Từ đó, em hãy nêu một quy tắc tính nhẩm bình phương của một số có tận cùng là 5.
Áp dụng: Tính \({25^2},{35^2}\).
Biểu thức \(25{x^2}\; + 20xy + 4{y^2}\) viết dưới dạng bình phương của một tổng là:
A. \({\left[ {5x\; + \;\left( { - 2y} \right)} \right]^2}\).
B. \({\left[ {2x\; + \;\left( { - 5y} \right)} \right]^2}\).
C. \({\left( {2x + 5y} \right)^2}\).
D. \({\left( {5x + 2y} \right)^2}\).
Sử dụng Hình 2.3, bằng cách tính diện tích hình vuông ABCD theo hai cách, hãy giải thích hằng đẳng thức \({\left( {a + b} \right)^2}\; = {a^2}\; + 2ab + {b^2}\).
Khai triển \((3x+2)^2\) ta được
Cho \({a^2} + {b^2} + {c^2} = ab + bc + ca\;\) và \(a + b + c = 2022\). Tính \(a, b, c\).
Chọn câu đúng:
Khai triển \({\left( {3x + 4y} \right)^2}\), ta được:
