Tìm hệ số trong đơn thức \(\frac{1}{3}a{b^2}xy\) với a, b là hằng số
-
A.
\(\frac{1}{3}\).
-
B.
\(\frac{1}{3}{a^2}b\).
-
C.
\(\frac{1}{3}a{b^2}\).
-
D.
\(xy\).
Trong một đơn thức thu gọn, phần số còn gọi là hệ số, phần còn lại gọi là phần biến.
Vì a, b là hằng số nên hệ số trong đơn thức là \(\frac{1}{3}a{b^2}\).
Đáp án C.
Đáp án : C
Các bài tập cùng chuyên đề
Biểu thức \({x^2} - 2x\) có phải là đơn thức một biến không? Vì sao? Hãy cho một vài ví dụ về đơn thức một biến.
Xét các biểu thức đại số:
\( - 5{x^2}y;{x^3} - \dfrac{1}{2}x;17{z^4}; - \dfrac{1}{5}{y^2}5; - 2x + 7y;xy4{x^2};x + 2y - z.\)
Hãy sắp xếp các biểu thức đó thành hai nhóm:
Nhóm 1: Những biểu thức có chứa phép cộng hoặc phép trừ.
Nhóm 2: Các biểu thức còn lại.
Nếu hiểu đơn thức (nhiều biến) tương tự đơn thức một biến thì theo em, nhóm nào trong hai nhóm trên bao gồm những đơn thức?
Trong các biểu thức sau đây, biểu thức nào là đơn thức?
\(3{x^3}y; - 4;\left( {3 - x} \right){x^2}{y^2};12{x^5}; - \dfrac{5}{9}xyz;\dfrac{{{x^2}y}}{2};\dfrac{3}{x} + {y^2}.\)
Còn em nghĩ sao?
Cho biết hệ số, phần biến và bậc của mỗi đơn thức sau:
\(2,5x; - \dfrac{1}{4}{y^2}{z^3};0,35x{y^2}{z^4}.\)
Thu gọn và xác định bậc của đơn thức \(4,5{x^2}y\left( { - 2} \right)xyz.\)
Trong các biểu thức sau, biểu thức nào là đơn thức?
\( - x;\left( {1 + x} \right){y^2};\left( {3 + \sqrt 3 } \right)xy;0;\dfrac{1}{y}{x^2};2\sqrt {xy} .\)
Cho các đơn thức:
\(A = 4x\left( { - 2} \right){x^2}y;B = 12,75xyz;C = \left( {1 + 2.4,5} \right){x^2}y.\dfrac{1}{5}{y^3};D = \left( {2 - \sqrt 5 } \right)x.\)
a) Liệt kê các đơn thức thu gọn trong các đơn thức đã cho và thu gọn các đơn thức còn lại.
b) Với mỗi đơn thức nhận được, hãy cho biết hệ số, phần biến và bậc của nó.
Thu gọn rồi tính giá trị của mỗi đơn thức sau:
a) \(A = \left( { - 2} \right){x^2}y\dfrac{1}{2}xy\) khi \(x = - 2;y = \dfrac{1}{2}.\)
b) \(B = xyz\left( { - 0,5} \right){y^2}z\) khi \(x = 4;y = 0,5;z = 2.\)
Em hãy viết ra hai đơn thức tùy ý (không chứa biến, hoặc chứa từ một đến ba biến trong các biến x,y,z) rồi trao đổi với bạn ngồi cạnh để kiểm tra xem đã viết đúng chưa. Nếu chưa đúng, hãy cùng bạn sửa lại cho đúng.
Đơn thức \( - {2^3}{x^2}y{z^3}\) có:
A. Hệ số -2, bậc 8
B. Hệ số \( - {2^3}\), bậc 5
C. Hệ số -1, bậc 9
D. Hệ số \( - {2^3}\), bậc 6
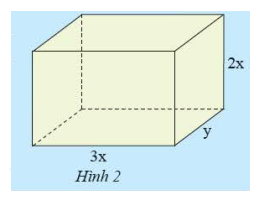
Để tính thể tích của hình hộp chữ nhật ở hình 2, bạn An viết \(V = 3xy.2x\), còn bạn Tâm viết \(V = 6{x^2}y\). Nêu nhận xét về kết quả của hai bạn.
Thu gọn các đơn thức sau đây. Chỉ ra hệ số và bậc của chúng.
a) \(12x{y^2}x\)
b) \( - y\left( {2z} \right)y\)
c) \({x^3}yx\)
d) \(5{x^2}{y^3}{z^4}y\)
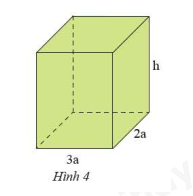
Cho hình hộp chữ nhật có các kịch thước như hình 4 (tính theo cm).
a) Viết các biểu thức tính thể tích và diện tích xung quanh của hình hộp chữ nhật đó.
b) Tính giá trị của các đại lượng trên khi \(a = 2\)cm; \(h = 5\)cm.
Thu gọn các đơn thức sau. Chỉ ra hệ số, phần biến và bậc của mỗi đơn thức.
\(5xyx\); \( - xyz\dfrac{2}{3}y\); \( - 2{x^2}\left( { - \dfrac{1}{6}} \right)x\)
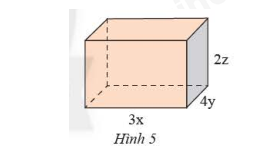
Viết biểu thức biểu thị thể tích \(V\) và diện tích xung quanh \(S\) của hình hộp chữ nhật trong Hình \(5\).
Tính giá trị của \(V\), \(S\) khi \(x = 4\)cm; \(y = 2\)cm và \(z = 1\)cm.
a) Viết biểu thức biểu thị:
- Diện tích của hình vuông có độ dài cạnh là x (cm)
- Diện tích hình chữ nhật có độ dài hai cạnh lần lượt là 2x (cm), 3y (cm)
- Thể tích của hình hộp chữ nhật có ba kích thước lần lượt là x (cm), 2y (cm), 3z (cm).
b) Cho biết mỗi biểu thức trên gồm những số, biến và phép tính nào.
Trong các biểu thức sau, biểu thức nào là đơn thức: \(5y;y + 3{\rm{z}};\dfrac{1}{2}{x^3}{y^2}{x^2}z\)
Xét đơn thức \(2{{\rm{x}}^3}{y^4}\). Trong các đơn thức này, biến x, y được viết bao nhiêu lần dưới dạng một lũy thừa với số mũ nguyên dương.
Thu gọn mỗi đơn thức sau: \({y^3}{y^2}z\);\(\dfrac{1}{3}x{y^2}{x^3}z\)
Cho hai đơn thức: \(2{{\rm{x}}^3}{y^4}\) và \( - 3{{\rm{x}}^3}{y^4}\)
a) Nêu hệ số của mỗi đơn thức trên.
b) So sánh phần biến của hai đơn thức trên
Thu gọn mỗi đơn thức sau:
a) \( - \dfrac{1}{2}{x^2}yx{y^3}\)
b) \(0,5{{\rm{x}}^2}{\rm{yzx}}{y^3}\)
Cho một ví dụ về đơn thức một biến và một ví dụ về đơn thức năm biến.
Cho đơn thức \(3x{y^4}z{x^2}y{z^3}\)
a) Ta đã sử dụng các tính chất nào của phép nhân các số để suy ra
\(3x{y^4}z{x^2}y{z^3} = 3x{x^2}{y^4}yz{z^3}\)
b) Dựa vào quy tắc nhân hai lũy thừa cùng cơ số, hãy tìm các số mũ thích hợp cho các ô trong đẳng thức sau:
c) So sánh tổng số mũ của tất cả các biến có trong đơn thức \(3x{y^4}z{x^2}y{z^3}\) với tổng số cũ của tất cả các biến có trong đơn thức ở vế phải của đẳng thức trong câu b.
Cho ba ví dụ về đơn thức thu gọn và cho biết hệ số, phần biến và bậc của đơn thức thu gọn trong mỗi ví dụ.
Bạn Thảo viết sáu ví dụ về đơn thức như sau:
\(4{x^3}\); \( - x{y^2}\); \(\frac{2}{9}\); \(6{x^2}\left( {x - 1} \right)\); \( - 9\left( {x + y} \right)\); \(27{x^3}{y^3}z\).
Hãy kiểm tra xem bạn Thảo đã viết đúng chưa.
Trong các biểu thức sau, biểu thức nào là đơn thức?
a) Biểu thức biểu diễn chu vi \(\left( m \right)\) của khu vườn hình chữ nhật có chiều dài và chiều rộng lần lượt là \(x\left( m \right)\) và \(y\left( m \right)\).
b) Biểu thức biểu diễn diện tích \(\left( {{m^2}} \right)\) của khu vườn hình chữ nhật có chiều dài và chiều rộng lần lượt là \(x\left( m \right)\) và \(y\left( m \right)\).
Thu gọn đơn thức rồi xác định hệ số, phần biến và bậc của đơn thức thu gọn.
a) \( - 3{x^2}{y^2}7{x^3}y;\)
b) \(\frac{3}{4}xy\frac{8}{9}yz6xy\)
Thu gọn rồi tìm hệ số và bậc của mỗi đơn thức sau:
\(3x{y^2}{x^2}\sqrt 5 \); \( - 7,5xz( - 2)yz\); \(x(1 + \pi )xy\); \(\frac{{y{x^2}}}{3}y{z^2}\).
Thu gọn rồi tính giá trị của mỗi đơn thức sau tại giá trị đã cho của các biến:
a) \(M = \frac{1}{2}{x^2}y( - 4)y\) khi \(x = \sqrt 2 \), \(y = \sqrt 3 \).
b) \(N = xy\sqrt 5 {x^2}\) khi \(x = - 2\), \(y = \sqrt 5 \).
