Đâu là tính chất đúng của phân thức đại số?
-
A.
\(\frac{A}{B} = \frac{{A \cdot M}}{{B \cdot M}}\,\,\left( {B,M \ne 0} \right)\).
-
B.
\(\frac{A}{B} = \frac{{A \cdot M}}{B}\,\,\left( {B,M \ne 0} \right)\).
-
C.
\(\frac{A}{B} = \frac{A}{{B \cdot M}}\,\,\left( {B,M \ne 0} \right)\).
-
D.
\(\frac{A}{B} = \frac{{A \cdot M}}{{B \cdot N}}\,\,\left( {B,M \ne 0,N \ne M} \right)\).
Tính chất của phân thức đại số: Nếu nhân cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức 0 thì được một phân thức mới bằng phân thức đã cho.
\(\frac{A}{B} = \frac{{A.M}}{{B.M}}\left( {M \ne 0} \right)\)
Với \(B,M \ne 0\) ta có: \(\frac{A}{B} = \frac{{A.M}}{{B.M}}.\)
Đáp án A.
Đáp án : A
Các bài tập cùng chuyên đề
Xét hai phân thức \(M = \dfrac{x}{y}\) và \(N = \dfrac{{{x^2} + x}}{{xy + y}}\)
a) Tính giá trị của các phân thức trên khi \(x = 3\), \(y = 2\) và khi \(x = - 1\), \(y = 5\).
Nêu nhận xét về giá trị của \(M\) và \(N\) khi cho \(x\) và \(y\) nhận những giá trị nào đó (\(y \ne 0\) và \(xy - y \ne 0\)).
b) Nhân tử thức của phân thức này với mẫu thức của phân thức kia, rồi so sánh hai đa thức nhận được.
Mỗi cặp phân thức sau đây có bằng nhau không? Tại sao?
a) \(\dfrac{{x{y^2}}}{{xy + y}}\) và \(\dfrac{{xy}}{{x + 1}}\)
b) \(\dfrac{{xy - y}}{x}\) và \(\dfrac{{xy - x}}{y}\)
a) Tính số thích hợp vào ?: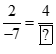 
; 
b) Hãy nhắc lại tính chất cơ bản của phân số.
Dùng tính chất cơ bản của phân thức, hãy giải thích vì sao có thể viết: \(\dfrac{{3{\rm{x}} + y}}{y} = \dfrac{{3{\rm{x}}y + {y^2}}}{{{y^2}}}\)
a) Cho phân thức \(\frac{{2x}}{7}\). Hãy nhân cả tử và mẫu của phân thức này với \(3{x^2}\) rồi so sánh phân thức vừa nhận được với phân thức đã cho.
b) Cho phân thức \(\frac{{15{x^3}{y^2}}}{{25{x^2}{y^3}}}\). Hãy chia cả tử và mẫu của phân thức này cho \(5{x^2}{y^2}\) rồi so sánh phân thức vừa nhận được với phân thức đã cho.
Tìm một đa thức thích hợp cho ô ? để có hai phân thức bằng nhau: \(\frac{{5x - 1}}{{6x - 7}} = \frac{?}{{6{x^2} - 7x}}\).
Dùng tính chất cơ bản của phân thức, hãy chứng minh:
a) \(\frac{{4 - x}}{{ - 2x}} = \frac{{x - 4}}{{2x}}\)
b) \(\frac{{{x^4}{y^3}{z^2}}}{{{x^2}{y^3}{z^4}}} = \frac{{{x^2}}}{{{z^2}}}\)
c) \(\frac{{y - x}}{{3 - x}} = \frac{{x - y}}{{x - 3}}\)
d) \(\frac{{x + y}}{x} = \frac{{{x^2} - {y^2}}}{{x\left( {x - y} \right)}}\)
Liệu phân thức nào đơn giản nhưng bằng phân thức \(\frac{{x - y}}{{{x^3} - {y^3}}}\) không nhỉ?
Nếu nhân cả tử và mẫu của phân thức \(\frac{{x + y}}{{x - y}}\) với 2x ta được phân thức mới nào? Giải thích vì sao phân thức mới nhận được bằng phân thức đã cho.
Khẳng định sau đúng hay sai? Vì sao?
\(\frac{{30{\rm{x}}{y^2}\left( {x - y} \right)}}{{45{\rm{x}}y{{\left( {x - y} \right)}^2}}} = \frac{{2y}}{{3\left( {x - y} \right)}}\)
Giải thích vì sao \(\frac{{ - x}}{{1 - x}} = \frac{x}{{x - 1}}\)
Liệu phân thức nào đơn giản nhưng bằng phân thức \(\frac{{x - y}}{{{x^3} - {y^3}}}\) không nhỉ?
Dùng tính chất cơ bản của phân thức, giải thích vì sao các kết luận sau đúng.
\(a)\frac{{{{\left( {x - 2} \right)}^3}}}{{{x^2} - 2}} = \frac{{{{\left( {x - 2} \right)}^2}}}{2}\)
\(b)\frac{{1 - x}}{{ - 5{\rm{x}} - 1}} = \frac{{x - 1}}{{5{\rm{x}} - 1}}\)
Tìm đa thức thích hợp thay cho dấu: “?”: \[\frac{{y - x}}{{4 - x}} = \frac{?}{{x - 4}}\]
Tìm a sao cho hai phân thức sau bằng nhau:
\(\frac{{5{\rm{x}}}}{{x + 1}}\) và \(\frac{{ax\left( {x - 1} \right)}}{{\left( {1 - x} \right)\left( {x + 1} \right)}}\)
Phân thức \(\frac{{1 - x}}{{y - x}}\) bằng với phân thức nào sau đây?
Chọn cách viết đúng.
Sử dụng quy tắc đổi dấu, ta đưa phân thức \(\frac{{ - x - y}}{6}\) về dạng phân thức nào sau đây?
Dùng tính chất cơ bản của phân thức, chứng minh \(\frac{{{x^4} - 1}}{{x - 1}} = {x^3} + {x^2} + x + 1\)
Sử dụng tính chất cơ bản của phân thức và quy tắc đổi dấu, viết phân thức \(\frac{{24{x^2}{y^2}}}{{3x{y^5}}}\) thành một phân thức có mẫu là \( - {y^3}\) rồi tìm đa thức B trong đẳng thức \(\frac{{24{x^2}{y^2}}}{{3x{y^5}}} = \frac{B}{{ - {y^3}}}\)
Dùng tính chất cơ bản của phân thức, giải thích vì sao các kết luận sau đúng.
a) \(\frac{{{{(x - 2)}^3}}}{{{x^2} - 2x}} = \frac{{{{(x - 2)}^2}}}{x};\)
b) \(\frac{{1 - x}}{{ - 5x + 1}} = \frac{{x - 1}}{{5x - 1}}\).
Tìm đa thức thích hợp thay cho dấu “?”.
\(\frac{{y - x}}{{4 - x}} = \frac{?}{{x - 4}}\)
