Một hồ bơi có dạng tứ giác \(ABCD\) được mô tả như hình vẽ bên. Biết \(AC\) là tia phân giác \(\widehat {BAD}\) và \(\widehat {DAC} = 40^\circ \).
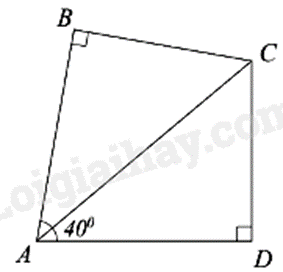
a) Tính \(\widehat {BCD}.\)
b) Biết \(AB = 7,66\) m và \(BC = 6,43\) m. Một vận động viên bơi lội muốn bơi từ \(A\) đến \(C\) trong 20 giây thì cần bơi với vận tốc là bao nhiêu (làm tròn kết quả đến hàng phần mười)?
a) Dựa vào tính chất của tia phân giác để tính góc BAD.
Sử dụng định lí tổng các góc của một tứ giác bẳng \(360^\circ \) để tính góc BCD.
b) Sử dụng định lí Pythagore để tính AC.
Dựa vào kiến thức: quãng đường = vận tốc . thời gian để tính vận tốc của vận động viên.
a) Do \(AC\) là tia phân giác \(\widehat {BAD}\) nên ta có \(\widehat {BAD} = 2\widehat {DAC} = 2 \cdot 40^\circ = 80^\circ \)
Xét tứ giác \(ABCD\) có: \(\widehat {BAD} + \widehat {B\,} + \widehat {BCD} + \widehat {D\,} = 360^\circ \)
Suy ra
\(\widehat {BCD} = 360^\circ - \left( {\widehat {BAD} + \widehat {B\,} + \widehat {D\,}} \right) \\= 360^\circ - \left( {80^\circ - 90^\circ - 90^\circ } \right) = 100^\circ \)
b) Xét \(\Delta ABC\) vuông tại \(B\), theo định lí Pythagore ta có:
\(A{C^2} = A{B^2} + B{C^2} = 7,{66^2} + 6,{43^2} = 100,0205\)
Suy ra \(AC = \sqrt {100,0205} \approx 10,0\) m.
Khi đó vận động viên cần bơi với vận tốc là \(\frac{{10,0}}{{20}} = 0,5\) (m/s).

Các bài tập cùng chuyên đề
Bài 1 :
Tam giác \(DEF\) vuông tại \(D\) có \(DE = 5cm,{\rm{ }}EF = 13cm\) khi đó số đo cạnh DF bằng:
-
A.
\(15cm\)
-
B.
\(8cm\)
-
C.
\(10cm\)
-
D.
\(12cm\)
Bài 2 :
Tứ giác ABCD có \(\widehat C + \widehat D = {90^o}\) Chọn câu đúng.
-
A.
AC2 + BD2 = AB2 – CD2
-
B.
AC2 + BD2 = AB2 + CD2
-
C.
AC2 + BD2 = 2AB2
-
D.
Cả A, B, C đều sai
Bài 3 :
Cho tam giác ABC vuông cân ở A. Tính độ dài BC biết AB = AC = 2 dm
-
A.
BC = 4 dm.
-
B.
\(BC = \sqrt {64} dm\).
-
C.
BC = 8 dm.
-
D.
\(BC = \sqrt 8 dm\)
Bài 4 :
Cho hình vẽ. Tính x.
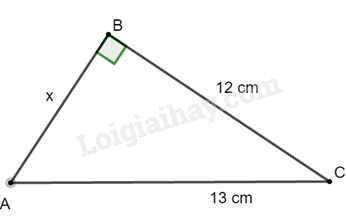
-
A.
x = 10 cm.
-
B.
x = 11 cm.
-
C.
x = 8 cm.
-
D.
x = 5 cm
Bài 5 :
Một tam giác vuông có cạnh huyền bằng 26cm độ dài các cạnh góc vuông tỉ lệ với 5 và 12. Tính độ dài các cạnh góc vuông.
-
A.
12cm ; 24cm.
-
B.
10cm ; 22 cm.
-
C.
10cm ; 24cm.
-
D.
15cm ; 24cm.
Bài 6 :
Cho hình vẽ sau. Tính \(x\).
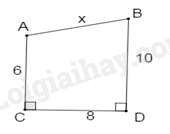
-
A.
\(5\).
-
B.
\(5\sqrt 4 \).
-
C.
\(4\).
-
D.
\(4\sqrt 5 \).
Bài 7 :
Cạnh huyền của một tam giác là bao nhiêu biết hai cạnh góc vuông là 3 và 4.
-
A.
8
-
B.
7
-
C.
6
-
D.
5
Bài 8 :
Cho tam giác ABC vuông cân ở A. Tính độ dài BC biết AB = AC = 4 dm
-
A.
BC = 6 dm.
-
B.
BC = 4 dm.
-
C.
\(BC = \sqrt {23} dm\).
-
D.
\(BC = \sqrt {32} dm\).
Bài 9 :
Cho hình vẽ. Tính x:
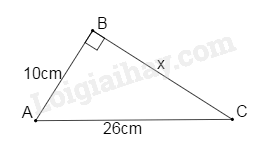
-
A.
x = 22cm.
-
B.
x = 32 cm.
-
C.
x = 20cm.
-
D.
x = 24 cm.
Bài 10 :
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H. Cho BH = 2cm, AB = 4cm. Tính AH:
-
A.
\(\sqrt {10} cm\).
-
B.
\(\sqrt {13} cm\).
-
C.
\(\sqrt {12} cm\).
-
D.
12 cm.
Bài 11 :
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H. Cho BH = 5cm , AB = 13cm. Tính diện tích tam giác ABC:
-
A.
\(12 cm^2\).
-
B.
\(36 cm^2\).
-
C.
\(40 cm^2\).
-
D.
\(60 cm^2\).
Bài 12 :
Cho ABCD là hình vuông cạnh 4 cm (hình vẽ). Khi đó độ dài đường chéo AC là:
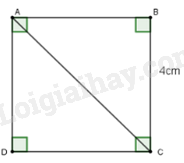
-
A.
\(AC = 4\sqrt 2 cm\).
-
B.
\(AC = 4cm\).
-
C.
\(AC = \sqrt {30} cm\).
-
D.
\(AC = 8cm\).
Bài 13 :
Một tam giác vuông có độ dài cạnh huyền bằng 20 cm, độ dài các cạnh góc vuông tỉ lệ với 3 và 4. Tính độ dài các cạnh góc vuông.
-
A.
9cm; 12cm.
-
B.
10cm; 16 cm.
-
C.
12cm; 16cm.
-
D.
12cm ; 14cm
Bài 14 :
Cho tam giác ABC vuông ở A có AC = 20 cm. Kẻ \(AH \bot BC\). Biết BH = 9cm; HC = 16cm. Tính AB , AH
-
A.
AH = 12cm; AB = 15cm.
-
B.
AH = 10cm; AB = 15 cm.
-
C.
AH = 15cm; AB = 12cm.
-
D.
AH = 12cm; AB = 13 cm.
Bài 15 :
Cho tam giác ABC. Kẻ AH vuông góc với BC. Tính chu vi tam giác ABC biết AB = 5cm, AH = 4 cm, \(HC = \sqrt {184} cm\). (làm tròn đến chữ số thập phân thứ nhất).
-
A.
30,8cm.
-
B.
35, 7cm.
-
C.
31 cm.
-
D.
31, 7cm.
Bài 16 :
Cho hình vẽ sau. Tính x.
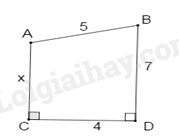
-
A.
6.
-
B.
3.
-
C.
5.
-
D.
4.
Bài 17 :
Tính cạnh huyền của một tam giác vuông biết tỉ số các cạnh góc vuông là 3 : 4 và chu vi tam giác là 36 cm
-
A.
9cm.
-
B.
12cm .
-
C.
15cm.
-
D.
16cm.
Bài 18 :
Tìm x trong hình vẽ sau:
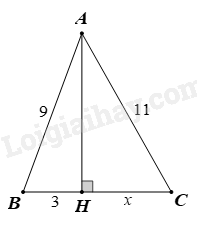
-
A.
x = 6
-
B.
x = 7
-
C.
x = 8
-
D.
x = 5
Bài 19 :
Tìm x trong hình vẽ sau:
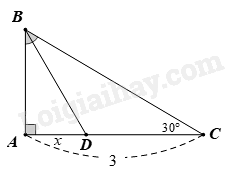
-
A.
x = 2
-
B.
x = 1,5
-
C.
x = 1
-
D.
x = 1,2
Bài 20 :
Tìm câu trả lời sai. Cho hình vẽ biết DE // HK. Khi đó:
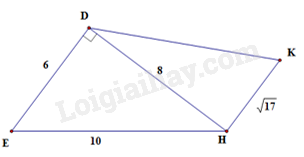
-
A.
DK = 9
-
B.
\(\widehat {E{{D}}H} = {90^o}\)
-
C.
DK = 10
-
D.
\(\widehat {DHK} = {90^o}\)
Bài 21 :
Cho tam giác ABC biết BC = 7,5cm; CA = 4,5cm, AB = 6cm. Độ dài đường cao AH của tam giác ABC là:
-
A.
12,96cm
-
B.
6,48cm
-
C.
3,6cm
-
D.
6,3cm
Bài 22 :
Cho tam giác ABC cân tại A biết AB = AC = 17cm. Kẻ \(B{\rm{D}} \bot AC\), biết BD = 15cm. Tính cạnh đáy BC.
-
A.
17 cm
-
B.
16 cm
-
C.
\(3\sqrt {14} \)cm
-
D.
\(3\sqrt {34} cm\)
Bài 23 :
Tính x trong hình sau:
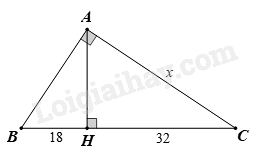
-
A.
36
-
B.
40
-
C.
42
-
D.
30
Bài 24 :
Cho một tam giác vuông có hai cạnh góc vuông là \(a\), \(b\) và cạnh huyền là \(c\).
- Lấy một tờ bìa lớn, cắt tám hình tam giác vuông bằng tam giác vuông đã cho và cắt hai hình vuông lớn có cùng có cạnh bằng \(a + b\).
- Đặt bốn tam giác vuông lên hình vuông thứ nhất trong Hình 1a. Phần bìa không bị che lấp gồm hai hình vuông có cạnh lần lượt là \(a\) và \(b\). Tính diện tích phần bìa đó là \(a\) và \(b\).
- Đặt bốn tam giác vuông còn lại lên hình vuông thứ hai như trong Hình 1b. Phần bìa không bị che lấp là hình vuông có cạnh là \(c\). Tính diện tích phần bìa đó theo \(c\).
- Rút ra kết luận về quan hệ giữa \({a^2} + {b^2}\) và \({c^2}\).

Bài 25 :
Tính độ dài cạnh \(EF\), \(MN\) của các tam giác vuông trong hình 3.
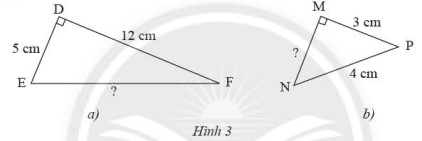
Bài 26 :
Một chiếc ti vi màn hình phẳng có chiều rộng và chiều dài đo được lần lượt là \(72\)cm và \(120\)cm. Tính độ dài đường chéo của màn hình chiếc ti vi đó theo đơn vị inch (biết 1 inch \( \approx \)\(2,54\)cm).

Bài 27 :
a) Nam dự định làm một cái êke từ ba thanh nẹp gỗ. Nam đã có hai thanh làm hai cạnh góc vuông dài \(6\)cm và \(8\)cm. Hỏi thanh nẹp còn lại Nam phải làm có độ dài bao nhiêu? (Giả sử các mối nối không đáng kể).
b) Một khung gỗ \(ABCD\) (Hình 6) được tạo thành từ \(5\) thanh nẹp có độ dài như sau: \(AB = CD = 36\)cm; \(BC = AD = 48\)cm; \(AC = 60\)cm. Chứng minh rằng \(\widehat {ABC}\) và \(\widehat {ADC}\) là các góc vuông.

Bài 28 :
Cho tam giác \(ABC\) vuông tại \(A\).
a) Tính độ dài cạnh \(BC\) nếu biết \(AB = 7\)cm, \(AC = 24\)cm.
b) Tính độ dài cạnh \(AB\) biết \(AC = 2\)cm, \(BC = \sqrt {13} \)cm.
c) Tính độ dài cạnh \(AC\) nếu biết \(BC = 25\)cm, \(AB = 15\)cm.
Bài 29 :
Lần lượt tính độ dài các cạnh huyền \(a\), \(b\), \(c\), \(d\) của các tam giác vuông trong Hình 12. Hãy dự đoán kết quả của các cạnh huyền còn lại.
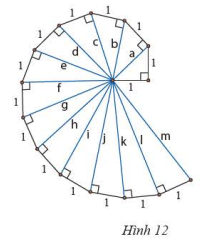
Bài 30 :
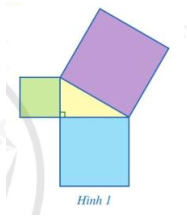
Quan sát Hình 1, bạn Đan khẳng định: Diện tích của hình vuông lớn nhất bằng tổng diện tích của hai hình vuông còn lại.
Bạn Đan đã dựa vào kiến thức nào để đưa ra khẳng định trên?


















Danh sách bình luận