Gieo hai con xúc xắc cân đối. Hãy so sánh xác suất xảy ra của các biến cố sau:
A: “Tổng số chấm xuất hiện ở mặt trên hai con xúc xắc là số chẵn”,
B: “Số chấm xuất hiện ở mặt trên hai con xúc xắc đều bằng 6”,
C: “Số chấm xuất hiện ở mặt trên hai con xúc xắc bằng nhau".
Ta tính xác suất xảy ra các biến cố A,B,C sau đó so sánh các biến cố
Tổng số chấm xuất hiện ở mặt trên hai con xúc xắc chỉ có thể là số chẵn hoặc số lẻ nên \(P(A) = \frac{1}{2}\).
Số chấm xuất hiện ở mặt trên một con xúc xắc bằng 6 có xác suất xuất hiện là \(\frac{1}{6}\).
Do đó số chấm xuất hiện ở mặt trên hai con xúc xắc đều bằng 6 có xác suất xuất hiện là \(\frac{1}{6}.\frac{1}{6}=\frac{1}{36}\) hay \(P(B) =\frac{1}{36}\).
Có 6 trường hợp số chấm xuất hiện ở mặt trên hai con xúc xắc bằng nhau tức mặt trên hai con xúc xắc cùng xuất hiện 1 chấm, 2 chấm, 3 chấm, 4 chấm, 5 chấm hoặc 6 chấm.
Vì xác suất xuất hiện số chấm ở mặt trên hai con xúc xắc đều bằng 6 là \(\frac{1}{36}\) nên \(P(C) = 6 . \frac{1}{36} = \frac{1}{6}\).
Ta thấy \(\frac{1}{2}>\frac{1}{6}>\frac{1}{36}\) nên P(A) > P(B) > P(C).

Các bài tập cùng chuyên đề
Bài 1 :
2 biến cố nào sau là 2 biến cố đồng khả năng?
-
A.
“ Lượng mưa tháng 6 tại Hà Nội là 800 mm” và “ Lượng mưa tháng 7 tại Hà Nội là 800 mm”
-
B.
“ Tung 1 đồng xu xuất hiện mặt sấp” và “ Tung 1 đồng xu xuất hiện mặt ngửa”
-
C.
Viết 1 số tự nhiên bất kì. Hai biến cố là “ Viết được số nguyên tố” và “ Viết được hợp số”
-
D.
Lớp 7A2 có 15 học sinh nam, 31 học sinh. Cô giáo gọi ngẫu nhiên 1 bạn lên làm bài tập. 2 biến cố “Cô gọi được bạn nam ” và “ Cô gọi được bạn nữ”
Bài 2 :
Cho trò chơi Ô cửa bí mật, có ba ô cửa 1,2,3 và người ta đặt phần thưởng sau một ô cửa. Người chơi sẽ chọ ngẫu nhiên một ô cửa trong ba ô cửa và nhận phần thưởng sau ô cửa đó. Tìm xác suất để người chơi chọn được ô cửa có phần thưởng
Bài 3 :
Gieo một con xúc xắc được chế tạo cân đối.
Tìm xác suất để số chấm xuất hiện trên con xúc xắc là 2.
Bài 4 :
Trước trận chung kết bóng đá World Cup năm 2010 giữa hai đội Hà Lan và Tây Ban Nha, để dự đoán kết quả người ta bỏ cùng loại thức ăn vào hai hộp giống nhau, một hộp có gắn cờ Hà Lan, một hộp gắn cờ Tây Ban Nha và cho Paul chọn hộp thức ăn. Người ta cho rằng nếu Paul chọn hộp gắn cờ nước nào thì đội bóng nước đó thắng. Paul chọn ngẫu nhiên một hộp. Tính xác suất để Paul dự đoán đội Tây Ban Nha thắng.
Bài 5 :
Một tổ học sinh của lớp 7B có 5 bạn nam và 5 bạn nữ. Giáo viên gọi ngẫu nhiên một bạn lên bảng để kiểm tra bài tập. Xét hai biến cố sau:
A: “ Bạn được gọi là nam”
B: “ Bạn được gọi là nữ”
a) Hai biến cố A và B có đồng khả năng không?
b) Tìm xác suất của biến cố A và biến cố B
Bài 6 :
Trong một chiếc hộp có 15 quả cầu xanh, 15 quả cầu đỏ. Lấy ngẫu nhiên một quả cầu từ trong hộp. Xét hai biến cố sau:
A: “ Lấy được quả cầu màu đỏ” và B: “ Lấy được quả cầu màu xanh”
a) Hai biến cố A và B có đồng khả năng không?
b) Tìm xác suất của biến cố A và biến cố B
Bài 7 :
Một tấm bìa cứng hình tròn được chia làm 8 phần có diện tích bằng nhau và ghi số 1;2;3;4;5;6;7;8 như Hình 8.4, được gắn vào trục quay có mũi tên ở tâm.
Bạn Việt quay tấm bìa.
a) Tìm xác suất để mũi tên chỉ vào hình quạt:
* Ghi số lẻ * Ghi số 6
b) Biết rằng nếu mũi tên dừng ở hình quạt ghi số 1 hoặc 2 thì Việt nhận được 100 điểm; dừng ở hình quạt ghi số 3 hoặc 4 thì Việt nhận được 200 điểm; dừng ở hình quạt ghi số 5 hoặc 6 thì Việt nhận được 300 điểm; dừng ở hình quạt ghi số 7 hoặc 8 thì Việt nhận được 400 điểm.
Xét các biến cố sau:
A: “ Việt nhận được 100 điểm”
B: “ Việt nhận được 200 điểm”
C: “ Việt nhận được 300 điểm”
D: “ Việt nhận được 400 điểm”
- Các biến cố A,B,C,D có đồng khả năng hay không?
- Tìm xác suất các biến cố A,B,C và D.
Bài 8 :
Gieo một con xúc xắc cân đối. Hãy so sánh xác suất của các biến cố sau:
A: “Mặt xuất hiện có 2 chấm”
B: “Mặt xuất hiện có 3 chấm”
Bài 9 :
Một bình có bốn quả bóng có kích thước và khối lượng giống nhau trong đó có 1 quả màu xanh, 1 quả màu vàng, 1 quả màu đỏ và 1 quả màu trắng. Lấy ra ngẫu nhiên một quả bóng từ bình. Hãy liệt kê các kết quả có thể xảy ra
Bài 10 :
Tính xác suất giành phần thắng của bạn An và bạn Bình trong trò chơi ở trang 90.
Bài 11 :
Một hộp có 10 lá thăm có kích thước giống nhau và được đánh số từ 1 đến 10. Lấy ngẫu nhiên một lá thăm từ hộp.
a) Hãy nêu các điểm cần lưu ý khi tính xác suất liên quan đến hoạt động trên.
b) Gọi A là biến cố : “Lấy được lá thăm ghi số 9”. Hãy tính xác suất của biến cố A.
c) Gọi B là biến cố : “Lấy được lá thăm ghi số nhỏ hơn 11”. Hãy tính xác suất của biến cố B.
Bài 12 :
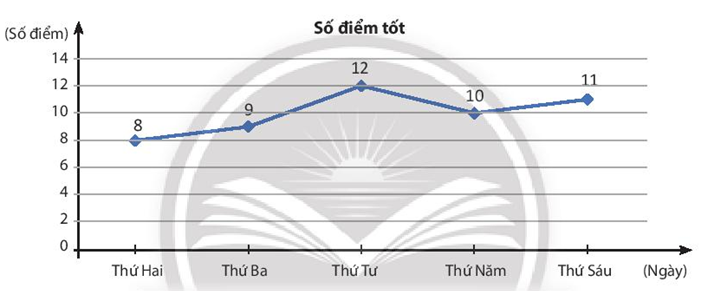
Số điểm tốt các bạn học sinh lớp 7B đạt được trong một tuần được cho ở biểu đồ đoạn thẳng sau. Chọn ngẫu nhiên một ngày trong tuần. Biết rằng khả năng cả 5 ngày được chọn đều như nhau. Tính xác suất của biến cố:
a) ''Vào ngày được chọn các học sinh lớp 7B đạt 10 điểm tốt ''
b) ''Vào ngày được chọn các học sinh lớp 7B đạt ít nhất 8 điểm tốt"
Bài 13 :
Biểu đồ dưới đây thống kê số học sinh Trung học cơ sở của tỉnh Phú Thọ giai đoạn từ năm 2010 đến năm 2019.
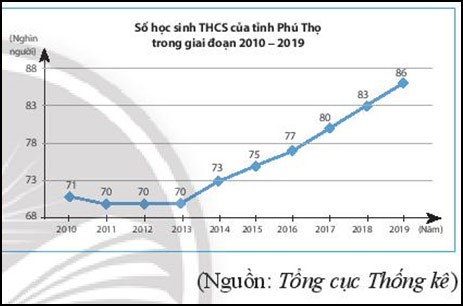
Chọn ngẫu nhiên một năm trong giai đoạn đó. Biết khả năng chọn mỗi năm là như nhau
a) Nêu tập hợp các kết quả có thể xảy ra với năm được chọn.
b) Gọi B là biến cố: "Tỉnh Phú Thọ có trên 85000 học sinh Trung học cơ sở trong năm được chọn". Hãy tính xác suất của biến cố.
Bài 14 :
Gieo ngẫu nhiên xúc xắc một lần. Tỉnh xác suất của mỗi biến cố sau:
a) “Mặt xuất hiện của xúc xắc có số chấm là số lẻ và chia hết cho 3”
b) “Mặt xuất hiện của xúc xắc có số chấm là số chia 5 dư 2”
Bài 15 :
Một hộp có 60 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2 3, ..., 59, 60; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tìm số phần tử của tập hợp C gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra. Sau đó, hãy tính xác suất của mỗi biến cố sau:
a) “Số xuất hiện trên thẻ được rút ra là số có hai chữ số lớn hơn 25”
b) “Số xuất hiện trên thẻ được rút ra là số chia hết cho 7”
c) “Số xuất hiện trên thẻ được rút ra là số chia hết cho cả 3 và 5”
d) “Số xuất hiện trên thẻ được rút ra là số có chữ số hàng chục gấp hai lần chữ số hàng đơn vị”
Bài 16 :
Danh sách đội dự thi trực tuyến về “An toàn giao thông” của học sinh lớp 7A được đánh số thứ tự từ 1 đến 25, trong đó bạn Minh có số thứ tự là 15. Chọn ngẫu nhiên một học sinh trong đội đó. Tìm số phần tử của tập hợp D gồm các kết quả có thể xảy ra đối với số thứ tự của học sinh được chọn ra. Sau đó, hãy tính xác suất của mỗi biến cố sau:
a) “Số thứ tự của học sinh được chọn ra là số thứ tự của bạn Minh”
b) “Số thứ tự của học sinh được chọn ra nhỏ hơn số thứ tự của bạn Minh”
Bài 17 :
Viết ngẫu nhiên một số tự nhiên có hai chữ số lớn hơn 40. Tìm số phần tử của tập hợp M gồm các kết quả có thể xảy ra đối với số tự nhiên được viết ra. Sau đó, hãy tính xác suất của mỗi biến cố sau:
a) “Số tự nhiên được viết ra là bội của 9”
b) “Số tự nhiên được viết ra là ước chung của 200 và 300”
c) “Số tự nhiên được viết ra có tổng các chữ số hàng chục và hàng đơn vị bằng 9”
d) “Số tự nhiên được viết ra là tổng của hai số tự nhiên liên tiếp”
Bài 18 :
Một đội tình nguyện tham gia chống dịch Covid-19 gồm 26 thành viên đến từ các tỉnh: Điện Biên, Hà Giang, Sơn La, Lai Châu, Hà Nội, Thái Bình, Vĩnh Phúc, Hưng Yên, Nam Định, Hải Dương, Hải Phòng, Ninh Bình, Gia Lai, Kon Tum, Đắk Lắc, Đắc Nông, Lâm Đồng, Cần Thơ, Long An, Bến Tre, Trà Vinh, Hậu Giang, Kiên Giang, Bạc Liêu, Cà Mau, Đồng Tháp; mỗi tỉnh chỉ có đúng một thành viên trong đội. Chọn ngẫu nhiên một thành viên của đội tinh nguyện đó. Tìm số phần tử của tập hợp G gồm các kết quả có thể xảy ra đối với thành viên được chọn ra. Sau đó, hãy tính xác suất của mỗi biến cổ sau
a) “Thành viên được chọn ra đến từ vùng Trung du và miền núi phía Bắc”
b) “Thành viên được chọn ra đến từ vùng Đồng bằng sông Hồng”
c) “Thành viên được chọn ra đến từ vùng Tây Nguyên”
d) “Thành viên được chọn ra đến tử vùng Đồng bằng sông Cửu Long”
Bài 19 :
Một hộp có 50 chiếc thẻ củng loại, mỗi thẻ được ghi một trong các số 150, 151. 152, ..., 198, 199; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là số có tổng ba chữ số bằng 12” là:
A. \(\frac{2}{{25}}\)
B. \(\frac{7}{{50}}\)
C. \(\frac{4}{{25}}\)
D. \(\frac{1}{{10}}\)
Bài 20 :
Gieo ngẫu nhiên xúc xắc một lần. Tính xác suất của mỗi biến cố sau:
a) “Mặt xuất hiện của xúc xắc có số chấm là ước số của 5”
b) “Mặt xuất hiện của xúc xắc có số chấm là số chẵn không chia hết cho 4”
Bài 21 :
Một hộp có 50 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, ..., 49, 50; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố sau:
a) “Số xuất hiện trên thẻ được rút ra là số lớn hơn 25”
b) “Số xuất hiện trên thẻ được rút ra là số có chứa chữ số 3”
c) “Số xuất hiện trên thẻ được rút ra là số khi chia cho 11 dư 2 và chia cho 5 dư 3”
Bài 22 :
Một hộp có 10 quả bóng được đánh số từ 1 đến 10, đồng thời các quả bóng từ 1 đến 6 được sơn màu vàng và các quả bóng còn lại được sơn màu xanh, các quả bóng có kích thước và khối lượng như nhau. Lấy ngẫu nhiên một quả bóng trong hộp. Tính xác suất của mỗi biển cổ sau
a) “Quả bóng được chọn ra màu vàng”
b) “Quả bóng được chọn ra màu xanh”
c) “Quả bóng được chọn ra ghi số chẵn”
d) “Quả bóng được chọn ra màu vàng và ghi số chẵn”
Bài 23 :
Một câu lạc bộ ngoại ngữ có 60 học sinh trong đó có 40 học sinh học tiếng Anh, 30 học sinh học tiếng Pháp, 20 học sinh học cả tiếng Anh và tiếng Pháp. Chọn ngẫu nhiên một học sinh trong câu lạc bộ. Tinh xác suất của các biến cố sau:
a) “Học sinh được chọn học tiếng Anh”;
b) “Học sinh được chọn học tiếng Pháp”;
c) “Học sinh được chọn học cả tiếng Anh và tiếng Pháp”
Bài 24 :
Tại một hội thảo có 50 đại biểu trong đó có 25 đại biểu nam. Phóng viên chọn ngẫu nhiên một đại biểu để phỏng vấn. Tính xác suất để đại biểu được chọn phỏng vấn là nữ.
Bài 25 :
Một túi đựng tám quả cầu được ghi các số 12; 18; 20; 22; 24; 26; 30; 34. Lấy ngẫu nhiên một quả cầu trong túi. Tính xác suất để:
a) Lấy được quả cầu ghi số chia hết cho 3;
b) Lấy được quả cầu ghi số chia hết cho 11;
c) Lấy được quả cầu ghi số 12 hoặc 18.
Bài 26 :
Một hộp đựng 20 quả bóng có cùng kích thước, khác nhau về màu sắc trong đó có 4 quả bóng màu xanh, 4 quả bóng màu đỏ, 4 quả bóng màu tím, 4 quả bóng màu vàng và 4 quả bóng màu trắng. Bạn Minh lấy ngẫu nhiên một quả bóng từ trong hộp.
Xét 5 biến cố sau:
A: “Minh lấy được quả bóng màu xanh”
B: “Minh lấy được quả bóng màu đỏ”
C: “Minh lấy được quả bóng màu trắng”
D: “Minh lấy được quả bóng màu vàng”
a) Hãy giải thích vì sao các biến cố A, B, C, D, E là đồng khả năng
b) Tính xác suất các biến cố A, B, C, D, E.
Bài 27 :
Một thùng kín có 40 quả bóng cùng kích thước, một số quả có màu trắng và một số quả có màu đen. Sơn lấy ngẫu nhiên một quả bóng trong thùng. Biết rằng biến cố “Sơn chọn được quả bóng màu trắng” và biến cố “Sơn chọn được quả bóng màu đen” là đồng khả năng. Hỏi trong thùng chứa bao nhiêu quả bóng màu trắng?
Bài 28 :
Một chiếc hộp chứa 50 viên bi cùng kích thước gồm một số viên bi màu xanh; một số viên bi màu đỏ; một số viên bi màu trắng; một số viên bi màu tím và một số viên bi màu vàng. Bạn Bình lấy ngẫu nhiên 1 viên bi trong hộp. Biết rằng 5 biến cố sau đây là đồng khả năng:
A: “Bình lấy được viên bi màu xanh”;
B: “Bình lấy được viên bi màu đỏ”;
C: “Bình lấy được viên bi màu trắng”;
D: “Bình lấy được viên bi màu tím”;
E: “Bình lấy được viên bi màu vàng”.
Hỏi trong hộp chứa bao nhiêu viên bi mỗi loại?
Bài 29 :
Một hộp kín có 20 viên bi trắng, 20 viên bi đen. An lấy ngẫu nhiên một viên bi trong hộp. Xác suất của biến cố “An lấy được viên bi màu đen” bằng
A. 1.
B. 0,5.
C. 0.
D. 0,8.
Bài 30 :
Một chiếc hộp đựng 10 tấm thẻ được ghi số 20; 21; …; 29. Rút ngẫu nhiên một tấm thẻ. Xác suất để tấm thẻ rút được ghi số 21 là
A. \(\frac{1}{{10}}\).
B. \(\frac{1}{9}\).
C. \(\frac{1}{{11}}\).
D. \(\frac{1}{8}\).


















Danh sách bình luận