Lượng điện tiêu thụ mỗi ngày trong 5 ngày đầu tháng 9/2021 của một hộ gia đình được cho ở biểu đồ sau. Chọn ngẫu nhiên một ngày trong 5 ngày đó. Hãy tính xác suất của biến cố: ''Hộ gia đình sử dụng 10 kWh điện trong ngày được chọn''
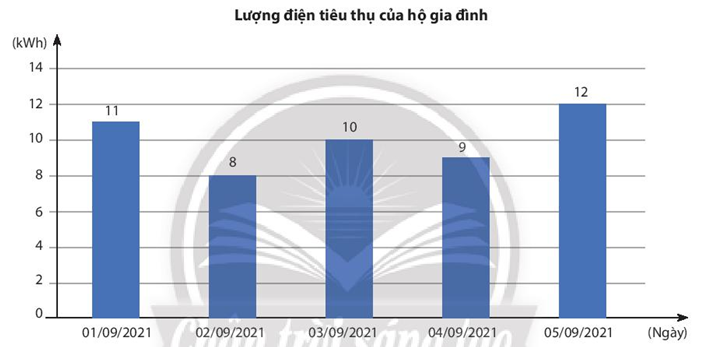
Ta tìm tất cả các ngày có lượng tiêu thụ điện 10kWh sau đó tính xác suất ngày có lượng điện tiêu thụ 10kWh trong 5 ngày đầu tháng 9/2021
Trong 5 ngày đầu tháng 9/2021 dựa vào biểu đồ ta thấy có duy nhất ngày 3/9 có lượng điện tiêu thụ là 10kWh . Nên chọn ngẫu nhiên 1 ngày lượng tiêu thụ điện 10kWh thì xác suất chọn được là \(\dfrac{1}{5}\)

Các bài tập cùng chuyên đề
Bài 1 :
Thực hiện gieo 1 con xúc xắc. Xác suất của biến cố A: “ Số chấm xuất hiện là số nguyên tố” là:
-
A.
\(\dfrac{1}{6}\)
-
B.
1
-
C.
\(\dfrac{1}{3}\)
-
D.
\(\dfrac{1}{2}\)
Bài 2 :
Chọn cụm từ thích hợp ( không thể, ít khả năng, nhiều khả năng, chắc chắn) vào dấu “?” trong các câu sau:
a) Tôi ..?...đi bộ 20 km mà không nghỉ
b) ..?... có tuyết rơi ở Hà Nội vào mùa đông
c) Anh An là một học sinh giỏi. Anh An …?... sẽ đỗ thủ khoa trong kì thi Trung học phổ thông quốc gia tới.
Bài 3 :
Một hộp đựng 20 viên bi, trong đó 13 viên màu đỏ và 7 viên màu đen có cùng kích thước. Bạn Nam lấy ngẫu nhiên một viên bi từ trong hộp. Hỏi khả năng Nam lấy được viên bi màu nào lớn hơn?
Bài 4 :
Hình 8.2 cho biết thông tin dự báo thời tiết tại thành phố Hà Nội trong 5 ngày
Quan sát hình trên, em hãy cho biết ngày nào có khả năng ( hay xác suất) mưa nhiều nhất, ít nhất.
Bài 5 :
Một túi đựng các tấm thẻ được ghi số 9;12;15;21;24. Rút ngẫu nhiên một tấm thẻ trong túi. Chọn từ thích hợp ( chắc chắn, không thể, ngẫu nhiên) thay vào dấu “?” trong các câu sau:
- Biến cố A: “ Rút được thẻ ghi số chẵn” là biến cố …?...
- Biến cố B: “ Rút được thẻ ghi số chia hết cho 3” là biến cố ..?...
- Biến cố C: “ Rút được thẻ ghi số chia hết cho 10” là biến cố ..?...
Bài 6 :
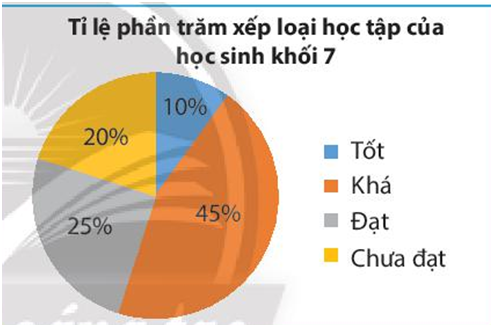
Kết quả xếp loại học tập cuối học kì 1 của học sinh khối 7 được cho ở biểu đồ bên. Gặp ngẫu nhiên một học sinh khối 7
a) Xác xuất học sinh đó được xếp loại học lực nào là cao nhất ?
b) Xác xuất học sinh đó được xếp loại học lực nào là thấp nhất.
Bài 7 :
Gieo một con xúc xắc 6 mặt cân đối. Tính xác suất của các biến cố sau:
A: “Gieo được mặt có số chấm lớn hơn 5”
B: “Gieo được mặt có số chấm nhỏ hơn 7”
Bài 8 :
Một tấm bìa hình tròn được chia thành 6 phần bằng nhau như Hình 1. Bạn Minh đặt tấm bìa nằm thẳng trên bàn, quay mũi tên ở tâm và quan sát xem khi dừng lại thì mũi tên chỉ vào ô nào

Hãy so sánh xác suất xảy ra của các biến cố sau:
A:''Mũi tên chỉ vào ô có màu đỏ''
B:''Mũi tên chỉ vào ô ghi số 3''
C:''Mũi tên chỉ vào ô ghi số lớn hơn 2''
Bài 9 :
Một hộp có chứa 100 chiếc thẻ cùng loại, trong đó chỉ có một thẻ đánh dấu là Thẻ may mắn. Bình lấy ra ngẫu nhiên một thẻ. Tính xác suất biến cố thẻ lấy ra là thẻ may mắn.
Bài 10 :
Gieo một con xúc xắc cân đối. Tính xác suất của các biến cố sau
a) A:''Gieo được mặt có số chấm bằng 4''
b) B:''Gieo được mặt có số chấm chia hết cho 5''
c) C:''Gieo được mặt có số chấm là tròn chục''
Bài 11 :
Đội múa có 1 bạn nam và 5 bạn nữ. Chọn ngẫu nhiên 1 bạn để phỏng vấn. Biết mỗi bạn đều cùng có khả năng được chọn. Hãy tính xác suất của biến cố bạn được chọn là nam.
Bài 12 :
Một hộp có 4 tấm thẻ có kích thước giống nhau và được đánh số lần lượt là 2, 4, 6, 8. Lấy ngẫu nhiên 1 thẻ từ hộp . Hãy tính xác suất của các biến cố sau:
A: “Lấy được thẻ ghi số nguyên tố ''
B: “Lấy được thẻ ghi số lẻ”
C: “Lấy được thẻ ghi số chẵn
Bài 13 :
Một hộp kín chứa 5 quả cầu có kích thước và khối lượng bằng nhau, trong đó có 1 quả màu xanh và 4 quả màu đỏ. Lấy ngẫu nhiên 1 quả cầu từ hộp, tính xác suất của các biến cố sau
A: “Quả cầu lấy ra có màu vàng"
B: "Quả cầu lấy ra có màu xanh’’.
Bài 14 :
Xét một con xúc xắc cân đối và đồng chất một số chấm ở mỗi mặt là một trong các số 1, 2, 3, 4, 5, 6 (Hình 32). Gieo ngẫu nhiên xúc xắc một lần. Khi đó khả năng xuất hiện từ mặt của con xúc xắc là như nhau.
Xét biến cố “Mặt xuất hiện của xúc xắc có số chấm là số lẻ”.
Làm thế nào để phản ánh được khả năng xảy ra của biến cố trên?
Bài 15 :
Gieo ngẫu nhiên xúc xắc một lần. Tính xác suất của biến cố “Mặt xuất hiện của xúc xắc có số chấm là hợp số”.
Bài 16 :
Rút ngẫu nhiên một thẻ trong hộp có 12 chiếc thẻ đã nêu ở Ví dụ 2. Tính xác suất của biến cố “Số xuất hiện trên thẻ rút ra là số không chia hết cho 3”.
Bài 17 :
Gieo ngẫu nhiên xúc xắc một lần. Tính xác suất của mỗi biến cố sau:
a) “Mặt xuất hiện của xúc xắc có số chấm là số nguyên tố”;
b) “Mặt xuất hiện của xúc xắc có số chấm là số chia 4 dư 1”.
Bài 18 :
Một hộp có 52 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, …, 51, 52. Hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tìm số phần tử của tập hợp C gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra. Sau đó, hãy tính xác suất của mỗi biến cố sau:
a) “Số xuất hiện trên thẻ được rút ra là số có một chữ số”;
b) “Số xuất hiện trên thẻ được rút ra là số khi chia cho 4 và 5 đều có số dư là 1”;
c) “Số xuất hiện trên thẻ được rút ra là số có tổng các chữ số bằng 4”.
Bài 19 :
Viết ngẫu nhiên một số tự nhiên có hai chữ số. Tìm số phần tử của tập hợp D gồm các kết quả có thể xảy ra đối với số tự nhiên được viết ra. Sau đó, hãy tính xác suất của mỗi biến cố sau:
a) “Số tự nhiên được viết ra là bình phương của một số tự nhiên”;
b) “Số tự nhiên được viết ra là bội của 15”;
c) “Số tự nhiên được viết ra là ước của 120”.
Bài 20 :
Tổ I của lớp 7D có 5 học sinh nữ là: Ánh, Châu, Hương, Hoa, Ngân và 5 học sinh nam là: Bình, Dũng, Hùng, Huy, Việt. Chọn ra ngẫu nhiên một học sinh trong Tổ I của lớp 7D. Tìm số phần tử của tập hợp E gồm các kết quả có thể xảy ra đối với học sinh được chọn ra. Sau đó, hãy tính xác suất của mỗi biến cố sau:
a) “Học sinh được chọn ra là học sinh nữ”;
b) “Học sinh được chọn ra là học sinh nam”.
Bài 21 :
Một nhóm học sinh quốc tế gồm 9 học sinh đến từ các nước: Việt Nam, Ấn Độ, Ai Cập, Brasil, Canada, Tây Ban Nha, Đức, Pháp, Nam Phi; mỗi nước chỉ có đúng một học sinh. Chọn ra ngẫu nhiên một học sinh trong nhóm học sinh quốc tế trên. Tìm số phần tử của tập hợp G gồm các kết quả có thể xảy ra đối với học sinh được chọn ra. Sau đó, hãy tính xác suất của mỗi biến cố sau:
a) “Học sinh được chọn ra đến từ châu Á”;
b) “Học sinh được chọn ra đến từ châu Âu”;
c) “Học sinh được chọn ra đến từ châu Mỹ”;
d) “Học sinh được chọn ra đến từ châu Phi”;
Bài 22 :
Gieo ngẫu nhiên xúc xắc một lần. Tính xác suất của mỗi biến cố sau:
a) “Mặt xuất hiện của xúc xắc có số chấm là ước của 6”.
b) “Mặt xuất hiện của xúc xắc có số chấm là số chia 3 dư 2”.
Bài 23 :
Một hộp có 52 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, …, 51, 52; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố sau:
a) “Số xuất hiện trên thẻ được rút ra là số chia cho 17 dư 2 và chia cho 3 dư 1”.
b) “Số xuất hiện trên thẻ được rút ra là số có chứa chữ số 5”.
Bài 24 :
Viết ngẫu nhiên một số tự nhiên có hai chữ số. Tính xác suất của mỗi biến cố sau:
a) “Số tự nhiên được viết ra là số chia hết cho cả 2 và 5”;
b) “Số tự nhiên được viết ra là số có tổng các chữ số bằng 5”.
Bài 25 :
Một đội thanh niên tình nguyện gồm 27 thành viên đến từ các tỉnh: Kom Tum, Gia Lai, Đắk Lắk, Đắk Nông, Lâm Đồng, Phú Yên, Khánh Hòa, Ninh Thuận, Bình Thuận, Bà Rịa – Vũng Tàu, Bình Dương, Bình Phước, Đồng Nai, Tây Ninh, Long An, Tiền Giang, Vĩnh Long, Bến Tre, Đồng Tháp, Trà Vinh, An Giang, Cần Thơ, Hậu Giang, Bạc Liêu, Sóc Trăng, Kiên Giang, Cà Mau; mỗi tỉnh chỉ có đúng một thành viên trong đội. Chọn ra ngẫu nhiên một thành viên của đội thanh niên trên. Tính xác suất của mỗi biến cố sau:
a) “Thành viên được chọn ra đến từ vùng Tây Nguyên”;
b) “Thành viên được chọn ra đến từ vùng Duyên hải miền Trung”;
c) “Thành viên được chọn ra đến từ vùng Đông Nam Bộ”;
d) “Thành viên được chọn ra đến từ vùng Đồng bằng sông Cửu Long”.
Bài 26 :
Xác suất của biến cố trong trò chơi có \(10\) kết quả có thể xảy ra là \(\frac{2}{5}\). Số kết quả thuận lợi của biến cố đó là
-
A.
5;
-
B.
2;
-
C.
4;
-
D.
6.
Bài 27 :
Một hộp có 48 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1; 2; …; 48. Hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là số chính phương”.
Bài 28 :
Xác suất của biến cố trong trò chơi gieo xúc xắc bằng
-
A.
Tích của số các kết quả thuận lợi cho biến cố và số các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc;
-
B.
Tỉ số của số các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc và số các kết quả thuận lợi cho biến cố;
-
C.
Hiệu của số các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc và số các kết quả thuận lợi cho biến cố;
-
D.
Tỉ số của số các kết quả thuận lợi cho biến cố và số các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc.
Bài 29 :
Vòng tứ kết cuộc thi bơi lội có sáu trường với 8 học sinh đại diện tham gia:
THCS Nguyễn Huệ: Kiệt;
THCS Nguyễn Khuyến: Long;
THCS Chu Văn An: Nguyên và Đăng;
THCS Nguyễn Bỉnh Khiêm: Minh;
THCS Lưu Văn Liệt: Thành;
THCS Nguyễn Du: Kha và Bình.
Xét biến cố “Người chiến thắng là học sinh đến từ trường THCS Nguyễn Huệ hoặc THCS Nguyễn Du”. Tính xác suất của biến cố trên.
-
A.
\(\frac{1}{4}\);
-
B.
\(\frac{3}{8}\);
-
C.
\(\frac{1}{3}\);
-
D.
\(\frac{1}{6}\).
Bài 30 :
Một nhóm du khách gồm 11 người đến từ các quốc gia: Anh; Pháp; Mỹ; Thái Lan; Bỉ; Ấn Độ; Hà Lan; Cu Ba; Nam Phi; Nhật Bản; Brasil. Chọn ngẫu nhiên một người trong nhóm du khách trên. Tính xác suất của biến cố “Du khách được chọn đến từ châu Âu”.




















Danh sách bình luận