Cho \(\Delta ABC\) vuông tại A, đường cao AH. Kẻ HE vuông góc với AB tại E và HF vuông góc với AC tại F.
a) Chứng minh tứ giác AFHE là hình chữ nhật.
b) Trên tia đối của tia FH lấy điểm M sao cho FH = FM. Trên tia đối của tia EH lấy điểm N sao cho EH = EN. Chứng minh tứ giác AEFM là hình bình hành.
c) Chứng minh A, M, N thẳng hàng.
a) Chứng minh tứ giác AFHE có 3 góc vuông nên là hình chữ nhật.
b) Chứng minh tứ giác AEFM có một cặp cạnh đối song song và bằng nhau nên là hình bình hành.
c) Chứng minh AN và AM cùng song song với EF.
Dựa vào tiên đề Euclid thì A, M, N thẳng hàng.
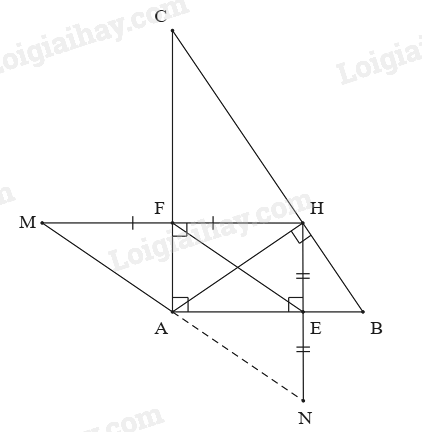
a) Xét tứ giác AFHE có:
\(\widehat A = \widehat E = \widehat F = 90^\circ \) (vì \(\Delta ABC\) vuông tại A, \(HE \bot AB\), \(HF \bot AC\))
Suy ra tứ giác AFHE là hình chữ nhật. (đpcm)
b) Vì FH // AE (do tứ giác AFHE là hình chữ nhật) nên MF // AE (vì F thuộc MH) (1)
Ta có FH = AE (do tứ giác AFHE là hình chữ nhật)
Mà FH = FM (giả thiết) suy ra AE = MF (2)
Từ (1) và (2) suy ra tứ giác AEFM là hình bình hành. (đpcm)
c) Vì AF = EH (do tứ giác AFHE là hình chữ nhật) nên AF // NE (vì E thuộc NH) (3)
Ta có AF = EH (do tứ giác AFHE là hình chữ nhật)
Mà HE = EN (gt) nên AF = NE (4)
Từ (3) và (4) suy ra tứ giác AFEN là hình bình hành.
Do đó AN // EF.
Mặt khác, AM // EF (vì tứ giác AEFM là hình bình hành)
Theo tiên đề Euclid thì A, M, N thẳng hàng. (đpcm)

Các bài tập cùng chuyên đề
Bài 1 :
Chọn câu sai. Tứ giác nào có hai đường chéo bằng nhau.
-
A.
Hình vuông
-
B.
Hình thang cân
-
C.
Hình chữ nhật
-
D.
Hình thoi
Bài 2 :
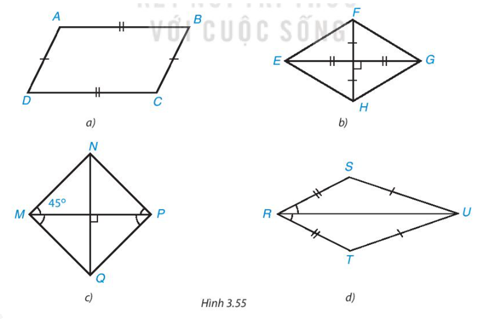
Tìm hình thoi và hình vuông trong Hình 3.55.
Bài 3 :
Cho tam giác ABC, D là một điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB, AC, chúng cắt các cạnh AC, AB lần lượt tại E, F.
a) Tứ giác AEDF là hình gì? Vì sao?
b) Nếu tam giác ABC cân tại A thì điểm D ở vị trí nào trên cạnh BC để tứ giác AEDF là hình thoi?
c) Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì?
d) Nếu tam giác ABC vuông cân tại A thì điểm D ở vị trí nào trên cạnh BC để AEDF là hình vuông?
Bài 4 :
Chứng minh rằng các trung điểm của bốn cạnh trong một hình chữ nhật là các đỉnh của một hình thoi.
Bài 5 :
Chứng minh rằng các trung điểm của bốn cạnh trong một hình thoi là các đỉnh của một hình chữ nhật.
Bài 6 :
Cho tam giác ABC; M và N lần lượt là trung điểm của hai cạnh AB và AC. Lấy điểm P sao cho N là trung điểm của đoạn thẳng MP.
a) Hỏi tứ giác AMCP là hình gì? Vì sao?
b) Với điều kiện nào của tam giác ABC thì tứ giác AMCP là hình chữ nhật; hình thoi; hình vuông?
Bài 7 :
Cho hình bình hành ABCD. Các tia phân giác của góc A, B, C, D cắt nhau như trên Hình 3.58. Chứng minh rằng EFGH là hình chữ nhật.
Bài 8 :
Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai?
a) Tứ giác có hai đường chéo bằng nhau là hình bình hành.
b) Tứ giác có hai cặp cạnh bằng nhau là hình bình hành.
c) Tứ giác có ba góc vuông là hình chữ nhật.
d) Tứ giác có ba cạnh bằng nhau là hình thoi.
Bài 9 :
Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai?
a) Tứ giác có hai đường chéo bằng nhau và hai cạnh đối nào cũng bằng nhau là hình chữ nhật.
b) Tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành.
c) Tứ giác có hai cạnh song song và hai đường chéo bằng nhau là hình thang cân.
d) Tứ giác có hai cạnh song song và hai cạnh còn lại bằng nhau là hình bình hành.
Bài 10 :
Cho hình bình hành ABCD. Lấy điểm P trên tia AB sao cho AP = 2 AB.
a) Tứ giác BPCD có phải là hình bình hành không? Tại sao?
b) Khi tam giác ABD vuông cân tại A, hãy tính số đo các góc của tứ giác BPCD.
Bài 11 :
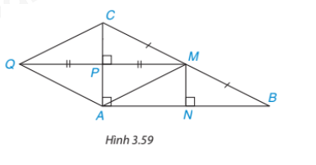
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC còn P, N lần lượt là chân đường vuông góc hạ từ M xuống CA, AB (H.3.59)
a) Chứng minh hai tam giác vuông CMP và MBN bằng nhau
b) Chứng minh tứ giác APMN là một hình chữ nhật. Từ đó suy ra N là trung điểm của AB, P là trung điểm của AC
c) Lấy điểm Q sao cho P là trung điểm của MQ, chứng minh rằng tứ giác AMCQ là một hình thoi
d) Nếu AB = AC, tức là tam giác ABC vuông cân tại A thì tứ giác AMCQ có là hình vuông không? Vì sao?
Bài 12 :
Cho hình bình hành \(ABCD\). Gọi \(I\) và \(K\) lần lượt là trung điểm của các cạnh \(AB\) và \(CD\); \(E\) và \(F\) lần lượt là giao điểm của \(AK\) và \(CI\) với \(BD\).
a) Chứng minh tứ giác \(AEFI\) là hình thang
b) Chứng minh \(DE = EF = FB\)
Bài 13 :
Tìm các hình bình hành và hình thang có trong hình 22.

Bài 14 :
Cho hình thoi \(ABCD\). Hãy chứng tỏ:
a) Nếu \(\widehat {BAD}\) là góc vuông thì ba góc còn lại của hình thoi cũng là góc vuông.
b) Nếu \(AC = BD\) thì \(\widehat {BAD}\) là góc vuông
Bài 15 :
Cho tam giác \(ABC\) vuông tại \(A\) (\(AB < AC\). Gọi \(D\) là trung điểm của \(BC\). Vẽ \(DE\) // \(AB\), vẽ \(DF\) // \(AC\) \((E \in AC\); \(F \in AB)\). Chứng minh rằng:
a) Tứ giác \(AEDF\) là hình chữ nhật
b) Tứ giác \(BFED\) là hình bình hành
Bài 16 :
Trong các khẳng định sau, khẳng định nào sai?
A. Tứ giác có ba góc vuông là hình chữ nhật
B. Hình bình hành có một góc vông là hình chữ nhật
C. Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình chữ nhật.
D. Tứ giác có các cạnh đối bằng nhau là hình bình hành
Bài 17 :
Cho tam giác \(ABC\) cân tại \(A\). Gọi \(H\), \(D\) lần lượt là trung điểm của các cạnh \(BC\) và \(AB\)
a) Chứng minh rằng tứ giác \(ADHC\) là hình thang
b) Gọi \(E\) là điểm đối xứng với \(H\) qua \(D\). Chứng minh rằng tứ giác \(AHBE\) là hình chữ nhật
c) Tia \(CD\) cắt \(AH\) tại \(M\) và cắt \(BE\) tại \(N\). Chứng minh rằng tứ giác \(AMBN\) là hình bình hành.
Bài 18 :
Cho tam giác \(ABC\) vuông tại \(A\) (\(AB < AC\)). Gọi \(M\), \(N\), \(E\) lần lượt là trung điểm của \(AB\), \(AC\), \(BC\)
a) Chứng minh rằng tứ giác \(ANEB\) là hình thang vuông
b) Chứng minh rằng tứ giác \(ANEM\) là hình chữ nhật
c) Qua \(M\) kẻ đường thẳng song song với \(BN\) cắt \(EN\) tại \(F\). Chứng minh rằng tứ giác \(AFCE\) là hình thoi
d) Gọi \(D\) là điểm đối cứng của \(E\) qua \(M\). Chứng minh rằng \(A\) là trung điểm của \(DF\)
Bài 19 :
Cho hình bình hành \(ABCD\) có \(AB = 2AD\). Gọi \(E\) và \(F\) lần lượt là trung điểm của \(DF\) và \(CD\), \(I\) là giao điểm của \(AF\) và \(DE\), \(K\) là giao điểm của \(BF\) và \(CE\)
a) Chứng minh rằng tứ giác \(AECF\) là hình bình hành
b) Tứ giác \(AEFD\) là hình gì? Vì sao?
c) Chứng minh tứ giác \(EIFK\) là hình chữ nhật
d) Tìm điều kiện của hình bình hành \(ABCD\) để tứ giác \(EIFK\) là hình vuông
Bài 20 :
Cho hình hình hành \(ABCD\) có \(AD = 2AB\). Từ \(C\) vẽ \(CE\) vuông góc với \(AB\) tại \(E\). Nối \(E\) với trung điểm \(M\) của \(AD\). Từ \(M\) vẽ \(MF\) vuông góc với \(CE\) tại \(F\), \(MF\) cắt \(BC\) tại \(N\).
a) Tứ giác \(MNCD\) là hình gì?
b) Chứng minh tam giác \(EMC\) cân tại \(M\)
c) Chứng minh rằng \(\widehat {BAD} = 2\widehat {AEM}\)
Hướng dẫn:
a) Chứng minh \(EN = NC = NB = \) \(\frac{1}{2}\) \(BC\)
b) Chứng minh \(\widehat {AEM} = \widehat {EMN} = \widehat {NMC} = \widehat {MCD} = \frac{1}{2}\widehat {NCD}\)
Bài 21 :
Cho bình bình hành ABCD. Gọi M là điểm nằm giữa A và B, N là điểm nằm giữa C và D sao cho AM = CN. Gọi I là giao điểm của MN và AC. Chứng minh:
a) \(\Delta IAM = \Delta ICN\)
b) Tứ giác AMCN là hình bình hành.
c) Ba điểm B, I, D thẳng hàng.
Bài 22 :
Cho hình thoi ABCD và hình bình hành BCMD. Gọi O là giao điểm của AC và BD. Chứng minh:
a) \(O{\rm{D}} = \frac{1}{2}CM\) và tam giác ACM là tam giác vuông.
b) Ba điểm A, D, M thẳng hàng.
c) Tam giác DCM là tam giác cân
Bài 23 :
Cho hình vuông ABCD có M, N lần lượt là trung điểm của các cạnh BC, CD. Gọi O là giao điểm của AM và BN. Chứng minh:
a) \(\Delta ABM = \Delta BCN\)
b) \(\widehat {BAO} = \widehat {MBO}\)
c) \(AM \bot BN\)
Bài 24 :
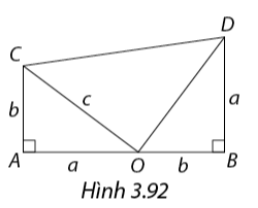
Tổng thống thứ 20 của Hợp chúng quốc Hoa Kỳ, James Abram Garfield đã đưa ra một cách chứng minh định lí Pythagore khá thú vị thông qua bài toán sau đây:
Cho Hình 3.92, trong đó \(ABCD\) là hình thang.
a) Chứng minh \(\Delta AOC = \Delta BDO\) và tam giác \(COD\) vuông cân.
b) Tính diện tích hình thang \(ABDC\) theo hai cách.
Từ đó suy ra \({c^2} = {a^2} + {b^2}\)
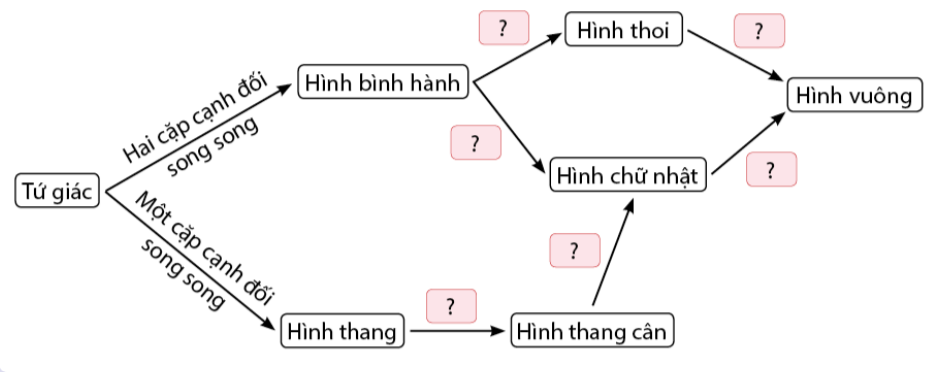
Bài 25 :
Tìm thông tin thích hợp cho các ô ? theo các mũi tên trong sơ đồ dưới đây:
Bài 26 :
Khẳng định nào sau đây đúng?
a) Hình thoi vừa là hình bình hành, vừa là hình thang cân;
b) Hình chữ nhật vừa là hình bình hành, vừa là hình thang cân;
c) Hình bình hành có một góc vuông là hình vuông.
Bài 27 :
Khẳng định nào sau đây đúng?
a) Nếu tứ giác có bốn cạnh bằng nhau thì các cặp cạnh đối của nó song song;
b) Tứ giác có hai đường chéo vuông góc và cắt nhau tại trung điểm mỗi đường là hình vuông;
c) Tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường là hình thoi;
d) Tứ giác có hai đường chéo bằng nhau là hình thang cân.
Bài 28 :
Cho biết các tứ giác trong Hình 3.93 là hình nào trong các hình: hình thang, hình thang cân, hình bình hành, hình thoi, hình chữ nhật, hình vuông. Vì sao?

Bài 29 :
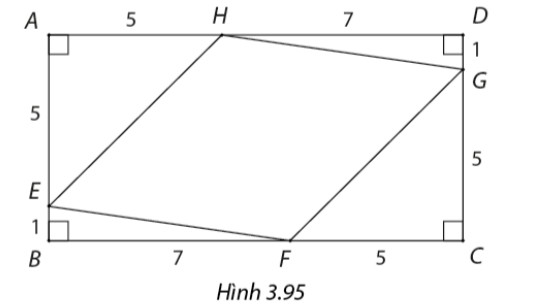
Trong Hình 3.95, \(ABCD\) là hình chữ nhật, \(E,F,G,H\) lần lượt là các điểm nằm trên các cạnh \(AB,BC,CD,AD\) và \(BE = DG = 1cm,BF = DH = 7cm,AE = AH = CF = CG = 5cm\).
a) Tính độ dài các cạnh của tứ giác \(EFGH\).
b) Chứng minh rằng \(HF\) vuông góc với \(EG\).
Bài 30 :
Chứng minh rằng:
a) Trong một hình bình hành (không là hình thoi), các tia phân giác của các góc cắt nhau tạo thành một hình chữ nhật.
b) Trong một hình chữ nhật (không là hình vuông), các tia phân giác của các góc cắt nhau tạo thành một hình vuông.



















Danh sách bình luận