Cho tam giác ABC có AC = b = 7, AB = c = 5, \(\cos A = \frac{3}{5}\).
a) Góc A là góc tù.
b) \(\sin A = - \frac{4}{5}\).
c) \(a = 4\sqrt 2 \).
d) Độ dài đường cao hạ từ đỉnh A bằng \(\frac{{7\sqrt 2 }}{2}\).
a) Góc A là góc tù.
b) \(\sin A = - \frac{4}{5}\).
c) \(a = 4\sqrt 2 \).
d) Độ dài đường cao hạ từ đỉnh A bằng \(\frac{{7\sqrt 2 }}{2}\).
a) Dựa vào giá trị lượng giác của một góc.
b) Sử dụng công thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\).
c) Sử dụng định lý Cosin trong tam giác.
d) Sử dụng công thức tính diện tích \(S = \frac{1}{2}bc\sin A = \frac{1}{2}{h_a}.a\).
a) Sai. Vì \(\cos A = \frac{3}{5} > 0\) và \({0^o} < A < {180^o}\) nên \(\widehat A\) là góc nhọn.
b) Sai. Ta có \({\sin ^2}A = 1 - {\cos ^2}A = 1 - {\left( {\frac{3}{5}} \right)^2} = \frac{{16}}{{25}}\), khi đó \(\sin A = \pm \frac{4}{5}\).
Vì \(\widehat A\) là góc nhọn nên \(\sin A > 0\), suy ra \(\sin A = \frac{4}{5}\).
c) Đúng. Ta có \({a^2} = {b^2} + {c^2} - 2bc\cos A = {5^2} + {7^2} - 2.5.7.\frac{3}{5} = 32\), suy ra \(a = 4\sqrt 2 \).
d) Đúng. Gọi \({h_a}\) là đường cao ứng với cạnh a trong tam giác.
\(S = \frac{1}{2}bc\sin A = \frac{1}{2}.5.7.\frac{4}{5} = 14\).
Mà \(S = \frac{1}{2}{h_a}.a\) suy ra \({h_a} = \frac{{2S}}{a} = \frac{{2.14}}{{4\sqrt 2 }} = \frac{{7\sqrt 2 }}{2}\).

Các bài tập cùng chuyên đề
Bài 1 :
Cho tam giác ABC có a = 6, b = 5, c =8. Tính cos A, S,r.
Bài 2 :
Giải tam giác ABC và tính diện tích của tam giác đó, biết \(\widehat A = {15^o},\;\widehat B = {130^o},\;c = 6\).
Bài 3 :
Từ bãi biển Vũng Chùa, Quảng Bình, ta có thể ngắm được Đảo Yến. Hãy đề xuất một các xác định bề rộng của hòn đảo (theo chiều ta ngắm được).

Bài 4 :
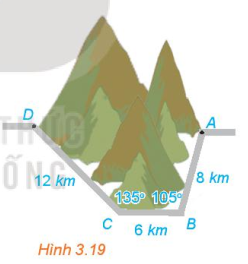
Để tránh núi, giao thông hiện tại phải đi vòng như mô hình trong Hình 3.19. Để rút ngắn khoảng cách và tránh sạt lở núi, người ta dự định làm đường hầm xuyên núi, nối thẳng từ A tới D. Hỏi độ dài đường mới sẽ giảm bao nhiêu kilômét so với đường cũ?
Bài 5 :
A. \({a^2} = {b^2} + {c^2} + \sqrt 2 ab.\)
B. \(\frac{b}{{\sin A}} = \frac{a}{{\sin B}}\)
C. \(\sin B = \frac{{ - \sqrt 2 }}{2}\)
D. \({b^2} = {c^2} + {a^2} - 2ca\cos {135^o}.\)
Bài 6 :
A. \(\sin A = \sin \,(B + C)\)
B. \(\cos A = \cos \,(B + C)\)
C. \(\;\cos A > 0\)
D. \(\sin A\,\, \le 0\)
Bài 7 :
A. \(S = \frac{{abc}}{{4r}}\)
B. \(r = \frac{{2S}}{{a + b + c}}\)
C. \({a^2} = {b^2} + {c^2} + 2bc\;\cos A\)
D. \(S = r\,(a + b + c)\)
Bài 8 :
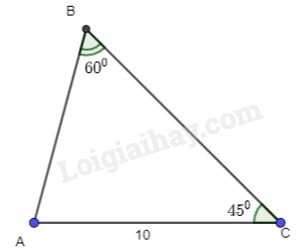
Cho tam giác ABC có \(\widehat B = {60^o},\;\,\widehat C = {45^o},AC = 10\). Tính \(a,R,S,r\).
Bài 9 :
Trên sân bóng chày dành cho nam, các vị trí gôn Nhà (Home plate), gôn 1 (First base), gôn 2 (Second base), gôn 3 (Third base) là bốn đỉnh của một hình vuông có cạnh dài 27,4 m. Vị trí đứng ném bóng (Pitcher’s mound) nằm trên đường nối gôn Nhà với gôn 2, và cách gôn Nhà 18,44 m. Tính các khoảng cách từ vị trí đứng ném bóng tới các gôn 1 và gôn 3.

Bài 10 :
Cho tam giác ABC có \(AB = 3,5;\;AC = 7,5;\;\widehat A = {135^o}.\) Tính độ dài cạnh BC và bán kính R của đường tròn ngoại tiếp tam giác (làm tròn kết quả đến hàng phần mười).
Bài 11 :
Cho tam giác ABC có \(AB = 6,AC = 7,BC = 8\). Tính \(\cos A,\sin A\) và bán kính R của đường trong ngoại tiếp tam giác ABC.
Bài 12 :
Tính giá trị đúng của các biểu thức sau (không dùng máy tính cầm tay):
a) \(A = \cos {0^o} + \cos {40^o} + \cos {120^o} + \cos {140^o}\)
b) \(B = \sin {5^o} + \sin {150^o} - \sin {175^o} + \sin {180^o}\)
c) \(C = \cos {15^o} + \cos {35^o} - \sin {75^o} - \sin {55^o}\)
d) \(D = \tan {25^o}.\tan {45^o}.\tan {115^o}\)
e) \(E = \cot {10^o}.\cot {30^o}.\cot {100^o}\)
Bài 13 :
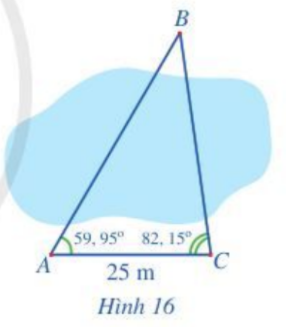
Để đo khoảng cách từ vị trí A đến vị trí B ở hai bên bờ một cái ao, bạn An đi dọc bờ ao từ vị trí A đến vị trí C và tiến hành đo các góc BAC, BCA. Biết AC = 25 m, \(\widehat {BAC} = 59,{95^o};\;\widehat {BCA} = 82,{15^o}.\) Hỏi khoảng cách từ vị trí A đến vị trí B là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
Bài 14 :
Hai tàu đánh cá cùng xuất phát từ bến A và đi thẳng đều về hai vùng biển khác nhau, theo hai hướng tạo với nhau góc \({75^o}\). Tàu thứ nhất chạy với tốc độ 8 hải lí một giờ và tàu thứ hai chạy với tốc độ 12 hải lí một giờ. Sau 2,5 giờ thì khoảng cách giữa hai tàu là bao nhiêu hải lí (làm tròn kết quả đến hàng phần mười)?
Bài 15 :
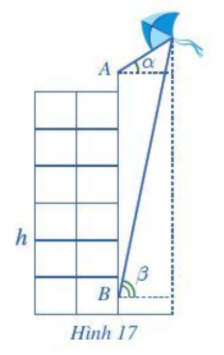
Bạn A đứng ở đỉnh của tòa nhà và quan sát chiếc diều, nhận thấy góc nâng (góc nghiêng giữa phương từ mắt của bạn A tới chiếc diều và phương nằm ngang) là \(\alpha = {35^o}\); khoảng cách từ đỉnh tòa nhà tới mắt bạn A là 1,5 m. Cùng lúc đó ở dưới chân tòa nhà, bạn B cũng quan sát chiếc diều và thấy góc nâng là \(\beta = {75^o}\); khoảng cách từ mặt đất đến mắt bạn B cũng là 1,5 m. Biết chiều cao của tòa nhà là h = 20 m (Hình 17). Chiếc diều bay cao bao nhiêu mét so mặt đất (làm tròn kết quả đến hàng đơn vị)?
Bài 16 :
Cho tam giác ABC có \(BC = 12,CA = 15,\widehat C = {120^o}.\) Tính:
a) Độ dài cạnh AB.
b) Số đo các góc A, B.
c) Diện tích tam giác ABC.
Bài 17 :
Cho tam giác ABC có \(AB = 5,BC = 7,\widehat A = {120^o}.\) Tính độ dài cạnh AC.
Bài 18 :
Cho tam giác ABC có \(AB = 100,\widehat B = {100^o},\widehat C = {45^o}.\) Tính:
a) Độ dài các cạnh AC, BC
b) Diện tích tam giác ABC.
Bài 19 :
Cho tam giác ABC có \(AB = 12,AC = 15,BC = 20.\) Tính:
a) Số đo các góc A, B, C.
b) Diện tích tam giác ABC.
Bài 20 :
Tính độ dài cạnh AB trong mỗi trường hợp sau:
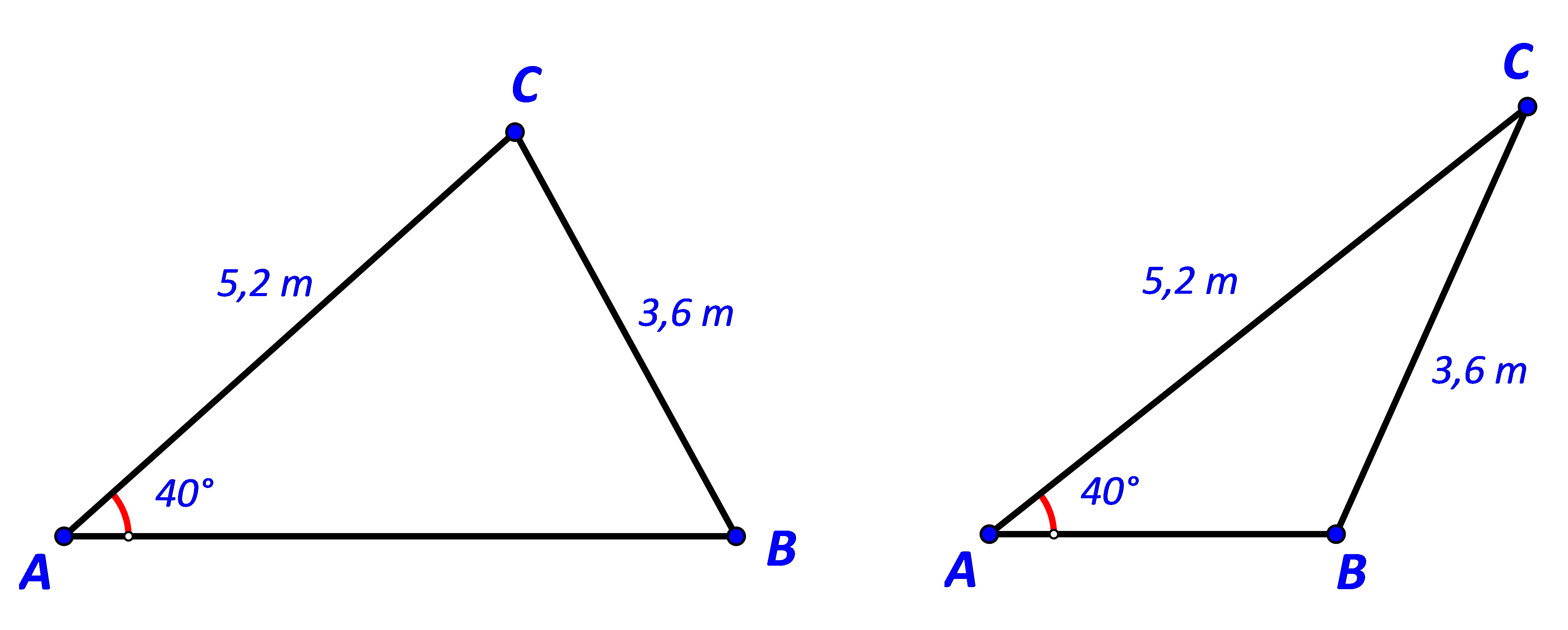
Bài 21 :
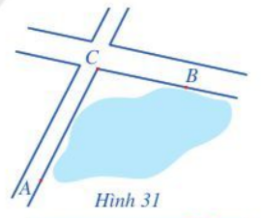
Để tính khoảng cách giữa hai địa điểm A và B mà ta không thể đi trực tiếp từ A đến B (hai địa điểm nằm ở hai bên bờ một hồ nước, một đầm lầy, …), người ta tiến hành như sau: Chọn một địa điểm C sao cho ta đo được các khoảng cách AC, CB và góc ACB. Sau khi đo, ta nhận được: AC = 1 km, CB = 800 m và \(\widehat {ACB} = {105^o}\) (Hình 31). Tính khoảng cách AB (làm tròn kết quả đến hàng phần mười đơn vị mét).
Bài 22 :
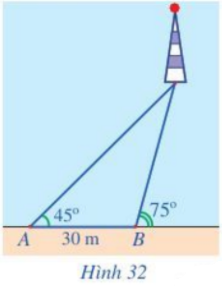
Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là \({45^o}\) và \({75^o}\). Biết khoảng cách giữa hai vị trí A, B là 30 m (Hình 32). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
Bài 23 :
Cho tam giác ABC có AB = 6, AC = 8 và \(\widehat A = {60^o}\).
a) Tính diện tích tam giác ABC.
b) Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Tính diện tích tam giác IBC.
Bài 24 :
Cho tam giác ABC có trọng tâm G và độ dài ba cạnh AB, BC, CA lần lượt là 15, 18, 27.
a) Tính diện tích và bán kính đường tròn nội tiếp tam giác ABC.
b) Tính diện tích tam giác GBC.
Bài 25 :
Cho tam giác ABC có góc B nhọn, AD và CE là hai đường cao.
a) Chứng minh \(\frac{{{S_{BDE}}}}{{{S_{BAC}}}} = \frac{{BD.BE}}{{BA.BC}}.\)
b) Biết rằng \({S_{ABC}} = 9{S_{BDE}}\) và \(DE = 2\sqrt 2 .\) Tính \(\cos B\) và bán kính đường tròn ngoại tiếp tam giác ABC.
Bài 26 :
Cho tứ giác lồi ABCD có các đường chéo \(AC = x,BD = y\) và góc giữa AC và BD bằng \(\alpha .\) Gọi S là diện tích của tứ giác ABCD.
a) Chứng minh \(S = \frac{1}{2}xy.\sin \alpha \)
b) Nêu kết quả trong trường hợp \(AC \bot BD.\)
Bài 27 :
b) Tính độ dài trung tuyến AM, diện tích tam giác và bán kính đường tròn ngoại tiếp tam giác đó.
Bài 28 :
c) Bán kính đường tròn ngoại tiếp và đường cao AH của tam giác.
Bài 29 :
Cho hình bình hành ABCD
a) Chứng minh \(2\left( {A{B^2} + B{C^2}} \right) = A{C^2} + B{D^2}\)
b) Cho \(AB = 4,BC = 5,BD = 7.\) Tính AC.
Bài 30 :
Cho tam giác ABC có \(a = 15,b = 20,c = 25.\)
a) Tính diện tích tam giác ABC
b) Tính bán kính đường tròn ngoại tiếp tam giác ABC


















Danh sách bình luận