Đề bài

Cho lăng trụ đứng $ABC.A'B'C'$ có đáy là tam giác vuông cân đỉnh $A,AB = AC = a,AA' = a\sqrt 2 $. Diện tích mặt cầu ngoại tiếp tứ diện $CA'B'C'$ là:

• A. $\dfrac{{4\pi {a^2}}}{3}$                         
• B. $4\pi {a^2}$                             
• C. $12\pi {a^2}$                         
• D. $4\sqrt 3 \pi {a^2}$

Phương pháp giải

- Xác định tâm mặt cầu ngoại tiếp từ diện $A'BB'C$

- Tính bán kính mặt cầu ngoại tiếp tứ diện $A'BB'C$

- Diện tích mặt cầu: $S = 4\pi {R^2}$

Lời giải của GV Loigiaihay.com

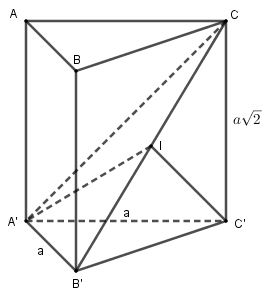
Ta có:

\(\begin{array}{l}A'B' = AB = a\\B'C' = \sqrt {A'B{'^2} + A'C{'^2}}  = \sqrt {{a^2} + {a^2}}  = a\sqrt 2 \\B'C = \sqrt {B'C{'^2} + C'{C^2}}  = \sqrt {2{a^2} + 2{a^2}}  = 2a\\A'C = \sqrt {A'C{'^2} + C'{C^2}}  = \sqrt {{a^2} + 2{a^2}}  = a\sqrt 3 \\ \Rightarrow A'B{'^2} + A'{C^2} = {a^2} + 3{a^2} = 4{a^2} = B'{C^2}\end{array}\)

\( \Rightarrow \Delta A'B'C\) vuông tại \(A'\).

Gọi \(I\) là trung điểm của \(B'C\) thì \(IB' = IC = IA'\)

Mà \(\Delta CC'B'\) vuông tại \(C'\) nên \(IB' = IC = IC'\)

Vậy \(I\) là tâm mặt cầu ngoại tiếp tứ diện \(CA'B'C'\) và bán kính \(R = \frac{1}{2}B'C = a\).

\( \Rightarrow S = 4\pi {R^2} = 4\pi {a^2}\).

Đáp án : B