Vẽ đồ thị của các hàm số sau:
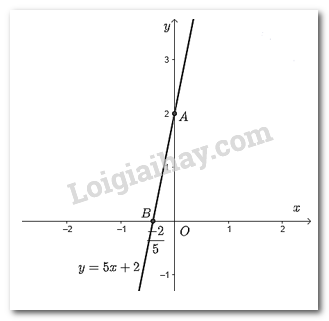
a) \(y = 5x + 2\);
b) \(y = - 2x - 6\);
Để vẽ đồ thị hàm số \(y = ax + b\) ta làm như sau:
Bước 1: Cho \(x = 0 \Rightarrow y = b\) ta được điểm \(M\left( {0;b} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - b}}{a}\) ta được điểm \(N\left( {\dfrac{{ - b}}{a};0} \right)\) trên \(Ox\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(M\) và \(N\), ta được đồ thị của hàm số \(y = ax + b\).
a) \(y = 5x + 2\);
Cho \(x = 0 \Rightarrow y = 2\) ta được điểm \(A\left( {0;2} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 2}}{5}\) ta được điểm \(B\left( {\dfrac{{ - 2}}{5};0} \right)\) trên \(Ox\).
Vẽ đường thẳng đi qua hai điểm \(A;B\) ta được đồ thị của hàm số \(y = 5x + 2\).
b) \(y = - 2x - 6\)
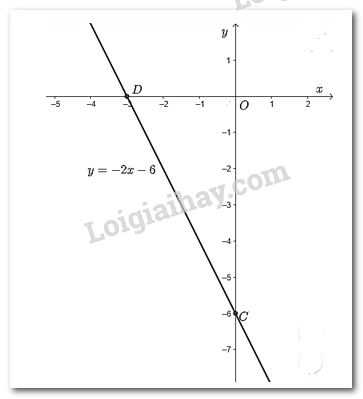
Cho \(x = 0 \Rightarrow y = - 6\) ta được điểm \(C\left( {0; - 6} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = - 3\) ta được điểm \(D\left( { - 3;0} \right)\) trên \(Ox\).
Vẽ đường thẳng đi qua hai điểm \(C;D\) ta được đồ thị của hàm số \(y = - 2x - 6\).
Các bài tập cùng chuyên đề
Đồ thị hàm số bậc nhất \(y = {\rm{ax + b}}\left( {a \ne 0} \right)\)có tính chất gì?
Vẽ đồ thị của mỗi hàm số sau:
a) y = 3x
b) y = 2x + 2
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai về hai đường thẳng d là đồ thị của hàm số y = ax + b \(\left( {a \ne 0} \right)\)?
a) Đường thẳng d cắt trục hoành tại điểm có hoành độ bằng \( - \dfrac{b}{a}\).
b) Đường thẳng d cắt trục tung tại điểm có tung độ bằng \( - \dfrac{b}{a}\)
c) Đường thẳng d cắt trục hoành tại điểm có hoành độ bằng b.
d) Đường thẳng d cắt trục tung tại điểm có tung độ bằng b.
Vẽ đồ thị các hàm số \(y = 3{\rm{x}};y = 3{\rm{x}} + 4;y = - \dfrac{1}{2}x;y = - \dfrac{1}{2}x + 3\) trên cùng một mặt phẳng tọa độ.
a) Vẽ đường thẳng y = 2x -1 trên mặt phẳng tọa độ
b) Xác định đường thẳng y = ax + b \(\left( {a \ne 0} \right)\) đi qua điểm M (1; 3) và song song với đường thẳng y = 2x -1. Sau đó vẽ đường thẳng tìm được trên mặt phẳng tọa độ.
Cho hai hàm số: \(y = - \dfrac{1}{2}x + 3;y = 2{\rm{x}} - 2\)
a) Vẽ đồ thị của hai hàm số đó trên cùng một mặt phẳng tọa độ.
b) Gọi A, B lần lượt là giao điểm của hai đường thẳng \(y = - \dfrac{1}{2}x + 3;y = 2{\rm{x}} - 2\) với trục hoành và C là giao điểm của hai đường thẳng đó. Tính diện tích của tam giác ABC (đơn vị đo trên các trục là centimét)
a) Biết rằng với x = 3 thì hàm số y = 2x + b có giá trị là 11. Tìm b và vẽ đồ thị của hàm số với giá trị b vừa tìm được.
b) Biết rằng đồ thị của hàm số y = ax + 6 đi qua điểm A (-2; 2). Tìm a và vẽ đồ thị hàm số với giá trị a vừa tìm được.
Trong các phát biểu sau, phát biểu nào đúng?
a) Để vẽ đồ thị của hàm số \(y = ax + b\left( {a \ne 0,b \ne 0} \right)\), ta có thể xác định hai điểm \(P\left( {0;b} \right)\) và \(Q\left( { - \frac{b}{a};0} \right)\) rồi vẽ đường thẳng đi qua hai điểm đó.
b) Để vẽ đồ thị của hàm số \(y = ax + b\left( {a \ne 0,b \ne 0} \right)\), ta có thể xác định hai điểm \(M\left( { - 1; - a + b} \right)\) và \(N\left( { - \frac{b}{a};b} \right)\) rồi vẽ đường thẳng đi qua hai điểm đó.
c) Để vẽ đồ thị của hàm số \(y = ax + b\left( {a \ne 0,b \ne 0} \right)\), ta có thể xác định hai điểm \(I\left( {1;a + b} \right)\) và \(K\left( { - 2; - 2a + b} \right)\) rồi vẽ đường thẳng đi qua hai điểm đó.
Vẽ đồ thị của các hàm số \(y = - x,y = - x - 1,y = - \frac{1}{3}x,y = \frac{1}{3}x + 2\) trên cùng một mặt phẳng tọa độ.
A. \(\left( {0; - 1} \right)\)
B. \(\left( { - \frac{7}{3};2} \right)\)
C. \(\left( {0;\frac{1}{4}} \right)\)
D. \(\left( {3; - 2} \right)\)
Trong mặt phẳng tọa độ \(Oxy\), cho các điểm \(A\left( {2;3} \right),B\left( {2; - 4} \right)\). Tìm tọa độ điểm \(C\) sao cho \(C\) nằm trên trục \(Ox\) và \(CA + CB\) đạt giá trị nhỏ nhất.
Cho hai hàm số \(y = x + 5;y = - x + 1\).
a) Vẽ đồ thị của hai hàm số đó trên cùng một mặt phẳng tọa độ.
b) Gọi \(A\) là giao điểm của hai đường thẳng \(y = x + 5;y = - x + 1\); \(B,C\) lần lượt là giao điểm của hai đường thẳng đó với trục \(Ox\). Tính diện tích của tam giác \(ABC\) (đơn vị đo trên các trục tọa độ là centimet).
Vẽ đồ thị của các hàm số y=−2x+3 và \(y = \frac{1}{2}x\)
Vẽ đồ thị của các hàm số sau
a) y = 2x − 6
b) y = −3x + 5
c) \(y = \frac{3}{2}x\)
Cho hai hàm số y=2x−1 và y=−x+2
a) Trong cùng mặt phẳng tọa độ Oxy, vẽ đồ thị của hai hàm số đã cho
b) Tìm tọa độ giao điểm của hai đồ thị trên
Cho hàm số bậc nhất y=(3−m)x+2m+1
Tìm các giá trị của m để đồ thị của hàm số đã cho là:
a) Đường thẳng đi qua điểm (1;2)
b) Đường thẳng cắt đường thẳng y=x+1 tại một điểm nằm trên trục tung
Hùng mua \(x\) mét dây điện và phải trả số tiền là \(y\) nghìn đồng. Giá trị tương ứng giữa \(x\)và \(y\) được cho bởi bảng sau:
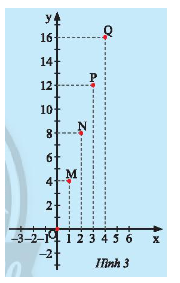
Hùng vẽ các điểm \(M\left( {1;4} \right);N\left( {2;8} \right);P\left( {3;12} \right);Q\left( {4;16} \right)\) trên mặt phẳng tọa độ \(Oxy\) như Hình 3. Hãy dùng thước thẳng để kiểm tra các điểm \(O;M;N;P;Q\) có thẳng hàng không.
a) Vẽ đồ thị của hàm số: \(y = 0,5x;y = - 3x;y = x\).
b) Các đồ thị sau đây là đồ thị của hàm số nào?
Cho hàm số \(y = f\left( x \right) = x\) và \(y = g\left( x \right) = x + 3\)
a) Thay dấu ? bằng số thích hợp.
b) Trên cùng một mặt phẳng tọa độ, vẽ đồ thị của hàm số \(y = f\left( x \right)\) và biểu diễn các điểm có tọa độ thỏa mãn hàm số \(y = g\left( x \right)\) có trong bảng trên.
c) Kiểm tra xem các điểm thuộc đồ thị hàm số của \(y = g\left( x \right)\) vẽ ở câu b có thẳng hàng không. Và dự đoán cách vẽ đồ thị hàm số \(y = g\left( x \right)\).
Một lò xo có chiều dài ban đầu khi chưa treo vật nặng là 10 cm. Cho biết treo thêm vào lò xo 1 vật nặng 1 kg thì chiều dài lò xo tăng thêm 3 cm.
a) Tính chiều dài \(y\) (cm) của lò xo theo khối lượng \(x\) (kg) của vật.
b) Vẽ đồ thị của hàm số \(y\) theo biến số \(x\).
Vẽ đồ thị các hàm số sau đây trên cùng một mặt phẳng tọa độ:
\(y = x\);
\(y = x + 2\);
\(y = - x\);
\(y = - x + 2\).
Một người đi bộ trên đường thẳng với tốc độ \(v\left( {km/h} \right)\). Gọi \(s\left( {km} \right)\) là quãng đường đi được trong \(t\left( h \right)\).
Vẽ đồ thị của hàm số \(s\) theo \(t\) khi \(v = 4\).
Lam phụ giúp mẹ bánh nước chanh, em nhận thấy số ly nước chanh \(y\) bán được trong ngày và nhiệt độ trung bình \(x\left( {^\circ C} \right)\) của ngày hôm đó có mối tương quan. Lan ghi lại các giá trị tương ứng của hai đại lượng \(x\) và \(y\) trong bảng sau:
So sánh các giá trị \(x\) và \(y\) tương ứng trong bảng dữ liệu trên với tọa độ \(\left( {x;y} \right)\) của các điểm \(A;B;C;D;E;F\) trên mặt phẳng tọa độ trong Hình 6.
Một người bắt đầu mở một vòi nước vào một cái bể đã chứa sẵn 3 \({m^3}\) nước, mỗi giờ chảy được 1 \({m^3}\).
Vẽ đồ thị của hàm số \(y\) theo biến số \(x\).
Đồ thị hàm số \(y = \dfrac{{ - x + 10}}{5}\)
A. là một đường thẳng có hệ số góc là -1.
B. không phải là một đường thẳng.
C. cắt trục hoành tại điểm có hoành độ là 10.
D. đi qua điểm \(\left( {200;50} \right)\).
Cho biết đồ thị của hàm số \(y = ax\) đi qua điểm \(P\left( {1; - \dfrac{4}{5}} \right)\). Vẽ điểm trên đồ thị có hoành độ bằng \( - 5\).
Cho biết đồ thị của hàm số \(y = ax\) đi qua điểm \(P\left( {1; - \dfrac{4}{5}} \right)\). Vẽ điểm trên đồ thị có tung độ bằng 2.
Một người đi bộ với tốc độ không đổi 3\(km/h\). Gọi \(s\left( {km} \right)\) là quãng đường đi được trong \(t\) (giờ).
a) Lập công thức tính \(s\) theo \(t\).
b) Vẽ đồ thị của hàm số \(s\) theo biến số \(t\).
Cho hai hàm số \(y = x + 3\), \(y = - x + 3\) có đồ thị lần lượt là các đường thẳng \({d_1}\) và \({d_2}\). Bằng cách vẽ hình, tìm tọa độ giao điểm \(A\) của hai đường thẳng nói trên và tìm các giao điểm \(B,C\) lần lượt của \({d_1}\) và \({d_2}\) với trục \(Ox\).
Hình 5.23 biểu diễn các điểm \(O\left( {0;0} \right),A\left( {1;3} \right),B\left( {2;6} \right)\) và \(O'\left( {0; - 2} \right),A'\left( {1;1} \right),B'\left( {2;4} \right)\) trên mặt phẳng tọa độ.
a) Nhận xét về sự song song giữa \(OA\) và \(O'A'\); \(AB\) và \(A'B'\).
b) Đồ thị hàm số \(y = 3x\) có đi qua các điểm \(O,A,B\) không?
c) Đồ thị hàm số \(y = 3x - 2\) có đi qua các điểm \(O',A',B'\) không?
