Cho hai tập hợp \(A = \left\{ {\left( {x;y} \right)\left| {3x - 2y = 11} \right.} \right\},B = \left\{ {\left( {x;y} \right)\left| {2x + 3y = 3} \right.} \right\}\). Hãy xác định tập hợp \(A \cap B\).
Bước 1: Đưa tập hợp về dạng cùng x (hoặc y), biểu diễn y (hoặc x) qua biến còn lại.
Bước 2: Giải phương trình để các phần tử của hai tập hợp giống nhau.
Ta có biểu diễn các tập hợp như sau:
\(A = \left\{ {\left( {x;y} \right)\left| {x = \frac{{11 + 2y}}{3}} \right.} \right\},B = \left\{ {\left( {x;y} \right)\left| {x = \frac{{3 - 3y}}{2}} \right.} \right\}\)
Tập hợp \(A \cap B\) là tập hợp các phần tử vừa thuộc tập hợp A vừa thuộc tập hợp B, suy ra \(\frac{{11 + 2y}}{3} = \frac{{3 - 3y}}{2}\)
Giải phương trình trên ta có: \(\frac{{11 + 2y}}{3} = \frac{{3 - 3y}}{2} \Leftrightarrow y = - 1 \Rightarrow x = 3\)
Suy ra \(A \cap B = \left\{ {\left( {3; - 1} \right)} \right\}\).
Các bài tập cùng chuyên đề
Cho các tập hợp C = [1; 5], D = [-2; 3]. Hãy xác định tập hợp \(C \cap \;D\).
Viết tập hợp X gồm những thành viên tham gia cả hai chuyên đề 1 và 2 trong tình huống mở đầu.
Tập X có phải là tập con của tập A không? Tập X có phải là tập con của tập B không? (A, B là các tập hợp trong HĐ1).
Cho tập hợp A,B được mình họa bằng biểu đồ Ven như hình bên. Phần tô màu xám trong hình là biểu diễn của tập hợp nào sau đây?
A. \(A \cap B\)
B. \(A\;{\rm{\backslash }}\;B\)
C. \(A \cup B\)
D. \(B\;{\rm{\backslash }}\;A\)
Hoạt động 6 trang 7 Sách giáo khoa Toán 10 tập 1 – Cánh diều
Lớp trưởng lập hai danh sách các bạn đăng kí tham gia câu lạc bộ thể thao như sau (biết trong lớp không có hai bạn nào cùng tên):
- Bóng đá gồm: An, Bình, Chung, Dũng, Minh, Nam, Phương.
- Bóng rổ gồm: An, Chung, Khang, Phong, Quang, Tuấn.
Hãy liệt kê danh sách các bạn đăng kí tham gia cả hai câu lạc bộ.
Cho \(A = \{ (x;y)|x,y \in \mathbb{R},3x - y = 9\} \), \(B = \{ (x;y)|\;x,y \in \mathbb{R},x - y = 1\} \)
Hãy xác định \(A \cap B\).
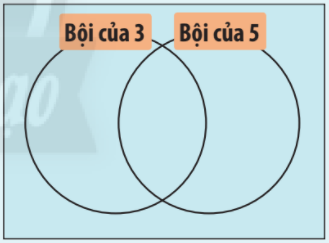
Có 2 đường tròn chia một hình chữ nhật thành các miền như hình bên. Hãy đặt mooix thẻ số sau đây vào miền thích hợp trên hình chữ nhật và giải thích cách làm
|
65 |
75 |
78 |
82 |
90 |
|||
|
94 |
100 |
120 |
231 |
||||
Xác định các tập hợp \(A \cap B\) trong mỗi trường hợp sau:
a) \(A = \{ x \in \mathbb{R}|{x^2} - 2 = 0\} ,\)\(B = \{ x \in \mathbb{R}|2x - 1 < 0\} \)
b) \(A = \{ (x;y)|\;x,y \in \mathbb{R},y = 2x - 1\} ,\)\(B = \{ (x;y)|\;x,y \in \mathbb{R},y = - x + 5\} \)
c) A là tập hợp các hình thoi, B là tập hợp các hình chữ nhật.
Cho hai tập hợp \(A = \left[ {a;5} \right]\) và \(B = \left[ { - 2;3} \right],\) với \(a < 5.\) Số a cần thảo mãn điều kiện gì để \(A \cap B = \emptyset .\)
Cho hai tập hợp \(A = \left( { - 3;3} \right],B = \left( {2; + \infty } \right)\). Tập hợp \(A \cap B\)bằng:
A. \(\left\{ { - 1;0;1;2;3} \right\}\)
B. \(\left[ { - 2; - 3} \right]\)
C. \(\left( { - 2;3} \right]\)
D. \(\left( { - 3; + \infty } \right)\)
Tìm \(D = E \cap G\), biết E và G lần lượt là tập nghiệm của hai bất phương trình trong mỗi trường hợp sau:
a) \(5x - 2 > 0\)và \(3x + 7 \ge 0\)
b) \(2x + 3 > 0\)và \(5x - 9 \le 0\)
c) \(9 - 3x \ge 0\)và \(12 - 3x < 0\)
Cho \(A = \left[ {m;m + 2} \right]\)và \(B = \left[ {n;n + 1} \right]\) với m, n là các tham số thực. Tìm điều kiện của các số m và n để tập hợp \(A \cap B\)chứa đúng một phần tử.
