Trong các tập hợp sau, tập hợp nào rỗng?
A. \(M = \left\{ {x \in N|{x^2} - 16 = 0} \right\}.\)
B. \(N = \left\{ {x \in \mathbb{R}|{x^2} + 2x + 5 = 0} \right\}.\)
C. \(P = \left\{ {x \in \mathbb{R}|{x^2} - 15 = 0} \right\}.\)
D. \(Q = \left\{ {x \in \mathbb{Q}|{x^2} + 3x - 4 = 0} \right\}\)
- Giải các phương trình \({x^2} - 16 = 0,\,\,{x^2} + 2x + 5 = 0,\,\,{x^2} - 15 = 0,\,\,{x^2} + 3x - 4 = 0\)
- Dùng phương pháp loại trừ rồi kết luận
Xét phương trình: \({x^2} - 16 = 0\,\, \Leftrightarrow x = \pm 4\) (thỏa mãn)
\( \Rightarrow M = \left\{ { - 4;4} \right\}\)
Xét phương trình: \({x^2} + 2x + 5 = 0\,\, \Leftrightarrow \,\,{\left( {x + 1} \right)^2} + 4 = 0\) (vô lý)
\( \Rightarrow \,\,N = \emptyset .\)
Chọn B
Các bài tập cùng chuyên đề
Mô tả tập hợp \(A = \{ x \in \mathbb{Z}| - 1 \le x < 2\} \) bằng cách liệt kê:
Gọi S là tập nghiệm của phương trình \({x^2} - 24x + 143 = 0\).
Các mệnh đề sau đúng hay sai?
a) \(13 \in S\)
b) \(11 \notin S\)
c) \(n\;(S) = 2\)
Cho tập hợp:
C = {châu Á; châu Âu; châu Đại Dương; châu Mĩ; châu Nam Cực; châu Phi}.
a) Hãy chỉ ra tính chất đặc trưng cho các phần tử của tập hợp C.
b) Tập hợp C có bao nhiêu phần tử?
Gọi X là tập hợp các quốc gia tiếp giáp với Việt Nam. Hãy liệt kê các phần tử của tập hợp X và biểu diễn tập X bằng biểu đồ Ven.
Kí hiệu E là tập hợp các quốc gia tại khu vực Đông Nam Á.
a) Nếu ít nhất hai phần tử thuộc tập hợp E.
b) Nêu ít nhất hai phần tử không thuộc tập hợp E.
c) Liệt kê các phần tử thuộc tập hợp E. Tập hợp E có bao nhiêu phần tử?
Hãy viết tập hợp sau bằng cách nêu tính chất đặc trưng cho các phần tử của tập hợp: A = {0; 4; 8; 12; 16}
Trong các tập hợp sau, tập hợp nào là tập hợp rỗng?
\(A = \left\{ {x \in \mathbb{R}|\;{x^2} - 6 = 0} \right\}\);
\(B = \left\{ {x \in \mathbb{Z}|\;{x^2} - 6 = 0} \right\}\)
Nêu số phần tử của mỗi tập hợp sau:
\(G = \{ x \in \mathbb{Z}|{x^2} -2 = 0\} ,\) \(\mathbb{N}* = \left\{ {1;2;3;..} \right\}.\)
Nêu số phần tử của mỗi tập hợp sau:
\(C = \{ x \in \mathbb{R}|{x^2} < 0\} ,\) \(D = \{ a\} ,E = \{ b;c;d\} ,\)\(\mathbb{N} = \left\{ {0;1;2;..} \right\}\)
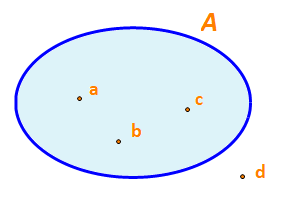
Người ta còn minh họa tập hợp bằng một vòng kín, mỗi phần tử của tập hợp được biểu diễn bởi một chấm bên trong vòng kín, còn phần tử không thuộc tập hợp đó được biểu diễn bởi một chấm bên ngoài vòng kín (Hình 1). Cách minh họa tập hợp như vậy được gọi là biểu đồ Ven.
a) Viết tập hợp A trong Hình 1 bằng cách liệt kê các phần tử của các tập hợp đó.
b) Nêu phần tử không thuộc tập hợp A
Gọi A là tập nghiệm của đa thức P(x). Viết tập hợp các số thực x sao cho biểu thức \(\dfrac{1}{{P(x)}}\) xác định.
Viết các tập hợp sau đây dưới dạng chỉ ra tính chất đặc trưng cho các phần tử:
a) \(A = \{ 1;3;5;...;15\} \)
b) \(B = \{ 0;5;10;.15;20;...\} \)
c) Tập hợp C các nghiệm của bất phương trình \(2x + 5 > 0.\)
Viết tập hợp sau đây dưới dạng liệt kê các phần tử và tìm số phần tử của mỗi tập hợp đó:
a) Tập hợp A các ước của 24
b) Tập hợp B gồm các chữ số trong số 1113305;
c) \(C = \{ n \in \mathbb{N}|\;n\) là bội của 5 và \(n \le 30\} \)
d) \(D = \{ x \in \mathbb{R}|\;{x^2} - 2x + 3 = 0\} \)
Viết các tập hợp sau đây dưới dạng liệt kê các phần tử:
a) \(A = \{ x \in \mathbb{Z}|\;|x|\; < 5\} \)
b) \(B = \{ x \in \mathbb{R}|\;2{x^2} - x - 1 = 0\} \)
c) \(C = \{ x \in \mathbb{N}\;|x\) có hai chữ số\(\} \)
Viết các tập hợp sau đây dưới dạng chỉ ra tính chất đặc trưng cho các phần tử:
a) Tập hợp \(A = \{1;2;3;6;9;18\} \)
b) Tập hợp \(B\) các nghiệm của bất phương trình \(2x+1>0\)
c) Tập hợp \(C\) các nghiệm của phương trình \(2x-y=6\)
Cho hai tập hợp \(A,\,\,B\) được mô tả bởi biểu đồ ven như sau:
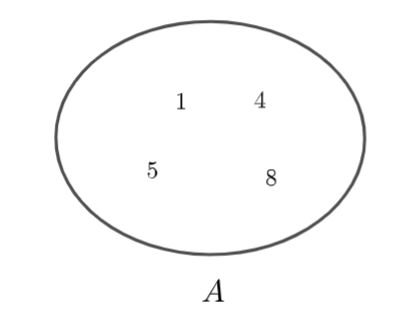
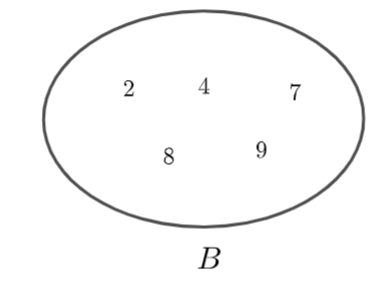
a) Hãy chỉ ra các phần tử của tập hợp \(A,\) tập hợp \(B.\)
b) Tính \(n\left( {A \cup B} \right)\)
c) Hãy chỉ ra các phần tử thuộc tập hợp \(A\) mà không thuộc tập hợp \(B.\)
d) Hãy chỉ ra các phần tử thuộc tập hợp \(B\) mà không thuộc tập hợp \(A.\)
Xác định các tập hợp sau bằng cách nêu tính chất đặc trưng cho các phần tử của tập hợp.
\(A = \left\{ {0;4;8;12;16} \right\},\quad B = \left\{ { - 3;9; - 27;81} \right\}\)
\(C\) là đường thẳng trung trực của đoạn thẳng \(AB.\)
Trong các tập hợp sau, tập hợp nào rỗng?
\(A = \left\{ {\left. {x \in \mathbb{N}} \right|x \le 0} \right\};\quad B = \left\{ {\left. {x \in \mathbb{N}} \right|2{x^2} - 3x - 5 = 0} \right\}\)
Xác định các tập hợp sau và biểu diễn chúng trên trục số.
a) \(\left( {4;7} \right) \cap \left( { - 1;3} \right)\)
b) \(\left( { - 2;1} \right] \cap \left( { - \infty ;1} \right)\)
c) \(( - 2; 6) \) \ \((3;10)\)
d) \((- 3;5)\) \ \([2;8)\)
Hãy viết các tập hợp sau bằng cách liệt kê các phần tử của tập hợp.
\(A = \left\{ {\left. {x \in \mathbb{Q}} \right|\left( {2x + 1} \right)\left( {{x^2} + x - 1} \right)\left( {2{x^2} - 3x + 1} \right) = 0} \right\};\)
\(B = \left\{ {\left. {x \in \mathbb{N}} \right|{x^2} > 2\,\, \rm{và} \,\,x < 4} \right\}\)
Cho hai tập hợp sau:
\(A = \left\{ {\left. {x \in \mathbb{R}} \right|\left| x \right| \le 4} \right\};\quad B = \left\{ {\left. {x \in \mathbb{R}} \right| - 3 < x \le 8} \right\}\)
a) Viết hai tập hợp trên dưới dạng khoảng, đoạn.
b) Xác định các tập hợp sau: \(A \cap B;\,\,A\backslash B;\,\,B\backslash A\).
Cho tập hợp \(A = \left\{ {x \in \mathbb{N}|x \le 4} \right\}\). A là tập hợp nào sau đây?
A. \(\left\{ {0;1;2;3;4} \right\}\)
B. \(\left( {0;4} \right]\)
C. \(\left\{ {0;4} \right\}\)
D. \(\left\{ {1;2;3;4} \right\}\)
Xác định các tập hợp sau
a) \(\left[ { - 2;3} \right] \cap \left( {0;5} \right)\)
b) \(\left( { - 3;1} \right] \cap \left( {1; + \infty } \right)\)
c) \(\left( { - \infty ;0} \right) \cup \left( { - 2;2} \right]\)
d) \(\left( { - \infty ;0} \right) \cup \left[ {0; + \infty } \right)\)
e) \(\mathbb{R}\backslash \left[ {1; + \infty } \right)\)
g) \(\left[ {3;5} \right]\backslash \left( {4;6} \right)\)
Cho tập hợp \(A = \left\{ {x \in \mathbb{R}\left| { - 3 \le x} \right. < 2} \right\}\). A là tập hợp nào sau đây?
A. \(\left( { - 3;2} \right)\)
B. \(\left\{ { - 3; - 2; - 1;0;1} \right\}\)
C. \(\left\{ { - 3;2} \right\}\)
D. \(\left[ { - 3;2} \right)\)
Cho hai tập hợp \(A = \left\{ {x \in \mathbb{R}\left| {x + 3} \right. < 4 + 2x} \right\},B = \left\{ {x \in \mathbb{R}\left| {5x - 3 < 4x - 1} \right.} \right\}\). Tất cả các số nguyên thuộc cả hai tập hợp A và B là:
A. 0 và 1
B. -1; 0; 1 và 2
C. 1 và 2
D. 1
Dùng kí hiệu để viết mỗi tập hợp sau và biểu diễn mỗi tập hợp đó trên trục số:
a) \(A = \left\{ {x \in \mathbb{R}\left| { - 7 < x < - 4} \right.} \right\}\)
b) \(B = \left\{ {x \in \mathbb{R}\left| { - 3 \le x \le - 1} \right.} \right\}\)
c) \(C = \left\{ {x \in \mathbb{R}\left| {x \le 0} \right.} \right\}\)
d) \(D = \left\{ {x \in \mathbb{R}\left| {x > - 1} \right.} \right\}\)
Viết các tập hợp sau dưới dạng liệt kê các phần tử.
a) \(A = \left\{ {x\left| {{x^2} - 2x - 15 = 0} \right.} \right\}\)
b) \(B = \left\{ {x \in \mathbb{Z}\left| { - 3 < x \le 2} \right.} \right\}\)
c) \(C = \left\{ {\frac{n}{{{n^2} - 1}}\left| {n \in \mathbb{N},1 < n \le 4} \right.} \right\}\)
d) \(D = \left\{ {\left( {x;y} \right)\left| {x \le 2,y < 2,x,y \in \mathbb{N}} \right.} \right\}\)
Viết các tập hợp sau đây bằng cách chỉ ra tính chất đặc trung của các phần tử:
a) \(A = \left\{ { - 4; - 3; - 2; - 1;0;1;2;3;4} \right\}\)
b) \(B = \left\{ {0;2;4;6;8;10} \right\}\)
c) \(C = \left\{ {1;\frac{1}{2};\frac{1}{3};\frac{1}{4};\frac{1}{5}} \right\}\)
d) Tập hợp D các số thực lớn hơn hoặc bằng 3 và bé hơn 8
Viết các tập hợp sau đây dưới dạng liệt kê các phần tử.
a) \(A = \left\{ {y \in \mathbb{N}\left| {y = 10 - {x^2},x \in \mathbb{N}} \right.} \right\}\)
b) \(B = \left\{ {x \in \mathbb{N}\left| {\frac{6}{{6 - x}} \in \mathbb{N}} \right.} \right\}\)
c) \(C = \{ x \in \mathbb{N}| 2x - 3 \ge 0 \) và \(7 - x \ge 2 \}\)
d) \(D = \left\{ {\left( {x;y} \right)\left| {x \in \mathbb{N},y \in \mathbb{N},x + 2y = 8} \right.} \right\}\)
Cho tập hợp \(M = \left\{ {x \in \mathbb{N}\left| {x = 5 - m,m \in \mathbb{N}} \right.} \right\}\). Số phần tử của M bằng:
A. 4
B. 5
C. 6
D. 10
