Tính:
a) \(\mathop {\lim }\limits_{n \to + \infty } \frac{{n - 1}}{{2n + 3}}\);
b) \(\mathop {\lim }\limits_{x \to {1^ + }} \frac{{\sqrt {{x^3} - {x^2}} }}{{\sqrt {x - 1} + 1 - x}}\).
Tính:
a) \(\mathop {\lim }\limits_{n \to + \infty } \frac{{n - 1}}{{2n + 3}}\);
b) \(\mathop {\lim }\limits_{x \to {1^ + }} \frac{{\sqrt {{x^3} - {x^2}} }}{{\sqrt {x - 1} + 1 - x}}\).
a) \(\mathop {\lim }\limits_{n \to + \infty } \frac{{n - 1}}{{2n + 3}} = \mathop {\lim }\limits_{n \to + \infty } \frac{{n\left( {1 - \frac{1}{n}} \right)}}{{n\left( {2 + \frac{3}{n}} \right)}}\) \( = \mathop {\lim }\limits_{n \to + \infty } \frac{{1 - \frac{1}{n}}}{{2 + \frac{3}{n}}} = \frac{{\mathop {\lim }\limits_{n \to + \infty } \left( {1 - \frac{1}{n}} \right)}}{{\mathop {\lim }\limits_{n \to + \infty } \left( {2 + \frac{3}{n}} \right)}} = \frac{1}{2}\).
b) \(\mathop {\lim }\limits_{x \to {1^ + }} \frac{{\sqrt {{x^3} - {x^2}} }}{{\sqrt {x - 1} + 1 - x}}\)\( = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{\sqrt {{x^2}\left( {x - 1} \right)} }}{{\sqrt {x - 1} - \left( {x - 1} \right)}}\)\( = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{x\sqrt {\left( {x - 1} \right)} }}{{\sqrt {x - 1} \left( {1 - \sqrt {x - 1} } \right)}}\)
\( = \mathop {\lim }\limits_{x \to {1^ + }} \frac{x}{{1 - \sqrt {x - 1} }} = \frac{1}{{1 - \sqrt {1 - 1} }} = 1.\)

Các bài tập cùng chuyên đề
Bài 1 :
Tính các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{9x + 1}}{{3x - 4}};\)
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{7x - 11}}{{2x + 3}};\)
c) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {{x^2} + 1} }}{x};\)
d) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^2} + 1} }}{x};\)
e) \(\mathop {\lim }\limits_{x \to {6^ - }} \frac{1}{{x - 6}};\)
g) \(\mathop {\lim }\limits_{x \to {7^ + }} \frac{1}{{x - 7}}.\)
Bài 2 :
Một công ty sản xuất máy tính đã xác định được rằng, tính trung bình một nhân viên có thể lắp ráp được \(N\left( t \right) = \frac{{50t}}{{t + 4}}\,\,\left( {t \ge 0} \right)\) bộ phận mỗi ngày sau t ngày đào tạo. Tính \(\mathop {\lim }\limits_{t \to + \infty } N\left( t \right)\) và cho biết ý nghĩa của kết quả.
Bài 3 :
Chi phí (đơn vị: nghìn đồng) để sản xuất x sản phẩm của một công ty được xác định bởi hàm số: C(x) = 50 000 + 105x.
a) Tính chi phí trung bình \(\overline C \left( x \right)\) để sản xuất một sản phẩm.
b) Tính \(\mathop {\lim }\limits_{x \to + \infty } \overline C \left( x \right)\) và cho biết ý nghĩa của kết quả.
Bài 4 :
Tính các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{6x + 8}}{{5x - 2}}\);
b) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{6x + 8}}{{5x - 2}}\);
c) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {9{x^2} - x + 1} }}{{3x - 2}}\);
d) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {9{x^2} - x + 1} }}{{3x - 2}}\);
e) \(\mathop {\lim }\limits_{x \to - {2^ - }} \frac{{3{x^2} + 4}}{{2x + 4}}\);
g) \(\mathop {\lim }\limits_{x \to - {2^ + }} \frac{{3{x^2} + 4}}{{2x + 4}}\).
Bài 5 :
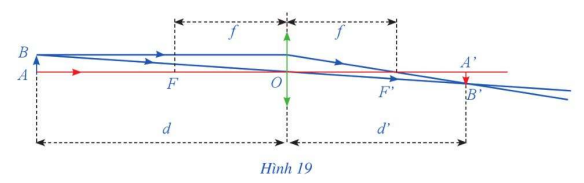
Một thấu kính hội tụ có tiêu cự là \(f\). Gọi \(d\) và \(d'\) lần lượt là khoảng cách từ một vật thật AB và từ ảnh \(A'B'\) của nó tới quang tâm \(O\) của thấu kính như Hình 19. Công thức thấu kính là \(\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f}\).
a) Tìm biểu thức xác định hàm số \(d' = \varphi (d)\).
b) Tìm \(\mathop {\lim }\limits_{d \to {f^ + }} \varphi (d),\mathop {\lim }\limits_{d \to {f^ - }} \varphi (d)\) và \(\mathop {\lim }\limits_{d \to f} \varphi (d)\). Giải thích ý nghĩa của các kết quả tìm được.
Bài 6 :
Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to - {1^ + }} \frac{1}{{x + 1}}\);
b) \(\mathop {\lim }\limits_{x \to - \infty } \left( {1 - {x^2}} \right)\);
c) \(\mathop {\lim }\limits_{x \to {3^ - }} \frac{x}{{3 - x}}\).
Bài 7 :
Trong hồ có chứa 6000 lít nước ngọt. Người ta bơm nước biển có nồng độ muối là 30 gam/lít vào hồ với tốc độ 15 lít/phút.
a) Chứng tỏ rằng nồng độ muối của nước trong hồ sau \(t\) phút kể từ khi bắt đầu bơm là \(C\left( t \right) = \frac{{30t}}{{400 + t}}\)(gam/lít).
b) Nồng độ muối trong hồ như thế nào nếu \(t \to + \infty \).
Bài 8 :
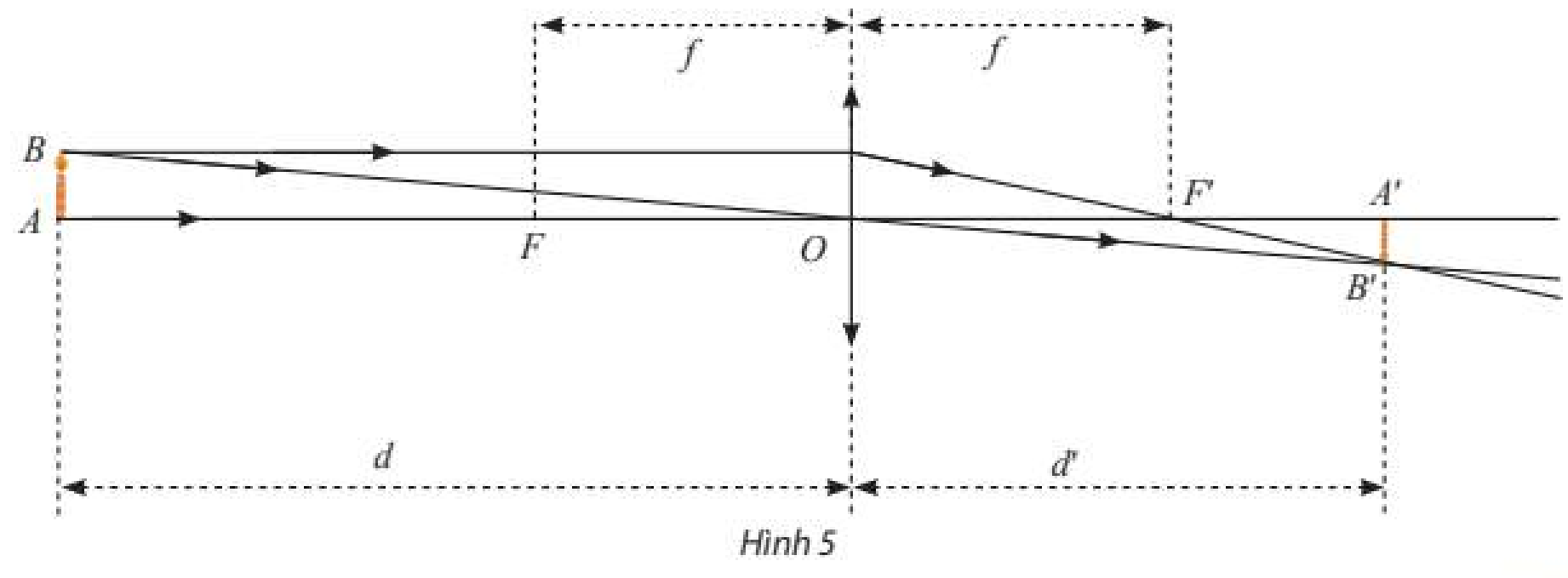
Một thấu kính hội tụ có tiêu cự là \(f > 0\) không đổi. Gọi \(d\) và \(d'\) lần lượt là khoảng cách từ vật thật và ảnh của nó tới quang tâm \(O\) của thấu kính (Hình 5). Ta có công thức: \(\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f}\) hay \(d' = \frac{{df}}{{d - f}}\).
Xét hàm số \(g\left( d \right) = \frac{{df}}{{d - f}}\). Tìm các giới hạn sau đây và giải thích ý nghĩa.
a) \(\mathop {\lim }\limits_{d \to {f^ + }} g\left( d \right)\);
b) \(\mathop {\lim }\limits_{d \to + \infty } g\left( d \right)\).
Bài 9 :
Sử dụng định nghĩa, tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to - 1} \left( {{x^3} - 3x} \right)\);
b) \(\mathop {\lim }\limits_{x \to 2} \sqrt {2x + 5} \);
c) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{4 - x}}{{2x + 1}}\).
Bài 10 :
Tìm giá trị của các tham số a và b, biết rằng:
a) \(\mathop {\lim }\limits_{x \to 2} \frac{{ax + b}}{{x - 2}} = 5\);
b) \(\mathop {\lim }\limits_{x \to 1} \frac{{a\sqrt x + b}}{{x - 1}} = 3\).
Bài 11 :
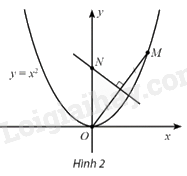
Trong mặt phẳng tọa độ Oxy, cho điểm \(M\left( {t,{t^2}} \right),t > 0\), nằm trên đường parabol \(y = {x^2}\). Đường trung trực của đoạn thẳng OM cắt trục tung tại N. Điểm N dần đến điểm nào khi M dần đến điểm O?
Bài 12 :
Biết \(\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 3x + a}}{{x - 1}} = b\) với a và b là hai số thực. Giá trị của \(a + b\) bằng
A. 1.
B. 2.
C. 4.
D. 5.
Bài 13 :
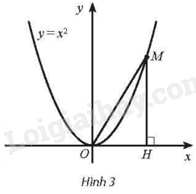
Cho điểm M thay đổi trên parabol \(y = {x^2}\); H là hình chiếu vuông góc của M trên trục hoành. Gọi x là hoành độ của điểm H. Tìm \(\mathop {\lim }\limits_{x \to + \infty } \left( {OM - MH} \right)\)
Bài 14 :
Giả sử \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = L\) và \(\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = M\) \(\left( {L,M \in \mathbb{R}} \right)\). Phát biểu nào sau đây là SAI?
A. \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right) + g\left( x \right)} \right] = L + M\)
B. \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right) - g\left( x \right)} \right] = L - M\)
C. \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right).g\left( x \right)} \right] = L.M\)
D. \(\mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{L}{M}\)
Bài 15 :
Quan sát đồ thị hàm số ở hình dưới đây và cho biết các giới hạn sau: \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\), \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right)\), \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} f\left( x \right)\), \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ - }} f\left( x \right)\).
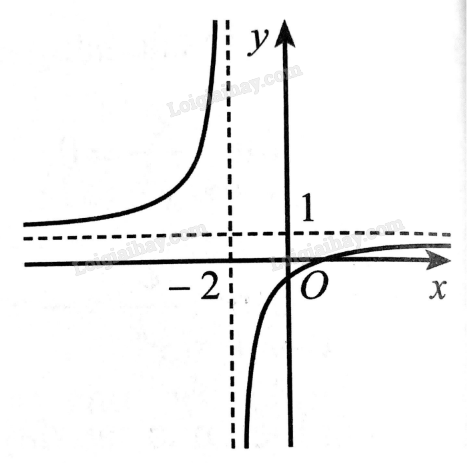
Bài 16 :
Tính các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to - 1} \left( { - 4{x^2} + 3x + 1} \right)\)
b) \(\mathop {\lim }\limits_{x \to - 1} \frac{{ - 4x + 1}}{{{x^2} - x + 3}}\)
c) \(\mathop {\lim }\limits_{x \to 2} \sqrt {3{x^2} + 5x + 4} \)
d) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{ - 3 + \frac{4}{x}}}{{2{x^2} + 3}}\)
e) \(\mathop {\lim }\limits_{x \to {2^ + }} \frac{{ - 3}}{{x - 2}}\)
g) \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} \frac{5}{{x + 2}}\)
Bài 17 :
Tính các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{ - 5x + 2}}{{3x + 1}}\)
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{ - 2x + 3}}{{3{x^2} + 2x + 5}}\)
c) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {9{x^2} + 3} }}{{x + 1}}\)
d) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {9{x^2} + 3} }}{{x + 1}}\)
e) \(\mathop {\lim }\limits_{x \to 1} \frac{{2{x^2} - 8x + 6}}{{{x^2} - 1}}\)
g) \(\mathop {\lim }\limits_{x \to - 3} \frac{{ - {x^2} + 2x + 15}}{{{x^2} + 4x + 3}}\)
Bài 18 :
Cho số thực \(a\) và hàm số \(f\left( x \right)\) thoả mãn \(\mathop {\lim }\limits_{x \to a} f\left( x \right) = - \infty \). Chứng minh rằng \(\mathop {\lim }\limits_{x \to a} \frac{{f\left( x \right) - 3}}{{2f\left( x \right) + 1}} = \frac{1}{2}\).
Bài 19 :
Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên biến đổi theo một hàm số thời gian (tính theo ngày) là \(g\left( t \right) = 45{t^2} - {t^3}\) (người). Tốc độ trung bình gia tăng người bệnh giữa hai thời điểm \({t_1}\), \({t_2}\) là \({V_{tb}} = \frac{{g\left( {{t_2}} \right) - g\left( {{t_1}} \right)}}{{{t_2} - {t_1}}}\). Tính \(\mathop {\lim }\limits_{t \to 10} \frac{{g\left( t \right) - g\left( {10} \right)}}{{t - 10}}\) và cho biết ý nghĩa kết quả tìm được.
Bài 20 :
Tính các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{2 + \frac{4}{{3x}}}}{{{x^2} - 1}}\)
b) \(\mathop {\lim }\limits_{x \to {2^ + }} \frac{1}{{x - 2}}\)
c) \(\mathop {\lim }\limits_{x \to - {3^ + }} \frac{{ - 5 + x}}{{x + 3}}\)
d) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{14x + 2}}{{ - 7x + 1}}\)
e) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{ - 2{x^2}}}{{3x + 5}}\)
g) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {4{x^2} + 1} }}{{x + 2}}\)
h) \(\mathop {\lim }\limits_{x \to 1} \frac{{x - 1}}{{{x^2} - 1}}\)
i) \(\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 5x + 6}}{{x - 2}}\)
k) \(\mathop {\lim }\limits_{x \to 3} \frac{{ - {x^2} + 4x - 3}}{{{x^2} + 3x - 18}}\)
Bài 21 :
Tính các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to 2} \frac{{\sqrt {4x + 1} - 3}}{{x - 2}};\)
b) \(\mathop {\lim }\limits_{x \to 1} \frac{{{x^3} + {x^2} + x - 3}}{{{x^3} - 1}};\)
c) \(\mathop {\lim }\limits_{x \to {2^ + }} \frac{{{x^2} - 5x + 6}}{{{{\left( {x - 2} \right)}^2}}};\)
d) \(\mathop {\lim }\limits_{x \to {0^ - }} \frac{{{x^2} + x - 2}}{x}.\)
Bài 22 :
Cho \(f(x) = \frac{{{x^2} - x}}{{|x|}}\). Khi đó, giới hạn \(\mathop {\lim }\limits_{x \to 0} f(x)\) là
A. 2
B. - 1
C. 1
D. Không tồn tại
Bài 23 :
Tính các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to - \infty } \frac{{x(x + 1)(2x - 1)}}{{5{x^3} + x + 7}}\);
b) \(\mathop {\lim }\limits_{x \to - \infty } ({x^3} - 1)(2 - {x^5})\);
c) \(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt[3]{{{x^2} + {x^2} + 1}} - x} \right)\).
Bài 24 :
Tính \(\mathop {\lim }\limits_{x \to 0} x\sin \frac{1}{x}\).
Bài 25 :
-
A.
\(\frac{1}{2}\).
-
B.
2.
-
C.
7.
-
D.
0.
Bài 26 :
Tính các giới hạn sau:
a) \(\mathop {\lim }\limits_{n \to + \infty } \left( {1 + n - {n^2}} \right).\)
b) \(\mathop {\lim }\limits_{x \to 2} \frac{{{x^3} - 8}}{{{x^2} - 4}}.\)
Bài 27 :
Cho hàm số $f\left( x \right)$ thỏa mãn $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2.$ Giá trị $\mathop {\lim }\limits_{x \to + \infty } 3f\left( x \right)$ bằng
-
A.
6.
-
B.
2.
-
C.
5.
-
D.
$\frac{3}{2}.$
Bài 28 :
Tính các giới hạn sau:
a) \(\mathop {\lim }\limits_{n \to + \infty } \left( {1 + n - {n^2}} \right)\);
b) \(\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {{x^2} + 4} - 2}}{x}\).
Bài 29 :
Cho $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = - \infty $, trong bốn khẳng định sau đây, khẳng định nào sai?
-
A.
Tồn tại số thực $a > 0$ sao cho $f\left( a \right) < 0$.
-
B.
\(\mathop {\lim }\limits_{x \to + \infty } \left[ { - f\left( x \right)} \right] = + \infty \).
-
C.
\(\mathop {\lim }\limits_{x \to + \infty } \frac{1}{{f\left( x \right)}} = 0\).
-
D.
\(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = + \infty \).
Bài 30 :
Cho các giới hạn: $\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = 2$; $\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = 3$, hỏi $\mathop {\lim }\limits_{x \to {x_0}} \left[ {3f\left( x \right) - 4g\left( x \right)} \right]$ bằng
-
A.
$5$.
-
B.
$2$.
-
C.
$ - 6$.
-
D.
$3$.


















Danh sách bình luận