Tung con xúc xắc cân đối liên tiếp hai lần. Xét các biến cố sau:
A: “Xuất hiện mặt một chấm ở lần gieo thứ nhất”;
B: “Xuất hiện mặt hai chấm ở lần gieo thứ hai”;
C: “Tổng số chấm xuất hiện ở hai lần gieo bằng 7”.
Chứng minh rằng:
a) Hai biến cố A và B độc lập;
b) Hai biến cố B và C độc lập;
c) Hai biến cố A và C độc lập.
Ý a: Liệt kê các biến cố và chứng minh \(P\left( {AB} \right) = P\left( A \right) \cdot P\left( B \right)\).
Ý b: Liệt kê các biến cố và chứng minh \(P\left( {BC} \right) = P\left( B \right) \cdot P\left( C \right)\).
Ý c: Liệt kê các biến cố và chứng minh \(P\left( {AC} \right) = P\left( A \right) \cdot P\left( C \right)\).
a) Ta có \(A = \left\{ {\left( {1,1} \right);\left( {1,2} \right);\left( {1,3} \right);\left( {1,4} \right);\left( {1,5} \right);\left( {1,6} \right)} \right\}\);
\(B = \left\{ {\left( {1,2} \right);\left( {2,3} \right);\left( {3,2} \right);\left( {4,2} \right);\left( {5,2} \right);\left( {6,2} \right)} \right\}\); \(AB = \left\{ {\left( {1,2} \right)} \right\}\)
Suy ra \(P\left( A \right) = \frac{6}{{36}} = \frac{1}{6};P\left( B \right) = \frac{6}{{36}} = \frac{1}{6};P\left( {AB} \right) = \frac{1}{6} \Rightarrow P\left( {AB} \right) = P\left( A \right) \cdot P\left( B \right)\).
Vậy hai biến cố A và B độc lập.
b) Ta có \(C = \left\{ {\left( {1,6} \right);\left( {2,5} \right);\left( {3,4} \right);\left( {4,3} \right);\left( {5,2} \right);\left( {6,1} \right)} \right\}\); \(BC = \left\{ {\left( {5,2} \right)} \right\}\).
Suy ra \(P\left( C \right) = \frac{6}{{36}} = \frac{1}{6} \Rightarrow P\left( {BC} \right) = P\left( B \right) \cdot P\left( C \right)\).
Vậy hai biến cố B và C độc lập.
c) Ta có \(AC = \left\{ {\left( {1,6} \right)} \right\}\) nên \(P\left( {AC} \right) = \frac{1}{6} \Rightarrow P\left( {AC} \right) = P\left( A \right) \cdot P\left( C \right)\).
Vậy hai biến cố A và C độc lập.

Các bài tập cùng chuyên đề
Bài 1 :
Trở lại tình huống mở đầu Mục 2. Thống kê cho thấy tỉ lệ dân số mắc bệnh hiểm nghèo X là 0,2%.
a) Trước khi tiến hành xét nghiệm, xác suất mắc bệnh hiểm nghèo X của ông M là bao nhiêu?
b) Sau khi xét nghiệm cho kết quả dương tính, xác suất mắc bệnh hiểm nghèo X của ông M là bao nhiêu?

Bài 2 :
Có hai đội thi đấu môn Bắn súng. Đội I có 5 vận động viên, đội II có 7 vận động viên. Xác suất đạt huy chương vàng của mỗi vận động viên đội I và đội II tương ứng là 0,65 và 0,55. Chọn ngẫu nhiên một vận động viên.
a) Tính xác suất để vận động viên này đạt huy chương vàng;
b) Giả sử vận động viên được chọn đạt huy chương vàng. Tính xác suất để vận động viên này thuộc đội I.
Bài 3 :
Một bộ lọc được sử dụng để chặn thư rác trong các tài khoản thư điện tử. Tuy nhiên, vì bộ lọc không tuyệt đối hoàn hảo nên một thư rác bị chặn với xác suất là 0,95 và một thư đúng (không phải là thư rác) bị chặn với xác suất 0,01. Thống kê cho thấy tỉ lệ thư rác là 3%.
a) Chọn ngẫu nhiên một thư bị chặn. Tính xác suất để đó là thư rác.
b) Chọn ngẫu nhiên một thư không bị chặn. Tính xác suất để đó là thư đúng.
c) Trong số các thư bị chặn, có bao nhiêu phần trăm là thư đúng? Trong số các thư không bị chặn, có bao nhiêu phần trăm là thư rác?
Bài 4 :
Có hai chuồng gà. Chuồng I có 8 con gà trống và 13 con gà mái. Chuồng II có 10 con gà trống và 6 con gà mái. An bắt ngẫu nhiên một con gà từ chuồng II đem thả vào chuồng I. Sau đó, Bình bắt ngẫu nhiên một con gà từ chuồng I.
Giả sử Bình bắt được con gà mái. Tính xác suất để Bình bắt được con gà mái ở chuồng I.
Bài 5 :
Trong một tuần, Sơn chọn ngẫu nhiên ba ngày chạy bộ buổi sáng. Nếu chạy bộ thì xác suất Sơn ăn thêm 1 quả trứng vào bữa sáng hôm đó là 0,7. Nếu không chạy bộ thì xác suất Sơn ăn thêm một quả trứng vào bữa sáng hôm đó là 0,25. Chọn ngẫu nhiên một ngày trong tuần của Sơn. Tính xác suất để hôm đó Sơn chạy bộ nếu biết rằng sáng hôm đó Sơn có ăn thêm một quả trứng.
Bài 6 :
Một hộp có 24 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, …, 24; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên 1 chiếc thẻ trong hộp. Xét biến cố A: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 3” và biến cố B: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4”.
a) Viết các tập con của không gian mẫu tương ứng với các biến cố A, B, \(A \cap B,A \cap \overline B \) (Hình 2).
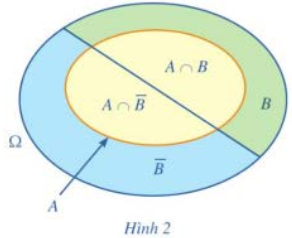
b) So sánh n(A) và \(n\left( {A \cap B} \right) + n\left( {A \cap \overline B } \right)\). Từ đó, hãy chứng tỏ rằng: \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right)\).
c) So sánh \(P\left( {A \cap B} \right)\) và \(P\left( B \right).P\left( {A|B} \right)\);
\(P\left( {A \cap \overline B } \right)\) và \(P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Từ đó, hãy chứng tỏ rằng: \(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Bài 7 :
Hãy giải bài toán mở đầu bằng phương pháp sử dụng sơ đồ hình cây như trong Ví dụ 3.
Bài 8 :
Được biết có 5% đàn ông bị mù màu, và 0,25% phụ nữ bị mù màu (Nguồn: F. M. Dekking et al., A modern introduction to probability and statistics – Understanding why and how, Springer, 2005). Giả sử số đàn ông bằng số phụ nữ. Chọn một người bị mù màu một cách ngẫu nhiên. Hỏi xác suất để người đó là đàn ông là bao nhiêu?
Bài 9 :
Có hai chiếc hộp, hộp I có 5 viên bi màu trắng và 5 viên bi màu đen, hộp II có 6 viên bi màu trắng và 4 viên bi màu đen, các viên bi có cùng kích thước và khối lượng. Lấy ngẫu nhiên một viên bi từ hộp I bỏ sang hộp II. Sau đó lấy ngẫu nhiên một viên bi từ hộp II.
a) Tính xác suất để viên bi được lấy ra là viên bi màu trắng.
b) Giả sử viên bi được lấy ra là viên bi màu trắng. Tính xác suất viên bi màu trắng đó thuộc hộp I.
Bài 10 :
Một loại linh kiện do hai nhà máy số I, số II cùng sản xuất. Tỉ lệ phế phẩm của các nhà máy I, II lần lượt là: 4%; 3%. Trong một lô linh kiện để lẫn lộn 80 sản phẩm của nhà máy số I và 120 sản phẩm của nhà máy số II. Một khách hàng lấy ngẫu nhiên một linh kiện từ lô hàng đó.
a) Tính xác suất để linh kiện được lấy ra là linh kiện tốt.
b) Giả sử linh kiện được lấy ra là linh kiện phế phẩm. Xác suất linh kiện đó do nhà máy nào sản xuất là cao hơn?
Bài 11 :
Năm 2001, Cộng đồng châu Âu có làm một đợt kiểm tra rất rộng rãi các con bò để phát hiện những con bị bệnh bò điên. Không có xét nghiệm nào cho kết quả chính xác 100%. Một loại xét nghiệm, mà ở đây ta gọi là xét nghiệm A, cho kết quả như sau: khi con bò bị bệnh bò điên thì xác suất để có phản ứng dương tính trong xét nghiệm A là 70%, còn khi con bò không bị bệnh thì xác suất để có phản ứng dương tính trong xét nghiệm A là 10%. Biết rằng tỉ lệ bò bị mắc bệnh bò điên ở Hà Lan là 13 con trên 1 000 000 con (Nguồn: F. M. Dekking et al., A modern introduction to probability and statistics – Understanding why and how, Springer, 2005). Hỏi khi một con bò ở Hà Lan có phản ứng dương tính với xét nghiệm A thì xác suất để nó bị mắc bệnh bò điên là bao nhiêu?
Bài 12 :
Một cửa hàng kinh doanh tổ chức rút thăm trúng thưởng cho hai loại sản phẩm. Tỉ lệ trúng thưởng của các loại sản phẩm I, II lần lượt là: 6%; 4%. Trong một hộp kín gồm các thăm cùng loại, người ta để lẫn lộn 200 chiếc thăm cho sản phẩm loại I và 300 chiếc thăm cho sản phẩm loại II. Một khách hàng lấy ngẫu nhiên 1 chiếc thăm từ chiếc hộp đó.
a) Tính xác suất để chiếc thăm được lấy ra là trúng thưởng.
b) Giả sử chiếc thăm được lấy ra là trúng thưởng. Xác suất chiếc thăm đó thuộc loại sản phẩm nào là cao hơn?
Bài 13 :
Giả sử trong một nhóm người có 2 người nhiễm bệnh, 58 người còn lại là không nhiễm bệnh. Để phát hiện ra người nhiễm bệnh, người ta tiến hành xét nghiệm tất cả mọi người của nhóm đó. Biết rằng đối với người nhiễm bệnh thì xác suất xét nghiệm có kết quả dương tính là 85%, nhưng đối với người không nhiễm bệnh thì xác suất xét nghiệm có phản ứng dương tính là 7%.
a) Vẽ sơ đồ hình cây biểu thị tình huống trên.
b) Giả sử X là một người trong nhóm bị xét nghiệm có kết quả dương tính. Tính xác suất để X là người nhiễm bệnh.
Bài 14 :
Khi phát hiện một vật thể bay, xác suất một hệ thống radar phát cảnh báo là 0,9 nếu vật thể bay đó là mục tiêu thật và là 0,05 nếu đó là mục tiêu giả. Có 99% các vật thể bay là mục tiêu giả. Biết rằng hệ thống radar đang phát cảnh báo khi phát hiện một vật thể bay. Tính xác suất vật thể đó là mục tiêu thật.

Bài 15 :
Người ta điều tra thấy ở một địa phương nọ có 2% tài xế sử dụng điện thoại di động khi lái xe. Trong các vụ tai nạn ở địa phương đó, người ta nhận thấy có 10% là do tài xế có sử dụng điện thoại khi lái xe gây ra. Hỏi việc sử dụng điện thoại di động khi lái xe làm tăng xác suất gây tai nạn lên bao nhiêu lần?
Bài 16 :
Hộp thứ nhất có 3 viên bi xanh và 6 viên bi đỏ. Hộp thứ hai có 3 viên bi xanh và 7 viên bi đỏ. Các viên bi có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên 1 viên bi từ hộp thứ nhất chuyển sang hộp thứ hai. Sau đó lại lấy ra ngẫu nhiên đồng thời 2 viên bi từ hộp thứ hai.
a) Tính xác suất để hai viên bi lấy ra từ hộp thứ hai là bi đỏ.
b) Biết rằng 2 viên bi lấy ra từ hộp thứ hai là bi đỏ, tính xác suất viên bi lấy ra từ hộp thứ nhất cũng là bi đỏ.
Bài 17 :
Trong một trường học, tỉ lệ học sinh nữ là 52%. Tỉ lệ học sinh nữ và tỉ lệ học sinh nam tham gia câu lạc bộ nghệ thuật lần lượt là 18% và 15%. Chọn ngẫu nhiên 1 học sinh của trường.
a) Tính xác suất học sinh được chọn có tham gia câu lạc bộ nghệ thuật.
b) Biết rằng học sinh được chọn có tham gia câu lạc bộ nghệ thuật. Tính xác suất học sinh đó là nam.
Bài 18 :
Tỉ lệ người dân đã tiêm vắc xin phòng bệnh A ở một địa phương là 65%. Trong số những người đã tiêm phòng, tỉ lệ mắc bệnh A là 5%; trong số những người chưa tiêm phòng, tỉ lệ mắc bệnh A là 17%. Chọn ngẫu nhiên một người ở địa phương đó.
a) Tính xác suất người được chọn mắc bệnh A.
b) Biết rằng người được chọn mắc bệnh A. Tính xác suất người đó chưa tiêm vắc xin phòng bệnh A.
Bài 19 :
Ở một khu rừng nọ có 7 chú lùn, trong đó có 4 chú luôn nói thật, 3 chú còn lại luôn tự nhận mình nói thật nhưng xác suất để mỗi chú này nói thật là 0,5. Bạn Tuyết gặp ngẫu nhiên 1 chú lùn. Gọi \(A\) là biến cố “Chú lùn đó luôn nói thật” và \(B\) là biến cố “Chú lùn đó tự nhận mình luôn nói thật”.
a) Tính xác suất của các biến cố \(A\) và \(B\).
b) Biết rằng chú lùn mà bạn Tuyết gặp tự nhận mình là người luôn nói thật. Tính xác suất để chú lùn đó luôn nói thật.
Bài 20 :
Cho sơ đồ hình cây dưới đây.
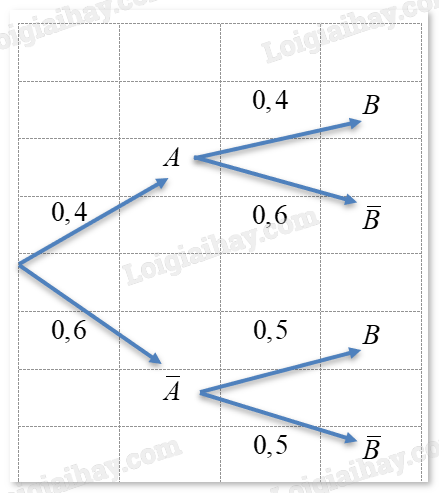
a) Xác suất của biến cố cả \(A\) và \(B\) đều không xảy ra là
A. \(0,32\)
B. \(0,4\)
C. \(0,8\)
D. \(0,92\)
b) Xác suất của biến cố \(B\) là
A. \(0,42\)
B. \(0,62\)
C. \(0,28\)
D. \(0,48\)
c) Xác suất điều kiện \(P\left( {A|B} \right)\) là
A. \(\frac{7}{{31}}\)
B. \(0,7\)
C. \(\frac{7}{{50}}\)
D. \(0,48\)
d) Giá trị của biểu thức \(\frac{{P\left( B \right)P\left( {\bar A|B} \right)}}{{P\left( {\bar A} \right)}}\) là
A. \(0,48\)
B. \(0,3\)
C. \(0,5\)
D. \(0,6\)
Bài 21 :
Hộp thứ nhất có 1 viên bi xanh và 5 viên bi đỏ, hộp thứ hai có 3 viên bi xanh và 5 viên bi đỏ. Các viên bi có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên đồng thời 2 viên bi từ hộp thứ nhất chuyển sang hộp thứ hai. Sau đó lại lấy ra ngẫu nhiên đồng thời 2 viên bi ở hộp thứ hai.
a) Tính xác suất để hai viên bi lấy ra ở hộp thứ hai là bi đỏ.
b) Biết rằng 2 viên bi lấy ra từ hộp thứ hai là bi đỏ. Tính xác suất để hai viên bi lấy ra từ hộp thứ nhất cũng là bi đỏ.
Bài 22 :
Một doanh nghiệp có 45% nhân viên là nữ. Tỉ lệ nhân viên nữ và tỉ lệ nhân viên nam mua bảo hiểm nhân thọ lần lượt là 7% và 5%. Chọn ngẫu nhiên một nhân viên của doanh nghiệp.
a) Tính xác suất nhân viên được chọn có mua bảo hiểm nhân thọ.
b) Biết rằng nhân viên được chọn có mua bảo hiểm nhân thọ. Tính xác suất nhân viên đó là nam.
Bài 23 :
Một xí nghiệp mỗi ngày sản xuất ra 1 600 sản phẩm, trong đó có 35 sản phẩm lỗi. Lần lượt lấy ra ngẫu nhiên 2 sản phẩm không hoàn lại để kiểm tra. Tính xác suất của các biến cố:
\(A\): “Sản phẩm lấy ra lần thứ hai không bị lỗi, biết sản phẩm lấy ra lần thứ nhất không bị lỗi”;
\(B\): “Sản phẩm lấy ra lần thứ hai bị lỗi, biết sản phẩm lấy ra lần thứ nhất không bị lỗi”,
\(C\): “Sản phẩm lấy ra lần thứ hai không bị lỗi, biết sản phẩm lấy ra lần thứ nhất bị lỗi”;
\(D\): “Sản phẩm lấy ra lần thứ hai bị lỗi, biết sản phẩm lấy ra lần thứ nhất bị lỗi”;
\(E\): “Sản phẩm lấy ra lần thứ hai bị lỗi”.
Bài 24 :
Trong mỗi ý a), b), c), d), chọn phương án: đúng (Đ) hoặc sai (S).
Cho các biến cố \(A,B\) thoả mãn \(0 < P\left( A \right) < 1,0 < P\left( B \right) < 1\).
a) \(P\left( B \right) = P\left( A \right).P\left( {B|A} \right) + P\left( {\overline A } \right).P\left( {B|\overline A } \right)\).
b) \(P\left( {A|B} \right) = \frac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}}\).
c) \(P\left( {A|B} \right) = \frac{{P\left( B \right).P\left( {B|A} \right)}}{{P\left( A \right)}}\).
d) \(P\left( A \right) = P\left( {A|B} \right)\).
Bài 25 :
Giả sử trong một nhóm 80 người có 69 người không nhiễm bệnh và 11 người nhiễm bệnh. Để phát hiện ra người nhiễm bệnh, người ta tiến hành xét nghiệm tất cả mọi người của nhóm đó. Biết rằng đối với người nhiễm bệnh, xác suất xét nghiệm có kết quả dương tính là 0,9; còn đối với người không nhiễm bệnh, xác suất xét nghiệm có kết quả dương tính là 0,05.
a) Vẽ sơ đồ hình cây biểu thị tình huống trên.
b) Giả sử X là một người trong nhóm bị xét nghiệm có kết quả dương tính. Tính xác suất để X là người nhiễm bệnh.
Bài 26 :
Cho hai biến cố độc lập \(A\) và \(B\) có \(P\left( A \right) = 0,4;P\left( B \right) = 0,8\). Tính \(P\left( {A|A \cup B} \right)\). Làm tròn kết quả đến hàng phần trăm.
Bài 27 :
Cho hai biến cố \(A\) và \(B\) có \(P\left( A \right) = 0,4;P\left( {B|\overline A } \right) = 0,2;P\left( {B|A} \right) = 0,3\). Tính \(P\left( {A|\overline B } \right)\).
Bài 28 :
Bạn Minh có 2 hộp đựng thẻ. Hộp thứ nhất có 4 thẻ vàng và 1 thẻ đỏ. Hộp thứ hai có 6 thẻ vàng và 2 thẻ đỏ. Các thẻ có cùng kích thước. Minh chọn ngẫu nhiên từ hộp thứ nhất ra 2 thẻ và bỏ vào hộp thứ hai. Sau đó, Minh lại chọn ngẫu nhiên từ hộp thứ hai ra 2 thẻ.
a) Tính xác suất để 2 thẻ được chọn ra từ hộp thứ hai đều có màu đỏ.
b) Biết rằng 2 thẻ được chọn ra từ hộp thứ hai đều có màu đỏ, tính xác suất của biến cố 2 thẻ lấy ra từ hộp thứ nhất có cùng màu.
Bài 29 :
Điều tra ở một khu vực cho thấy có 35% tài xế xe ô tô là nữ. Có 12% tài xế nữ sử dụng xe 7 chỗ và 25% tài xế nam sử dụng xe 7 chỗ. Chọn ngẫu nhiên 1 tài xế ở khu vực đó.
a) Tính xác suất tài xế đó sử dụng xe 7 chỗ.
b) Biết tài xế sử dụng xe 7 chỗ, tính xác suất đó là tài xế nam.
Bài 30 :
Một công ty công nghệ cung cấp hai phiên bản Basic và Pro của một phần mềm. Tỉ lệ người sử dụng hai phiên bản này lần lượt là 80% và 20%. Kết quả điều tra cho thấy có 30% người dùng phiên bản Basic sẽ mua bản cập nhật sau 1 năm sử dụng; còn tỉ lệ này của phiên bản Pro là 50%.
Chọn ngẫu nhiên một người sử dụng phần mềm trên của công ty.
a) Tính xác suất để người này mua bản cập nhật sau 1 năm sử dụng.
b) Biết người dùng mua bản cập nhật sau 1 năm sử dụng, tính xác suất người đó sử dụng phiên bản Basic ở năm đầu tiên.


















Danh sách bình luận