Đề bài

Từ một đỉnh tháp người ta nhìn hai điểm \(A\) và \(B\) trên mặt đất dưới các góc nhìn là \(\alpha  = {72^0}12'\) và \(\beta  = {34^0}26'\). Ba điểm \(A,B,C\) thẳng hàng trong đó C là điểm chính giữa chân tháp. Tính chiều cao CD của tháp biết \(AB = 91m\).

  

Lời giải của GV Loigiaihay.com

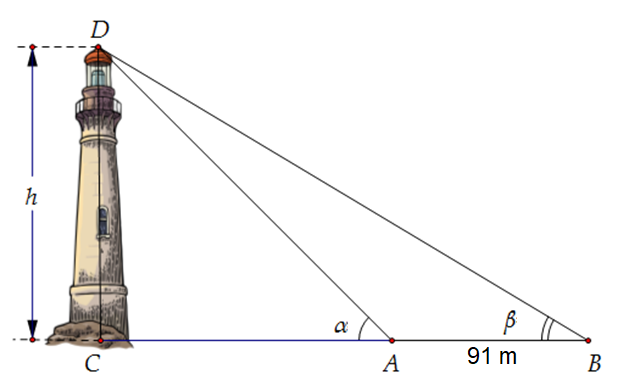
Ta có: \(\widehat {DAB} = {180^ \circ } - \alpha  = {180^ \circ } - {72^ \circ }12' = {107^ \circ }48'\); \(\widehat {ADB} = \widehat {DAC} - \widehat {DBA} = \alpha  - \beta  = {72^ \circ }12' - {34^ \circ }26' = {37^ \circ }46'\).

Áp dụng định lí sin trong tam giác DAB ta có:

\(\begin{array}{l}\frac{{AB}}{{\sin D}} = \frac{{DB}}{{\sin A}} \Leftrightarrow \frac{{91}}{{\sin {{37}^ \circ }46'}} = \frac{{DB}}{{\sin {{107}^ \circ }48'}}\\ \Rightarrow DB = \sin {107^ \circ }48'.\frac{{91}}{{\sin {{37}^ \circ }46'}}\end{array}\)

Lại có: tam giác DCB vuông tại C, suy ra \(CD = \sin B.DB\)

\( \Rightarrow CD = \sin {34^ \circ }26'.DB = \sin {34^ \circ }26'.\sin {107^ \circ }48'.\frac{{91}}{{\sin {{37}^ \circ }46'}} \approx 80\).

Vậy tháp đó cao khoảng 80m.