Cho hàm số liên tục trên các khoảng \(( - \infty ;1)\),\((1; + \infty )\)và có bảng biến thiên như sau

Xác định các khoảng đơn điệu và cực trị của hàm số đã cho.
- Để xác định khoảng đơn điệu của hàm số ta áp dụng định lý:
Cho hàm số \(y = f(x)\) có đạo hàm trên khoảng\(y = f(x)\), (có thể a là\( - \infty \) , b là \( + \infty \))
Nếu \(f'(x) > 0\) với mọi \(x \in (a;b)\) thì hàm số đồng biến trên khoảng \((a;b)\)
Nếu \(f'(x) < 0\) với mọi \(x \in (a;b)\) thì hàm số nghịch biến trên khoảng \((a;b)\)
- Để xác định cực trị của hàm số đã cho ta áp dụng mối liên hệ giữa sự tồn tại giữa cực trị và dấu của đạo hàm ở hoạt động 4 (Trang 6): Nếu đạo hàm có cực trị thì dấu của đạo hàm bên trái và bên phải điểm cực trị sẽ khác nhau.
Theo bảng biến thiên ta có:
- Hàm số \(y = f(x)\) đồng biến trên các khoảng là \(( - \infty ;1)\) , (2;3) , (3,4) , \((5; + \infty )\)
- Hàm số \(y = f(x)\) nghịch biến trên các khoảng là (1;2) , (4;5)
- Hàm số \(y = f(x)\) có các điểm cực trị là 2 và 5

Các bài tập cùng chuyên đề
Bài 1 :
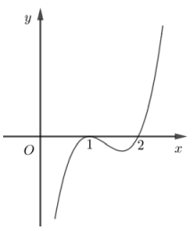
Hình dưới là đồ thị hàm số \(y = f'\left( x \right)\). Hỏi hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
-
A.
\(\left( {0;1} \right)\) và \(\left( {2; + \infty } \right)\)
-
B.
\(\left( {1;2} \right)\)
-
C.
\(\left( {2; + \infty } \right)\)
-
D.
\(\left( {0;1} \right)\)
Bài 2 :
Trong tất cả các giá trị của tham số $m$ để hàm số $y = \dfrac{1}{3}{x^3} + m{x^2} - mx - m$ đồng biến trên $R$, giá trị nhỏ nhất của $m$ là:
-
A.
$ - 4$
-
B.
$ - 1$
-
C.
$0$
-
D.
$1$
Bài 3 :
Tìm $m$ để hàm số $y = \dfrac{{{x^3}}}{3} - 2m{x^2} + 4mx + 2$ nghịch biến trên khoảng $\left( { - 2;0} \right)$.
-
A.
$m < - \dfrac{1}{3}$
-
B.
$m \leqslant - \dfrac{1}{3}$
-
C.
$m \leqslant - \dfrac{4}{3}$
-
D.
$m \leqslant 0$
Bài 4 :
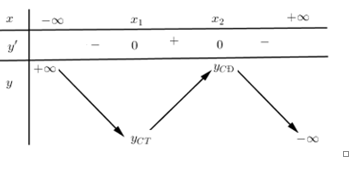
Cho bảng biến thiên hình bên, hàm số nghịch biến trên:
-
A.
$\left( {{x_1};{x_2}} \right)$
-
B.
$\left( { - \infty ;{x_1}} \right)$
-
C.
$\left( {{x_1}; + \infty } \right)$
-
D.
$\left( { - \infty ;{x_2}} \right)$
Bài 5 :
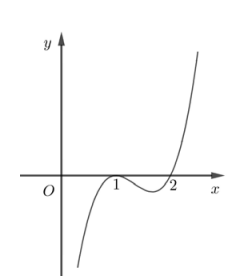
Hình bên là đồ thị hàm số \(y = f'\left( x \right)\) Hỏi hàm số \(y = f\left( x \right)\) nghịch biến trên khoảng nào dưới đây?
-
A.
\(\left( {2;3} \right)\)
-
B.
\(\left( {1; + \infty } \right)\)
-
C.
\(\left( {2; + \infty } \right)\)
-
D.
\(\left( { - \infty ;2} \right)\)
Bài 6 :
Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y = mx - \sin x$ đồng biến trên $\mathbb{R}.$
-
A.
$m > 1.$
-
B.
$m \le - 1.$
-
C.
$m \ge 1.$
-
D.
$m \ge - 1.$
Bài 7 :
Tìm tất cả các giá trị của tham số m để hàm số $y = {x^3} + {x^2} + mx + 1$ đồng biến trên khoảng $\left( { - \infty ; + \infty } \right)$
-
A.
$m \geqslant \dfrac{4}{3}$
-
B.
$m \leqslant \dfrac{4}{3}$
-
C.
$m \geqslant \dfrac{1}{3}$
-
D.
$m \leqslant \dfrac{1}{3}$
Bài 8 :
Tập hợp tất cả các giá trị của m để hàm số $y = \dfrac{1}{3}{x^3} - \left( {m - 1} \right){x^2} + 2\left( {m - 1} \right)x - 2$ luôn tăng trên $R$
-
A.
$m > 1$
-
B.
$\left[ {\begin{array}{*{20}{l}}{m < 1}\\{m > 3}\end{array}} \right.$
-
C.
$2 \le m \le 3$
-
D.
$1 \le m \le 3$
Bài 9 :
Tìm $m$ để hàm số $y = {x^3} - 3{x^2} + mx + 2$ tăng trên khoảng $\left( {1; + \infty {\rm{\;}}} \right).$
-
A.
$m \ge 3.$
-
B.
$m \ne 3.$
-
C.
$m \le 3.$
-
D.
$m < 3.$
Bài 10 :
Hàm số $y = {x^3} - 6{x^2} + mx + 1$ đồng biến trên $\left( {0; + \infty {\rm{\;}}} \right)$ khi giá trị của $m$ là:
-
A.
$m \ge 12$
-
B.
$m \le 12$
-
C.
$m \ge 0$
-
D.
$m \le 0$
Bài 11 :
Tìm các giá trị của tham số $m$ để hàm số $y = - {\mkern 1mu} {x^3} + m{x^2} - m$ đồng biến trên khoảng $\left( {1;2} \right).$
-
A.
$\left( {\dfrac{3}{2};3} \right).$
-
B.
$\left( { - {\mkern 1mu} \infty ;\dfrac{3}{2}} \right).$
-
C.
$\left[ {3; + {\mkern 1mu} \infty } \right).$
-
D.
$\left( { - {\mkern 1mu} \infty ;3} \right].$
Bài 12 :
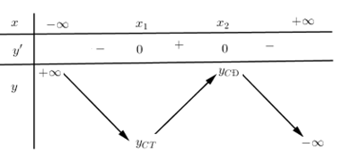
Cho bảng biến thiên hình bên, hàm số đồng biến trên:
-
A.
\(\left( {{x_1};{x_2}} \right)\)
-
B.
\(\left( { - \infty ;{x_1}} \right)\)
-
C.
\(\left( {{x_1}; + \infty } \right)\)
-
D.
\(\left( { - \infty ;{x_2}} \right)\)
Bài 13 :
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?

-
A.
\(\left( {0;1} \right)\)
-
B.
\(\left( { - \infty ; - 1} \right)\)
-
C.
\(\left( { - 1;1} \right)\)
-
D.
\(\left( { - 1;0} \right)\)
Bài 14 :
Tập hợp tất cả các giá trị thực của tham số m để hàm số \(y = - {x^3} - 6{x^2} + \left( {4m - 9} \right)x + 4\) nghịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\) là:
-
A.
\(\left( { - \infty ;0} \right]\)
-
B.
\(\left[ { - \dfrac{3}{4}; + \infty } \right)\)
-
C.
\(\left( { - \infty ; - \dfrac{3}{4}} \right]\)
-
D.
\(\left[ {0; + \infty } \right)\)
Bài 15 :
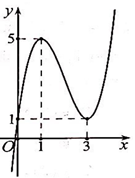
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Hàm số \(y = f\left( x \right)\) nghịch biến trên khoảng nào trong các khoảng sau?
-
A.
\(\left( {0;1} \right)\).
-
B.
\(\left( {1;5} \right)\).
-
C.
\(\left( {3; + \infty } \right)\).
-
D.
\(\left( {1;2} \right)\).
Bài 16 :
Tập tất cả giá trị của tham số \(m\) để hàm số \(y = {x^3} - 3m{x^2} + 3x + 1\) đồng biến trên \(\mathbb{R}\) là
-
A.
\(\left[ { - 1;\,1} \right]\).
-
B.
\(m \in \left( { - \infty ;\, - 1} \right] \cup \left[ {1;\, + \infty } \right)\).
-
C.
\(\left( { - \infty ;\, - 1} \right) \cup \left( {1;\, + \infty } \right)\).
-
D.
\(\left( { - 1;\,1} \right)\).
Bài 17 :
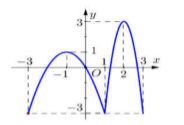
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên.
Hàm số đã cho nghịch biến trên khoảng:
-
A.
\(\left( {0;\,\,2} \right)\)
-
B.
\(\left( { - 2;\,0} \right)\)
-
C.
\(\left( { - 3; - 1} \right)\)
-
D.
\(\left( {2;\,3} \right)\)
Bài 18 :
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên:

Hàm số \(y = - 2f\left( x \right)\) đồng biến trên khoảng
-
A.
\(\left( {1;2} \right)\)
-
B.
\(\left( {2;3} \right)\)
-
C.
\(\left( { - 1;0} \right)\)
-
D.
\(\left( { - 1;1} \right)\)
Bài 19 :
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu \(f'\left( x \right)\) như sau:

Hàm số \(y = f\left( {2 - 3x} \right)\) đồng biến trên khoảng nào sau đây?
-
A.
\(\left( {1;3} \right)\)
-
B.
\(\left( {1;2} \right)\)
-
C.
\(\left( {2;3} \right)\)
-
D.
\(\left( {0;1} \right)\)
Bài 20 :
Tập tất cả các giá trị của tham số \(m\) để hàm số \(y = \dfrac{1}{3}{x^3} + 2{x^2} - mx\) đồng biến trên \(\mathbb{R}\) là:
-
A.
\(\left( { - 4; + \infty } \right)\)
-
B.
\(\left[ { - 4; + \infty } \right)\)
-
C.
\(\left( { - \infty ; - 4} \right)\)
-
D.
\(\left( { - \infty ; - 4} \right]\)
Bài 21 :
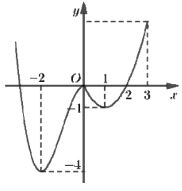
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ sau. Hàm số đã cho nghịch biến trên khoảng:
-
A.
\(\left( { - 1;\,\,0} \right)\)
-
B.
\(\left( { - 2; - 1} \right)\)
-
C.
\(\left( {0;\,\,1} \right)\)
-
D.
\(\left( {1;\,\,3} \right)\)
Bài 22 :
Đề thi THPT QG - 2021 - mã 101
Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
-
A.
\(\left( {0;1} \right)\)
-
B.
\(\left( { - \infty ;0} \right)\)
-
C.
\(\left( {0; + \infty } \right)\)
-
D.
\(\left( { - 1;1} \right)\)
Bài 23 :
Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
-
A.
\(\left( { - \infty ;2} \right)\)
-
B.
\(\left( {0;2} \right)\)
-
C.
\(\left( { - 2;2} \right)\)
-
D.
\(\left( {2; + \infty } \right)\)
Bài 24 :
Đề thi THPT QG - 2021 - mã 102
Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
-
A.
\(\left( { - 1;1} \right)\)
-
B.
\(\left( { - \infty ;0} \right)\)
-
C.
\(\left( {0;1} \right)\)
-
D.
\(\left( {0; + \infty } \right)\)
Bài 25 :
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
-
A.
\(\left( { - 1;1} \right)\)
-
B.
\(\left( {1; + \infty } \right)\)
-
C.
\(\left( { - \infty ;1} \right)\)
-
D.
\(\left( {0;3} \right)\)
Bài 26 :
Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số \(y = {x^3} - 3\left( {2m + 1} \right){x^2} + \left( {12m + 5} \right)x + 2\) đồng biến trên khoảng \(\left( {2; + \infty } \right).\) Số phần tử của \(S\) bằng:
-
A.
\(1\)
-
B.
\(2\)
-
C.
\(3\)
-
D.
\(0\)
Bài 27 :
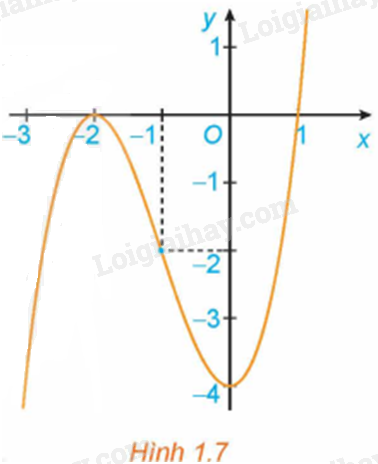
Quan sát đồ thị của hàm số \(y = {x^3} + 3{x^2} - 4\) (H.1.7). Xét dấu đạo hàm của hàm số đã cho và hoàn thành các bảng sau vào vở:
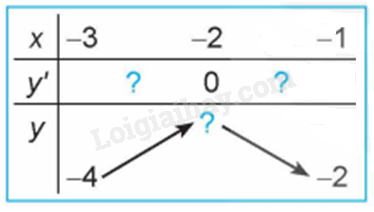
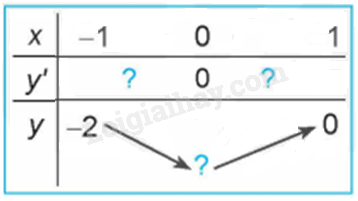
Bài 28 :
Xét sự đồng biến, nghịch biến của các hàm số sau:
a) \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x + 1\);
b) \(y = - {x^3} + 2{x^2} - 5x + 3\).
Bài 29 :
Tìm các khoảng đơn điệu của các hàm số sau:
a) \(y = \frac{{2x - 1}}{{x + 2}}\);
b) \(y = \frac{{{x^2} + x + 4}}{{x - 3}}\).
Bài 30 :
Xét chiều biến thiên của các hàm số sau:
a) \(y = \sqrt {4 - {x^2}} \);
b) \(y = \frac{x}{{{x^2} + 1}}\).


















Danh sách bình luận