Cho tam giác ABC có AB=12cm, AC=15cm. Trên các tia AB, AC lần lượt lấy các điểm M, N sao cho AM=10cm, AN=8cm. Chứng minh rằng ΔABC ∽ ΔANM.
- Chứng minh: \(\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}}\)
- Chứng minh hai tam giác ABC và tam giác ANM có hai cạnh tương ứng tỉ lệ và góc A chung nên hai tam giác ABC và tam giác ANM đồng dạng với nhau.
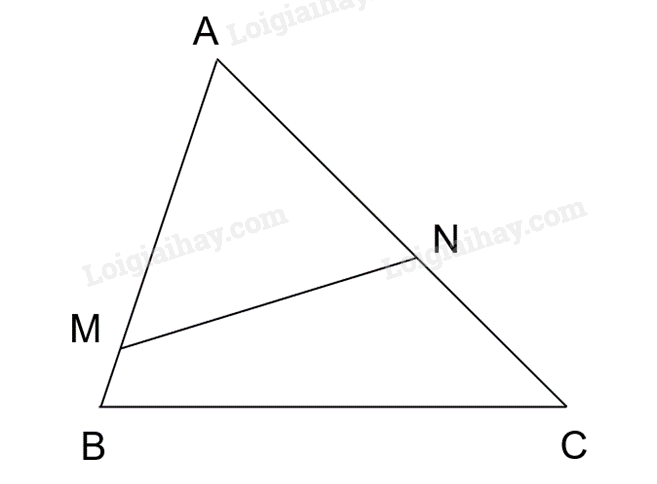
Có AB=12cm , AN=8cm => \(\frac{{AN}}{{AB}} = \frac{8}{{12}} = \frac{2}{3}\)
AC=15cm, AM=10cm => \(\frac{{AM}}{{AC}} = \frac{{10}}{{15}} = \frac{2}{3}\)
=> \(\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}}\)
- Xét hai tam giác ABC và tam giác ANM, có
\(\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}}\), góc A chung
=> ΔABC ∽ ΔANM (c.g.c)

Các bài tập cùng chuyên đề
Bài 1 :
Hai tam giác đồng dạng với nhau theo trường hợp cạnh – góc – cạnh nếu
-
A.
hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia.
-
B.
hai góc của tam giác này lần lượt bằng hai góc của tam giác kia.
-
C.
một cạnh của tam giác này bằng một cạnh của tam giác kia và một cặp góc bằng nhau.
-
D.
hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau.
Bài 2 :
Cho \(\Delta D{\rm{EF}}\) và \(\Delta ILK\) , biết DE = 10cm ; EF = 4cm ; IL = 20cm ; LK = 8cm cần thêm điều kiện gì để \(\Delta D{\rm{EF}} \backsim \Delta {\rm{ILK(c - g - c)?}}\)
-
A.
\(\hat E = \hat I.\)
-
B.
\(\hat E = \hat L\)
-
C.
\(\hat P = \hat I.\)
-
D.
\(\hat F = \hat K\)
Bài 3 :
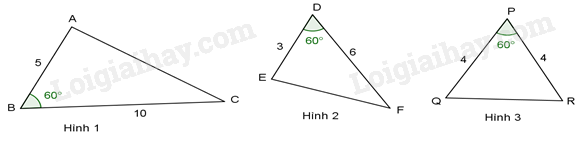
Hãy chỉ ra cặp tam giác đồng dạng với nhau từ các tam giác sau đây.
-
A.
Hình 1 và hình 2.
-
B.
Hình 2 và hình 3.
-
C.
Hình 1 và hình 3.
-
D.
Hình 1, hình 2 và hình 3.
Bài 4 :
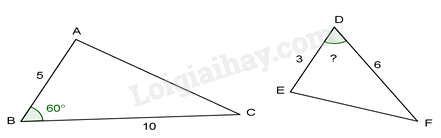
Để hai tam giác ABC và DEF đồng dạng thì số đo \(\hat D\) trong hình vẽ dưới bằng
-
A.
\({50^0}\)
-
B.
\({60^0}\)
-
C.
\({30^0}\)
-
D.
\({70^0}\)
Bài 5 :
Cho \(\Delta {A'}{B'}{C'}\) và \(\Delta ABC\) có \(\hat A = {\hat A'}\) . Để \(\Delta {A'}{B}{C'} \backsim \Delta ABC\) cần thêm điều kiện là:
-
A.
\(\frac{{{A'}{B'}}}{{AB}} = \frac{{{A'}{C'}}}{{AC}}.\)
-
B.
\(\frac{{{A'}{B'}}}{{AB}} = \frac{{{B'}{C'}}}{{BC}}.\)
-
C.
\(\frac{{{A'}{B'}}}{{AB}} = \frac{{BC}}{{{B'}{C'}}}.\)
-
D.
\(\frac{{{B'}{C'}}}{{BC}} = \frac{{AC}}{{{A'}{C'}}}.\)
Bài 6 :
Cho \(\Delta ABC\) và \(\Delta DEF\) có \(\hat B = \hat E\) , \(\frac{{BA}}{{BC}} = \frac{{DE}}{{EF}}\) thì:
-
A.
\(\Delta ABC \backsim \Delta DEF.\)
-
B.
\(\Delta ABC \backsim \Delta EDF.\)
-
C.
\(\Delta BAC \backsim \Delta DFE.\)
-
D.
\(\Delta ABC \backsim \Delta FDE.\)
Bài 7 :
Cho \(\Delta MNP \backsim \Delta KIH\) , biết \(\hat M = \hat K,MN = 2cm,MP = 8cm,KH = 4cm\) , thì KI bằng bao nhiêu:
-
A.
\(KI = 2cm.\)
-
B.
\(KI = 6cm.\)
-
C.
\(KI = 4cm.\)
-
D.
\(KI = 1cm.\)
Bài 8 :
Hãy chọn câu đúng. Nếu \(\Delta ABC\) và \(\Delta DEF\) có \(\hat B = \hat E\) , \(\frac{{BA}}{{DE}} = \frac{{BC}}{{EF}}\) thì
-
A.
\(\Delta ABC \backsim \Delta DEF.\)
-
B.
\(\Delta ABC \backsim \Delta EDF.\)
-
C.
\(\Delta BCA \backsim \Delta DFE.\)
-
D.
\(\Delta ABC \backsim \Delta FDE.\)
Bài 9 :
Cho \(\Delta ABC\) , lấy hai điểm D và E lần lượt nằm bên cạnh AB và AC sao cho \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}.\) Kết luận nào sau đây sai:
-
A.
\(\Delta ADE \backsim \Delta ABC.\)
-
B.
\(DE//BC.\)
-
C.
\(\frac{{AE}}{{AB}} = \frac{{AD}}{{AC}}.\)
-
D.
\(\widehat {ADE} = \widehat {ABC.}\)
Bài 10 :
Cho \(\Delta ABC\) , có AC = 18cm; AB = 9cm; BC = 15cm. Trên cạnh AC lấy điểm N sao cho AN = 3cm, trên cạnh AB lấy điểm M sao cho AM = 6cm. Tính độ dài đoạn thẳng MN:
-
A.
MN= 6cm
-
B.
MN = 5cm
-
C.
MN = 8cm
-
D.
MN = 9cm
Bài 11 :
Cho \(\Delta ABC\) , trên cạnh AB lấy điểm D khác A, B. Qua D kẻ đường thẳng song song với BC cắt AC tại E. Chọn kết luận sai:
-
A.
\(\Delta ADE \backsim \Delta ABC.\)
-
B.
\(DE//BC.\)
-
C.
\(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}.\)
-
D.
\(\widehat {ADE} = \widehat {ACB.}\)
Bài 12 :
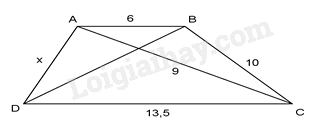
Với AB//CD thì giá trị của x trong hình vẽ dưới đây là
-
A.
x = 15
-
B.
x = 16
-
C.
x = 7
-
D.
x = 8
Bài 13 :
Cho hình thang vuông \(ABCD(\hat A = \hat D = {90^0})\) có AB = 16cm, CD = 25cm,
BD = 20cm. Độ dài cạnh BC là:
-
A.
10 cm
-
B.
12cm
-
C.
15cm
-
D.
9cm
Bài 14 :
Cho \(\Delta MNP \backsim \Delta EFH\) theo tỉ số k. Gọi \(M{M'},E{E'}\) lần lượt là hai trung tuyến của \(\Delta MNP\) và \(\Delta EFH\) . Khi đó ta chứng minh được:
-
A.
\(\frac{{E{E'}}}{{M{M'}}} = k\)
-
B.
\(\frac{{M{M '}}}{{E{E '}}} = k\)
-
C.
\(\frac{{M{M '}}}{{E{E '}}} = {k^2}\)
-
D.
\(\frac{{E{E '}}}{{M{M '}}} = {k^2}\)
Bài 15 :
Cho hình vẽ dưới đây, tính giá trị của x
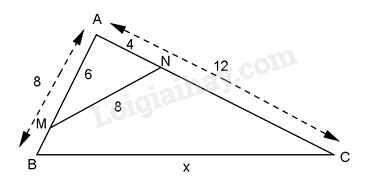
-
A.
x = 16
-
B.
x = 4
-
C.
x =10
-
D.
x = 14
Bài 16 :
Cho tam giác nhọn ABC có \(\hat C = {60^0}\) . Vẽ hình bình hành ABCD. Gọi AH, AK theo thứ tự là các đường cao của tam giác ABC, ACD. Tính số đo góc AKH.
-
A.
\({30^0}\)
-
B.
\({60^0}\)
-
C.
\({45^0}\)
-
D.
\({50^0}\)
Bài 17 :
Cho tam giác ABC có AB = 9cm, AC = 16cm, BC = 20cm. Hỏi góc B bằng bao nhiêu lần góc A?
-
A.
\(\hat B = \frac{{\hat A}}{3}\)
-
B.
\(\hat B = \frac{2}{3}\hat A\)
-
C.
\(\hat B = \frac{{\hat A}}{2}\)
-
D.
\(\hat B = \hat A\)
Bài 18 :
Cho hình thoi ABCD cạnh a, có \(\hat A = {60^0}\) . Một đường thẳng bất kì đi qua C cắt tia đối của các tia BA, DA tương ứng ở M, N. Gọi K là giao điểm của BN và DM. Tính \(\widehat {BKD}\) .
-
A.
\(\widehat {BKD} = {60^0}\)
-
B.
\(\widehat {BKD} = {100^0}\)
-
C.
\(\widehat {BKD} = {120^0}\)
-
D.
\(\widehat {BKD} = {115^0}\)
Bài 19 :
Hãy chỉ ra cặp tam giác đồng dạng trong các tam giác sau
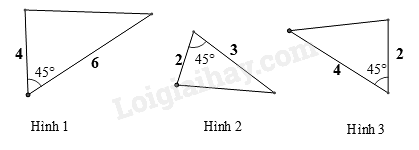
-
A.
Hình 1 và Hình 2.
-
B.
Hình 2 và Hình 3.
-
C.
Hình 1 và Hình 3.
-
D.
Đáp án A và C đều đúng.
Bài 20 :
Những cặp tam giác nào trong hình 9.17 là đồng dạng? (Các kích thước được tính theo đơn vị centimét). Viết đúng kí hiệu đồng dạng.

Bài 21 :
Cho ΔA'B'C' ∽ ΔABC. Trên tia đối của các tia CB, C'B' lần lượt lấy các điểm M, M' sao cho \(\frac{{MC}}{{MB}} = \frac{{M'C'}}{{M'B'}}\). Chứng minh rằng ΔA'B'M' ∽ ΔABM
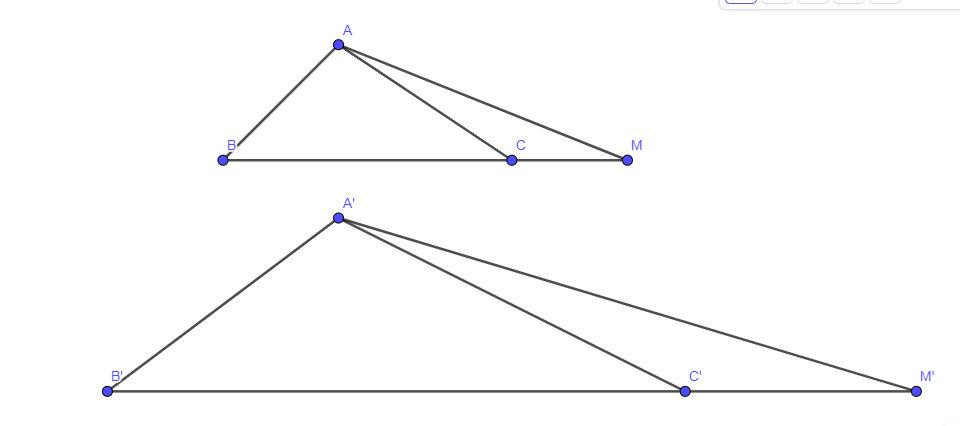
Bài 22 :
Bạn Lan nhận xét rằng nếu tam giác ABC và tam giác A’B’C’ có \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\) và \(\widehat {B'} = \widehat B\) thì chúng đồng dạng. Theo em bạn Lan nhận xét đúng không vì sao?
Gợi ý. Khi góc ACB tù, lấy điểm M trên tia BC sao cho \( \Delta AMC \) cân (H.9.19) rồi xét xem trong hai tam giác ABC và ABM, tam giác nào đồng dạng với tam giác A'B'C'.
Bài 23 :
Cho tam giác \(ADE\) và tam giác \(ACF\) có các kích thước như trong Hình 8. Chứng minh rằng \(\Delta ADE\backsim\Delta ACF\).
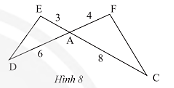
Bài 24 :
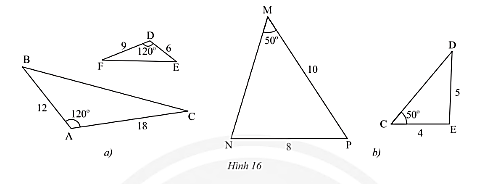
Xét xem cặp tam giác nào trong Hình 16a,16b đồng dạng?
Bài 25 :
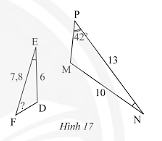
Trong Hình 17, cho biết \(DE = 6cm,EF = 7,8cm,NP = 13cm,NM = 10cm,\widehat E = \widehat N\) và \(\widehat P = 42^\circ \). Tính \(\widehat F\).
Bài 26 :
a) Cho tam giác \(ABC\) có \(AB = 12cm,AC = 15cm,BC = 18cm\). Trên cạnh \(AB\), lấy điểm \(E\) sao cho \(AE = 10cm\). Trên cạnh \(AC\), lấy điểm \(F\) sao cho \(AF = 8cm\) (hình 18a). Tính độ dài đoan thẳng \(EF\).
b) Trong Hình 18b, cho biết \(FD = FC,BC = 9dm,DE = 12dm,AC = 15dm,MD = 20dm.\)
Chứng minh rằng \(\Delta ABC\backsim\Delta MED\).

Bài 27 :
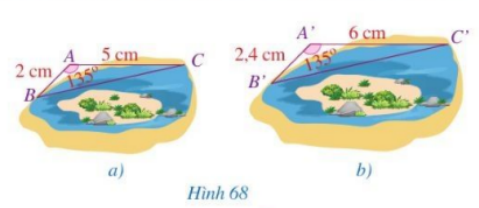
Quan sát hình 68 và so sánh:
a) Các tỉ số \(\frac{{A'B'}}{{AB}}\) và \(\frac{{A'C'}}{{AC}}\)
b) Các góc \(\widehat A\) và \(\widehat {A'}\)
Bài 28 :
Cho hai tam giác ABC và A’B’C’ thỏa mãn \(AB = 2,AC = 3,A'B' = 6,A'C' = 9\) và \(\widehat A = \widehat {A'}\). Chứng minh \(\widehat B = \widehat {B'},\,\,\widehat C = \widehat {C'}\).
Bài 29 :
Cho góc \(xOy\). Trên tia Ox lấy các điểm A, B sao cho \(OA = 2cm,\,\,OB = 9cm\). Trên tia Oy lấy các điểm M, N sao cho \(OM = 3cm,\,\,ON = 6cm\). ChỨNG minh \(\widehat {OBM} = \widehat {ONA}\).
Bài 30 :
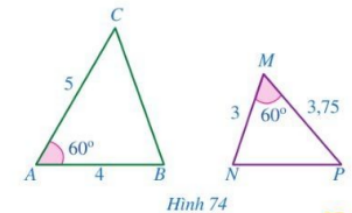
Cho Hình 74.
a) Chứng minh \(\Delta ABC \backsim \Delta MNP\)
b) Góc nào của tam giác MNP bằng góc B?
c) Góc nào của tam giác ABC bằng góc P?


















Danh sách bình luận