Bảng sau đây thống kê kết quả khảo sát số người thích một bộ phim mới tại 5 quận A, B, C, D, E của thành phố X

a) Chọn ngẫu nhiên một người ở quận C. Ước lượng xác suất của biến cố:
A: "Người được chọn thích bộ phim đó"
b) Chọn ngẫu nhiên một người ở quận E. Ước lượng xác suất của biến cố:
B: "Người được chọn không thích bộ phim đó"
c) Chọn ngẫu nhiên 600 người ở thành phố X. Ước lượng trong đó có bao nhiêu người thích bộ phim đó
d) Chọn ngẫu nhiên 500 người nữ ở thành phố X. Ước lượng trong đó có bao nhiêu người thích bộ phim đó?
Tính xác suất của biến cố A, B từ đó ước lượng số người thích bộ phim đó.
a) Có tổng 101 người ở quận C tham gia khảo sát => Có 101 kết quả có thể của hành động trên
Có 26 người thích bộ phim đó => Có 26 kết quả thuận lợi cho biến cố A . Vậy \(P(A) = \frac{{26}}{{101}} \approx 0,257\)
b) Có 79 người ở quận E tham gia khảo sát
Có 11 người thích bộ phim => Có 68 người không thích => Có 68 kết quả thuận lợi cho biến cố B. Vậy \(P(B) = \frac{{68}}{{79}} \approx 0,86\)
c) Có tổng 415 người của thành phố X tham gia khảo sát. Có 92 người thích bộ phim => Xác suất của biến cố "Người được chọn thích bộ phim trong 415 người của thành phố X" là: \(\frac{{92}}{{415}}\)
Vậy trong 600 người, số lượng người thích bộ phim khoảng \(\frac{{92.600}}{{415}}\) ≈ 133 (người)
d) Có tổng 214 người nữ của thành phố X tham gia khảo sát trong đó có 44 người thích bộ phim => Xác suất của biến cố "Người nữ được chọn thích bộ phim trong 214 người nữ của thành phố X" là: \(\frac{{44}}{{214}}\)
Vậy chọn ngẫu nhiên 500 người nữ, số lượng người nữ thích bộ phim khoảng \(\frac{{44.500}}{{214}}\) ≈ 103 (người)

Các bài tập cùng chuyên đề
Bài 1 :
Khi nói về xác suất thực nghiệm và xác suất. Chọn câu trả lời sai
-
A.
Xác suất thực nghiệm được dùng để ước lượng xác suất của một biến cố.
-
B.
Xác suất thực nghiệm và xác suất của cùng một sự kiện hay biến cố bằng nhau.
-
C.
Xác suất thực nghiệm được dùng để ước lượng xác suất của một biến cố khi các kết quả có thể của một hành động hay sự kiện không đồng khả năng.
-
D.
Xác suất thực nghiệm được dùng để ước lượng xác suất của một biến cố khi các kết quả có thể của một hành động hay sự kiện đồng khả năng.
Bài 2 :
Trong trò chơi gieo xúc xắc, khi số lần gieo xúc xắc ngày càng lớn thì xác xuất thực nghiệm của biến cố: “Mặt xuất hiện của xúc xắc là mặt k chấm” ngày càng gần với số thực nào?
-
A.
0,5.
-
B.
\(\frac{1}{6}\) .
-
C.
\(\frac{k}{6}\) .
-
D.
\(\frac{5}{6}\) .
Bài 5 :
Theo thống kê của một bệnh viện Sản, cứ 200 trẻ sơ sinh chào đời thì có 120 bé trai. Hãy ước lượng xem nếu có 1000 trẻ sơ sinh chào đời thì có bao nhiêu bé trai?
-
A.
400 bé.
-
B.
600 bé.
-
C.
800 bé.
-
D.
500 bé.
Bài 6 :
Nhà bếp của công nhân một xí nghiệp mua 40 khay trứng gà. Kiểm tra thì thấy ba khay, mỗi khay có ít nhất một quả trứng bị vỡ. Trong một tháng nhà bếp này mua 360 khay trứng. Hãy dự đoán xem có bao nhiêu khay có trứng vỡ?
-
A.
3 khay.
-
B.
27 khay.
-
C.
120 khay.
-
D.
9 khay.
Bài 7 :
Ở rạp chiếu phim, người ta thống kê được xác suất số người đặt vé trước đều có mặt là 0,95. Trong ngày công chiếu phim, có 240 người đặt chỗ trước. Hãy ước lượng số người đặt vé trước nhưng không đến.
-
A.
238 người.
-
B.
252 người.
-
C.
12 người.
-
D.
228 người.
Bài 8 :
Bạn An bỏ một số thẻ gỗ có đánh các số tự nhiên ( kích thước và khối lượng như nhau) vào trong một chiếc hộp. An lấy ra ngẫu nhiên một tấm thẻ, xem số rồi trả lại hộp. Lặp lại hành động đó 60 lần, An thấy có 24 lần lấy được thẻ ghi số chẵn. Biết trong hộp có 18 thẻ ghi số lẻ. Kết quả nào gần đúng với tổng số thẻ có trong hộp?
-
A.
30 thẻ.
-
B.
45 thẻ.
-
C.
12 thẻ.
-
D.
24 thẻ .
Bài 9 :
Trong hộp có một số bút xanh, một số bút vàng và một số bút đỏ, biết số bút xanh gấp đôi số bút đỏ. Lấy ngẫu nhiên 1 bút từ hộp, xem màu gì rồi trả lại. Lặp lại hoạt động trên 100 lần ta được kết quả như sau:

Biết số bút vàng là 20 cái. Ước lượng tổng số bút.
-
A.
60 cái bút.
-
B.
50 cái bút.
-
C.
40 cái bút.
-
D.
80 cái bút.
Bài 10 :
Bạn An có một số cái kẹo, trong đó 6 cái kẹo vị dâu. Mẹ An cho bạn thêm một số kẹo vị khác đúng bằng số kẹo An có hiện tại, vì thế xác suất chọn được kẹo vị dâu An có bây giờ là \(\frac{1}{4}\) . Tính số kẹo ban đầu của An.
-
A.
12 cái.
-
B.
24 cái.
-
C.
6 cái.
-
D.
48 cái.
Bài 11 :
Hình 8.4 là cảnh tắc đường ở đường Nguyễn Trãi (Hà Nội) vào giờ cao điểm buổi sáng, từ khoảng 7 giờ 30 phút đến 8 giờ. Giả sử camera quan sát đường Nguyễn Trãi trong 365 ngày ghi nhận được 217 ngày tắc đường vào giờ cao điểm buổi sáng. Từ só liệu thống kê đó, hãy ước lượng xác suất của biến cố E: "Tắc đường vào giờ cao điểm buổi sáng ở đường Nguyễn Trãi"
Bài 12 :
Trong 240 000 trẻ sơ sinh chào đời người ta thấy có 123 120 bé trai. Hãy ước lượng xác suất của biến cố "Trẻ sơ sinh là bé gái"
Bài 13 :
Thống kê điểm kiểm tra cuối năm môn Toán của một nhóm 100 học sinh lớp 8 được chọn ngẫu nhiên tại ba lớp của trường Trung học cơ sở X, thu được kết quả như bảng sau:
|
Điểm |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Số hs |
7 |
9 |
11 |
11 |
12 |
12 |
13 |
9 |
8 |
8 |
a) Chọn ngẫu nhiên một học sinh của trường X. Hãy tính xác suất thực nghiệm của các biến cố sau:
A: "Học sinh đó có điểm nhỏ hơn hoặc bằng 5"
B: "Học sinh đó có điểm từ 4 đến 9"
b) Hãy dự đoán trong nhóm 80 học sinh lớp 8 chọn ngẫu nhiên từ ba lớp khác của trường X:
Có bao nhiêu học sinh có số điểm không vượt quá 5 điểm?
Có bao nhiêu học sinh có số điểm từ 4 đến 9 điểm?
Bài 14 :
Thống kê về số ca nhiễm bệnh và số ca tử vong của bệnh SARS và bệnh EBOLA được kết quả như sau:
|
Bệnh |
Số người nhiễm |
Số người tử vong |
|
SARS( 11-2002 đến 7 – 2003) |
8 437 |
813 |
|
EBOLA (2014 – 2016) |
34 453 |
15 158 |
Căn cứ vào bảng thống kê trên, hãy ước lượng xác suất một người tử vong khi nhiễm bệnh SARS, bệnh EBOLA
Bài 15 :
Một nhà máy sản xuất máy điều hòa tiến hành kiểm tra chất lượng của 600 chiếc điều hòa được sản xuất và thấy có 5 chiếc bị lỗi. Trong một lô hàng có 1500 chiếc điều hòa, hãy dự đoán xem có khoảng bao nhiêu chiếc điều hòa không bị lỗi
Bài 16 :
Hai bạn Mai và Việt lần lượt thực hiện việc gieo đồng thời hai con xúc xắc và ở mỗi lần gieo sẽ nhận được số điểm bằng tổng số chấm xuất hiện trên hai con xúc xắc. Mai được gieo 100 lần và Việt được gieo 120 lần. Mai gieo trước và ghi lại kết quả của mình như sau:
|
Số điểm |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Số lần |
3 |
5 |
9 |
10 |
14 |
16 |
13 |
11 |
8 |
7 |
4 |
Trước khi Việt gieo, hãy dự đoán xem có bao nhiêu lần số điểm của Việt nhận được là:
a) Một số chẵn
b) Một số nguyên tố
c) Một số lớn hơn 7
Bài 17 :
Thống kê số vụ tai nạn giao thông trong hai tháng 8 và 9 của thành phố X được kết quả như bảng sau:
|
Số vụ tai nạn giao thông xảy ra trong môt ngày |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
≥8 |
|
Số ngày |
4 |
9 |
15 |
10 |
8 |
6 |
4 |
3 |
2 |
Từ bảng thống kê trên, hãy dự đoán xem trong ba tháng 10; 11; 12 tới tại thành phố X:
a) Có bao nhiêu ngày có nhiều nhất 3 vụ tai nạn giao thông
b) Có bao nhiêu ngày có ít nhất 5 vụ tai nạn giao thông
Bài 18 :
Hãy trả lời câu hỏi ở (trang 92)
Trước khi Hà tung một đồng xu cân đối và đồng chất 100 lần, Thọ dự đoán sẽ có trên 70 lần xuất hiện mặt sấp còn Thúy lại dự đoán sẽ có ít hơn 70 lần xuất hiện mặt sấp. Theo em, bạn nào có khả năng dự đoán cao hơn? Vì sao?
Bài 19 :
Một hộp chứa một số quả bóng xanh và bóng đỏ. Linh lấy ra ngẫu nhiên 1 quả bóng từ hộp, xem màu rồi trả bóng lại hộp. Lặp lại phép thử đó 200 lần, Linh thấy có 62 lần lấy được bóng xanh và 138 lần lấy được bóng đỏ.
a) Tính xác suất thực nghiệm của biến cố “Lấy được bóng xanh” sau 200 lần thử.
b) Biết số bóng xanh trong hộp là 20, hãy ước lượng số bóng đỏ trong hộp.
Bài 20 :
Xác suất nảy mầm của một loại hạt giống là 0,8. Người ta đem gieo 1000 hạt giống đó. Hãy ước lượng xem có khoảng bao nhiêu hạt trong số đó sẽ nảy mầm.
Bài 21 :
Ở một sân bay người ta nhận thấy với mỗi chuyến bay, xác suất tất cả mọi người đều có mặt để lên máy bay là 0,9. Trong một ngày, sân bay có 120 lượt máy bay cất cánh. Hãy ước lượng số chuyến bay trong ngày hôm đó có người mua vé nhưng không lên máy bay.
Bài 22 :
Một hộp chứa các viên bi màu trắng và đen có kích thước và khối lượng như nhau. Mai lấy ra ngẫu nhiên 1 viên bi từ hộp, xem màu rồi trả lại hộp. Lặp lại thử nghiệm đó 80 lần, Mai thấy có 24 lần lấy được viên bi màu trắng.
a) Hãy tính xác suất thực nghiệm của biến cố “Lấy được viên bi màu đen” sau 80 lần thử.
b) Biết tổng số bi trong hộp là 10. Hãy ước lượng xem trong hộp có khoảng bao nhiêu viên bi trắng.
Bài 23 :
Trong một cuộc điều tra, người ta phỏng vấn 300 người được lựa chọn ngẫu nhiên ở một khu dân cư thì thấy có 255 người ủng hộ việc tắt điện trong sự kiện Giờ Trái Đất. Hãy ước lượng xác suất của biến cố “Một người được lựa chọn ngẫu nhiên trong khu dân cư ủng hộ việc tắt đèn điện trong sự kiện Giờ Trái Đất”.
Bài 24 :
Thúy gieo một con xúc xắc cân đối 1000 lần. Số lần xuất hiện mặt 6 chấm trong 1000 lần gieo đó có khả năng lớn nhất thuộc vào tập hợp nào sau đây?
A. {0; 1; …; 100}.
B. {101; 102; …; 200}.
C. {201; 202; …; 300}.
C. {301; 302; … ; 400}.
Bài 25 :
Xuân bỏ một số viên bi xanh và đỏ có kích thước và khối lượng giống nhau vào túi. Mỗi lần Xuân lấy ra ngẫu nhiên 1 viên bi, xem màu của nó rồi trả lại túi. Lặp lại phép thử đó 100 lần, Xuân thấy có 40 lần mình lấy được bi đỏ. Biết rằng trong túi có 9 viên bi xanh, hãy ước lượng xem trong túi có bao nhiêu viên bi đỏ.
Bài 26 :
Một tấm bìa hình tròn được chia thành 6 phần bằng nhau như Hình 1. Bạn Thủy quay mũi tên và quan sát xem khi dừng lại mũi tên chỉ vào ô số mấy. Thủy ghi lại kết quả sau 120 lần thí nghiệm ở bảng sau:
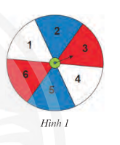

a) Tính xác suất thực nghiệm của biến cố “Mũi tên chỉ vào ô có màu trắng”.
b) Theo dự đoán, xác suất mũi tên chỉ vào mỗi ô có bằng nhau không?
c) Một người nhận định rằng xác suất mũi tên chỉ vào các ô màu xanh bằng xác suất mũi tên chỉ vào các ô màu trằng và bằng xác suất chỉ vào các ô màu đỏ. Theo em, kết quả thực nghiệm của bạn Thủy có phù hợp với nhận định đó không?
Bài 27 :
Trong trò chơi gieo xúc xắc, khi số lần gieo xúc xắc ngày càng lớn thì xác suất thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc có số chấm là số chẵn” ngày càng gần với số thực nào?
Bài 28 :
Một hộp có 10 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số ngày nguyên dương không vượt quá 10, hai thẻ khác nhau thì ghi hai số khác nhau.
Lấy ngẫu nhiên một chiếc thẻ từ trong hộp, ghi lại số của thẻ lấy ra và bỏ lại thẻ đó vào hộp.
a) Sau 30 lần rút thẻ liên tiếp, tính xác suất thực nghiệm của mỗi biến cố sau:
- “Thẻ rút ra ghi số 1”;
- “Thẻ rút ra ghi số 5”;
- “Thẻ rút ra ghi số 10”.
b) Nêu mối liên hệ giữa xác suất thực nghiệm của biến cố “Thẻ rút ra ghi số chia hết cho 3” với xác suất của biến cố đó khi số lần rút thẻ ngày càng lớn.
Bài 29 :
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số nguyên dương không vượt quá 5, hai thẻ khác nhau thì ghi hai số khác nhau. Lấy ngẫu nhiên một chiếc thẻ từ trong hộp, ghi lại số của thẻ lấy ra và bỏ lại thẻ đó vào hộp.
a) Sau 40 lần lấy thẻ liên tiếp, hãy tính xác suất thực nghiệm của các biến cố sau "Thẻ lấy ra ghi số chẵn" và "Thẻ lấy ra ghi số lẻ".
b) Tính xác suất của các biến cố "Thẻ lấy ra ghi số chẵn" và "Thẻ lấy ra ghi số lẻ".
c) Nêu mối liên hệ giữa xác suất thực nghiệm của mỗi biến cố "Thẻ lấy ra ghi số chẵn" và "Thẻ lấy ra ghi số lẻ" với xác suất của mỗi biến cố đó khi số lần lấy thẻ ngày càng lớn.
Bài 30 :
a) Gieo con xúc sắc cân đối và đồng chất có \(6\) mặt. Tính xác suất của \(6\) biến cố \({E_1},{E_2},{E_3},{E_4},{E_5},{E_6}\) trong đó \({E_i}\left( {1 \le i \le 6} \right)\) là nhận được mặt \(i\) chấm”.
b) Bảng 7.10a ghi lại kết quả mà Đào thu được trong \(100\) lần gieo xúc xắc.

Tính xác suất thực nghiệm của các biến cố \({E_1},{E_2},{E_3},{E_4},{E_5},{E_6}\) trong thí nghiệm của Đào.
c) Bảng 7.10b ghi lại kết quả mà \(9\) bạn trong tổ của Lan thu được sau \(1800\) lần gieo xúc xắc (mỗi bạn gieo \(200\) lần, ghi lại kết quả, sau đó tổng hợp dữ liệu trong Bảng 7.10b).

Tính xác suất thực nghiệm của các biến cố \({E_1},{E_2},{E_3},{E_4},{E_5},{E_6}\) trong thí nghiệm của tổ bạn Lan.
d) Với mỗi biến cố \({E_i}\left( {1 \le i \le 6} \right),\) có nhận xét gì về kết quả tìm được ở các câu a,b,c?


















Danh sách bình luận