Tính chiều dài đường trượt AC trong hình vẽ bên (kết quả làm tròn hàng phần mười).
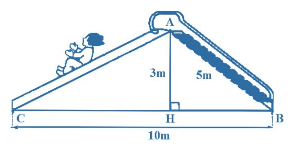

Sử dụng định lý Pythagore tính lần lượt cac cạnh HB, AC
Áp dụng định lí Pythagore trong tam giác AHB vuông tại H ta có:
\(A{B^2} = A{H^2} + H{B^2}\)
Suy ra \(H{B^2} = A{B^2} - A{H^2} = {5^2} - {3^2} = 25 - 9 = 16\)
Do đó \(HB = \sqrt {16} = 4\,cm\), nên \(CH = BC - HB = 10 - 4 = 6\,cm\).
Áp dụng định lí Pythagore trong tam giác AHC vuông tại H ta có:
\(A{C^2} = A{H^2} + H{C^2} = {3^2} + {6^2} = 9 + 36 = 45\)
Suy ra \(AC = \sqrt {45} \approx 6,7\,m\)
Vậy chiều dài đường trượt AC là \(6,7\,m\).

Các bài tập cùng chuyên đề
Bài 1 :
Tính các độ dài \(PN\) và \(BC\) trong Hình 9.
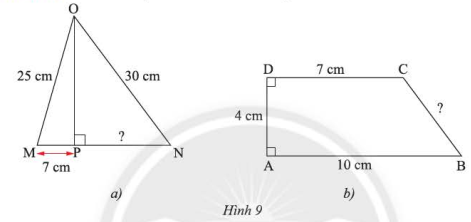
Bài 2 :
Tính chiều dài cần cẩu \(AB\) trong Hình 10.
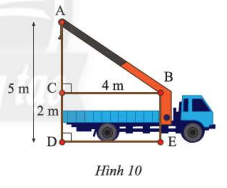
Bài 3 :
Tính độ cao của con diều so với mặt đất (Hình 11)
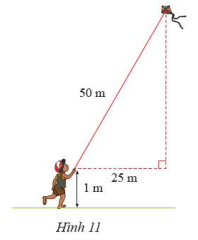
Bài 4 :
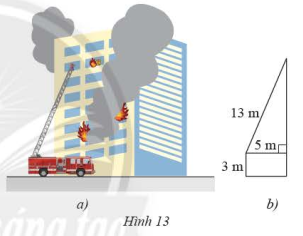
Cho biết thang của một xe máy cứu hỏa có chiều dài \(13\)m, chân thang cách mặt đất \(3\)m và cách tường của toàn nhà \(5\)m. Tính chiều cao mà thang có thể vươn tới.
Bài 5 :
Một con thuyền đang neo ở một điểm cách chân tháp hải đăng \(180\)m. Cho biết tháp hải đăng cao \(25\)m. Hãy tính khoảng cách từ thuyền đến đỉnh tháp hải đăng.

Bài 6 :
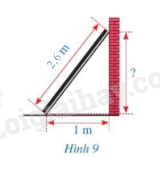
Hình 9 mô tả một thanh gỗ dài 2,6 m dựa vào một bức tường thẳng đứng. Chân thanh gỗ cách mép tường một khoảng là 1 m. Khoảng cách từ điểm thanh gỗ chạm vào tường đến mặt đất là bao nhiêu mét?
Bài 7 :
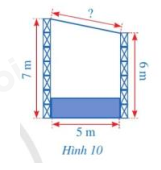
Hình 10 mô tả mặt cắt đứng của một sân khấu ngoài trời có mái che. Chiều cao của khung phía trước khoảng 7 m, chiều cao của khung phía sau là 6 m, hai khung cách nhau một khoảng 5 m. Chiều dài của mái che sân khấu đó là bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)
Bài 8 :
Hình 72 mô tả một cây cao 4m. Biết rằng khi trời nắng, cây đổ bóng trên mặt đất, điểm xa nhất của bóng cây cách gốc cây một khoảng là 3 m. Tính khoảng cách từ điểm xa nhất của bóng cây đến đỉnh của cây.
Bài 9 :
Màn hình một chiếc ti vi có dạng hình chữ nhật với kích thước màn hình ti vi được tính bằng độ dài đường chéo của màn hình (đơn vị: inch, trong đó 1 inch = 2, 54 cm). Người ta đưa ra công thức tính khoảng cách an toàn khi xem ti vi để giúp khách hàng lựa chọn được chiếc ti vi phù hợp với căn phòng của mình như sau:
Khoảng cách tối thiểu = 5, 08 . d (cm)
Khoảng cách tối đa = 7, 62 . d (cm)
Trong đó, d là kích thước màn hình ti vi tính theo inch.
Với một chiếc ti vi có chiều dài màn hình 74, 7 cm, chiều rộng màn hình 32 cm;
a) Kích thước màn hình của ti vi đó là bao nhiêu inch (làm tròn kết quả đến hàng đơn vị)?
b) Khoảng cách tối thiểu và khoảng cách tối đa để xem chiếc ti vi đó là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
Bài 10 :
Tính khoảng cách x từ đầu thang đến chân tường (Hình 9).

Bài 11 :
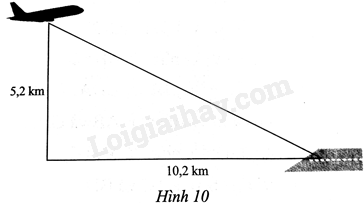
Một máy bay đang ở độ cao 5,2km. Khoảng cách từ hình chiếu vuông góc của máy bay xuống mặt đất đến vị trí A của sân bay là 10,2km (Hình 10). Tính khoảng cách từ vị trí máy bay đến vị trí A của sân bay.
Bài 12 :
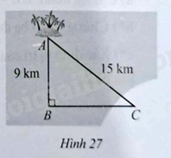
Một công ti dự định làm một đường ống dẫn từ một nhà máu ở địa điểm \(C\) trên bờ đến một địa điểm \(B\) trên biển. Khoảng cách giữa địa điểm \(A\) trên đảo với địa điểm \(B\), địa điểm \(C\) lần lượt là \(9km\), \(15km\); \(AB\) vuông góc với \(BC\) (minh họa ở Hình 27). Giá làm 1 km đường ống là 5 000 đô la Mỹ. Hỏi chi phí làm đường ống từ địa điểm \(C\) đến địa điểm \(B\) là bao nhiêu đồng? Biết 1 đô la Mỹ bằng 23 635 đồng.
Bài 13 :
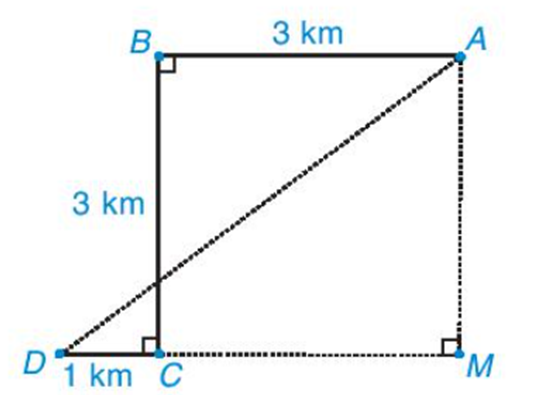
Để đón được một người khách, một xe taxi xuất phát từ vị trí điểm A, chạy dọc một con phố dài 3km đến điểm B thì rẽ vuông góc sang trái, chạy được 3km đến điểm C thì tài xế cho xe rẽ vuông góc sang phải, chạy 1km nữa thì gặp người khách tại điểm D (H.9.38). Hỏi lúc đầu, khoảng cách từ chỗ người lái xe đến người khác là bao nhiêu kilômét.
Bài 14 :
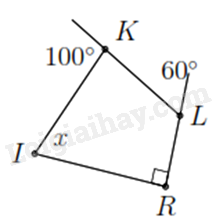
a) Tìm \(x\) trong hình vẽ bên.
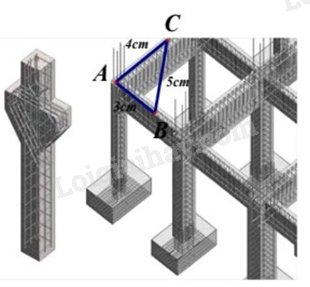
b) Khi xây móng nhà, để kiểm tra xem 2 phần móng có vuông góc với nhau hay không, người thợ xây thường lấy \(AB = 3cm,AC = 4cm\) (A là điểm chung của hai phần móng nhà hay còn gọi là góc nhà), rồi đo đoạn \(BC = 5cm\) thì hai phần móng đó vuông góc với nhau. Hãy giải thích vì sao?
Bài 15 :
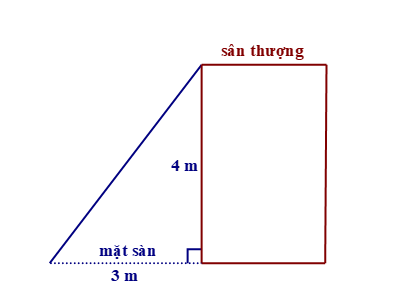
Bác thợ muốn xây một cầu thang bắc từ mặt sàn lên sân thượng. Biết rằng bức tường từ sàn lên sân thượng cao \(4\,m\), chân cầu thang cách bức tường \(3\,m\). Khi đó, chiều dài của cầu thang là:
-
A.
\(4\,m\);
-
B.
\(5\,m\);
-
C.
\(6\,m\);
-
D.
\(7\,m\).
Bài 16 :
Một chiếc cầu thang có các kích thước như hình vẽ sau:
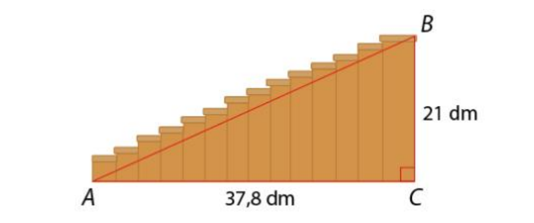
Tính độ dài đoạn thẳng \(AB\).
-
A.
\(AB \approx 43,2\,dm\);
-
B.
\(AB \approx 43,3\,dm\)
-
C.
\(AB \approx 44,2\,dm\)
-
D.
\(AB \approx 44,3\,dm\)
Bài 17 :
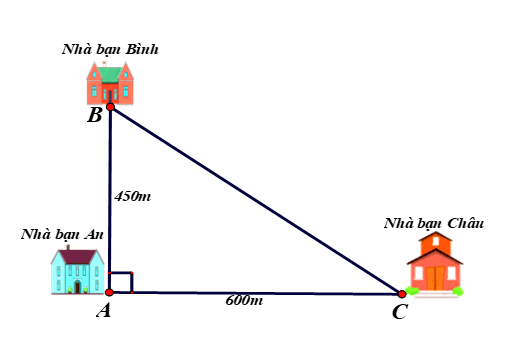
Nhà bạn An (vị trí \(A\) trên hình vẽ) cách nhà bạn Châu (vị trí \(C\) trên hình vẽ) \(600\,m\) và cách nhà bạn Bình (vị trí \(B\) trên hình vẽ) \(450\,m\). Biết rằng 3 vị trí: nhà An, nhà Bình và nhà Châu là 3 đỉnh của một tam giác vuông (xem hình vẽ). Hãy tính khoảng cách từ nhà Bình đến nhà Châu.
-
A.
\(300\, m\);
-
B.
\(450\, m\);
-
C.
\(600\, m\);
-
D.
\(750\, m\).
Bài 18 :
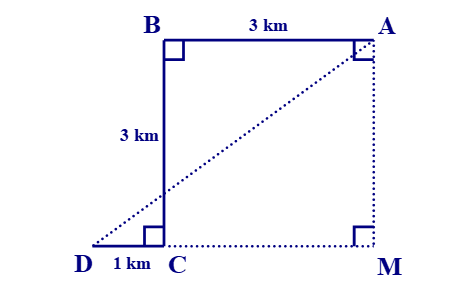
Để đón được một người khách, một xe taxi xuất phát từ vị trí điểm \(A\), chạy dọc một con phố dài \(3\, km\) đến điểm \(B\) thì rẽ vuông góc sang trái, chạy được \(3\,km\) đến điểm \(C\) thì tài xế cho xe rẽ vuông góc sang phải, chạy \(1\,km\) nữa thì gặp người khách tại điểm \(D\). Hỏi lúc đầu, khoảng cách từ chỗ người lái xe đến người khách là bao nhiêu ki-lô-mét?
-
A.
\(5\, km\);
-
B.
\(5\, m\);
-
C.
\(3\, km\);
-
D.
\(3\, m\).
Bài 19 :
Cho hình vẽ:
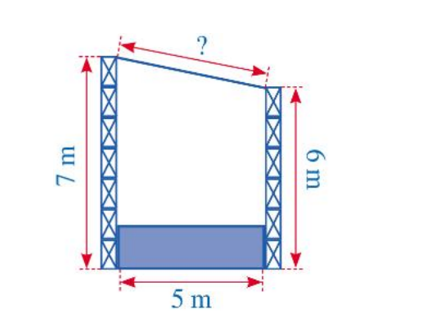
Hình vẽ trên mô tả mặt cắt đứng của một sân khấu ngoài trời có mái che. Chiều cao của khung phía trước khoảng \(7\,m\), chiều cao của khung phía sau là \(6\,m\), hai khung cách nhau một khoảng \(5\, m\). Chiều dài của mái che sân khấu khoảng … mét.
Số thích hợp để điền vào chỗ chấm là:
-
A.
\(5,0\);
-
B.
\(5,1\);
-
C.
\(5,2\);
-
D.
\(5,3\).
Bài 20 :
Hình dưới đây mô tả một cánh buồm có dạng tam giác vuông, được buộc vào cột buồm thẳng đứng, với độ dài hai cạnh góc vuông là \(12\,m\) và \(5\,m\).
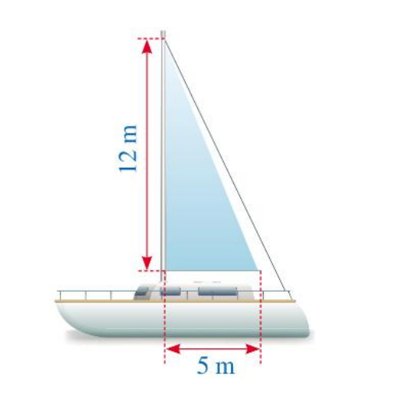
Chu vi của cánh buồm là:
-
A.
\(13\, m\);
-
B.
\(15\, m\);
-
C.
\(40\, m\);
-
D.
\(30\, m\).
Bài 21 :
Cho hình vẽ:

Hình vẽ trên mô tả mặt cắt dọc phần nổi trên mặt nước của một chiếc tàu thuỷ. Tính chu vi mặt cắt dọc phần nổi trên mặt nước của chiếc tàu thuỷ đó (làm tròn kết quả đến hàng phần mười).
-
A.
\(101,4\, m\);
-
B.
\(102,4\, m\);
-
C.
\(101,3\, m\);
-
D.
\(102,5\, m\).
Bài 22 :
Để chuyển hàng hoá từ thùng xe tải xuống cửa nhà kho, người ta dùng một tấm ván để tạo ra một “mặt phẳng nghiêng” giúp người vận chuyển giảm hao phí sức lực. Biết khoảng cách từ đầu tấm ván đặt ở thùng xe đến mặt đất là BA = 1,2m và tấm ván có chiều dài BC = 2m. Hỏi xe phải đậu cách cửa kho bao nhiêu mét để chân tấm ván (điểm C) vừa chạm đến cửa kho?
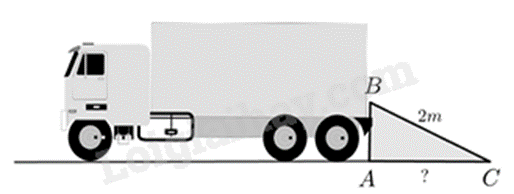
Bài 23 :
Cho tam giác ABC vuông tại A có AB = 16 cm, AC = 12 cm. Kẻ đường phân giác BD (D thuộc AC). Tính độ dài các đoạn thẳng CD và AD.
Bài 24 :
Một con thuyền đang neo ở một điểm cách chân tháp hải đăng 180m. Biết tháp hải đăng cao \(25\;{\rm{m}}\). Khoảng cách từ thuyền đến đỉnh tháp hải đăng bằng (làm tròn kết quả đến hàng đơn vị):

Bài 25 :
Ngọn hải đăng Lý Sơn (thuộc tỉnh Quảng Ngãi) cao 45m. Một con tàu đậu cách chân ngọn hải đăng 60m. Khoảng cách từ tàu đến đỉnh ngọn hải đăng là
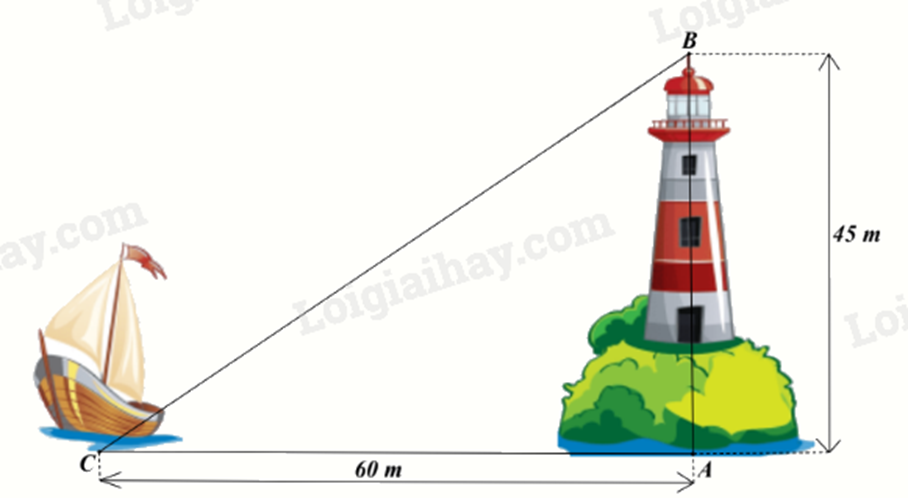
-
A.
75m.
-
B.
105m.
-
C.
85m.
-
D.
55m.
Bài 26 :
Một chiếc ti vi 24 inch có nghĩa là đường chéo màn hình của nó có độ dài là 24 inch (inch: đơn vị đo độ dài sử dụng ở nước Anh và một số nước khác, 1 inch \( \approx \) 2,54cm). Biết một ti vi màn hình phẳng có chiều dài, chiều rộng của màn hình lần lượt là 14,8 inch và 11,8 inch thì tivi đó thuộc loại bao nhiêu inch? (làm tròn đến chữ số thập phân thứ nhất)

Bài 27 :
Để đón một người khách, xe taxi xuất phát từ vị trí điểm A, chạy dọc một con phố dài 3 km đến điểm B thì rẽ vuông góc sang trái, chạy 3 km đến điểm C thì tài xế cho xe rẽ vuông góc sang phải, chạy 1 km nữa thì gặp vị khách tại điểm D (như hình vẽ).
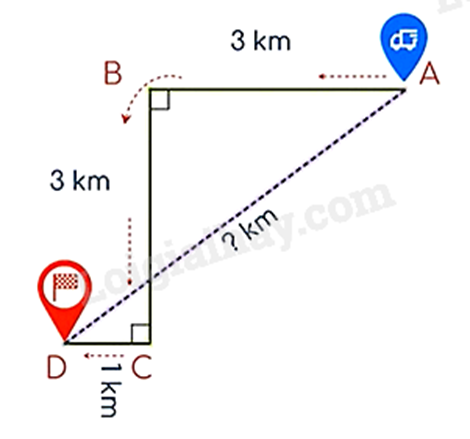
Hỏi lúc đầu khoảng cách từ chỗ người lái xe đến người khách là bao nhiêu kilômét?



















Danh sách bình luận