Trong không gian \(Oxyz\), cho điểm \({M_0}\) cố định và vectơ \(\vec a\) khác \(\vec 0\). Có bao nhiêu đường thẳng \(d\) đi qua \({M_0}\) và song song hoặc trùng với giá của \(\vec a\)?
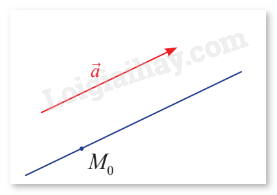
Trong không gian, qua một điểm không nằm trên một đường thẳng, có duy nhất một đường thẳng đi qua điểm và song song với đường thẳng đó.
Nếu điểm \({M_0}\) nằm trên giá của vectơ \(\vec a\), thì đường thẳng đó là đường thẳng duy nhất cần tìm.
Nếu điểm \({M_0}\) không nằm trên giá của vectơ \(\vec a\), do trong không gian, qua một điểm không nằm trên một đường thẳng, có duy nhất một đường thẳng đi qua điểm và song song với đường thẳng đó, nên tồn tại duy nhất một đường thẳng đi qua \({M_0}\) và song song với giá của vectơ \(\vec a\).
Như vậy, có duy nhất một đường thẳng \(d\) đi qua \({M_0}\) và song song hoặc trùng với giá của \(\vec a.\)
Các bài tập cùng chuyên đề
Trong không gian Oxyz, một vật thể chuyển động với vectơ vận tốc không đổi \(\overrightarrow u = \left( {a;b;c} \right) \ne \overrightarrow 0 \) và xuất phát từ điểm \(A\left( {{x_0};{y_0};{z_0}} \right)\) (H.5.26).
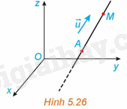
a) Hỏi vật thể chuyển động trên đường thẳng nào (chỉ ra điểm mà nó đi qua và vectơ chỉ phương của đường thẳng đó)?
b) Giả sử tại thời điểm t \(\left( {t > 0} \right)\) tính từ khi xuất phát, vật thể ở vị trí \(M\left( {x;{\rm{ }}y;{\rm{ }}z} \right).\) Tính x, y, z theo a, b, c, \({x_0};{y_0};{z_0}\) và t.
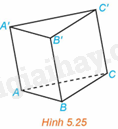
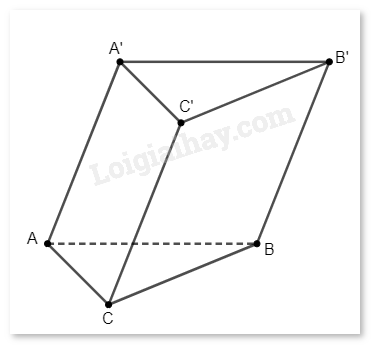
Cho hình lăng trụ ABC. A’B’C’ (H.5.25). Trong các vectơ có điểm đầu và điểm cuối đều là đỉnh của hình lăng trụ, những vectơ nào là vectơ chỉ phương của đường thẳng AB?
Trong không gian, cho điểm M và vectơ \(\overrightarrow u \) khác vectơ- không. Khẳng định nào trong hai khẳng định sau là đúng?
a) Có duy nhất đường thẳng đi qua M và vuông góc với giá của \(\overrightarrow u \).
b) Có duy nhất đường thẳng đi qua M và song song hoặc trùng với giá của \(\overrightarrow u \).
Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) tương ứng có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {{a_1};{b_1};{c_1}} \right),\overrightarrow {{u_2}} = \left( {{a_2};{b_2};{c_2}} \right)\).
a) Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) vuông góc với nhau khi và chỉ khi giá của \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) có mối quan hệ gì?
b) Tìm điều kiện đối với \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) để \({\Delta _1}\) và \({\Delta _2}\) vuông góc với nhau.
Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) lần lượt đi qua các điểm \({A_1}\left( {{x_1};{y_1};{z_1}} \right),{A_2}\left( {{x_2};{y_2};{z_2}} \right)\) và tương ứng có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {{a_1};{b_1};{c_1}} \right),\overrightarrow {{u_2}} = \left( {{a_2};{b_2};{c_2}} \right)\). (H.5.29).
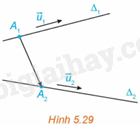
a) Tìm điều kiện đối với \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) để \({\Delta _1}\) và \({\Delta _2}\) song song hoặc trùng nhau.
b) Giả sử \(\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \) và \(\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = 0\) thì \({\Delta _1}\) và \({\Delta _2}\) có cắt nhau hay không?
c) Giả sử \(\overrightarrow {{A_1}{A_2}} .\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne 0\) thì \({\Delta _1}\) và \({\Delta _2}\) có chéo nhau hay không?
Trong không gian Oxyz, một viên đạn được bắn ra từ điểm \(A\left( {1;3;4} \right)\) và trong 3 giây, đầu đạn đi với vận tốc không đổi; vectơ vận tốc (trên giây) là \(\overrightarrow v = \left( {2;1;6} \right)\). Hỏi viên đạn trên có bắn trúng mục tiêu trong mỗi tình huống sau hay không?
a) Mục tiêu đặt tại điểm \(M\left( {7;\frac{7}{2};21} \right)\).
b) Mục tiêu đặt tại điểm \(N\left( { - 3;1; - 8} \right)\).
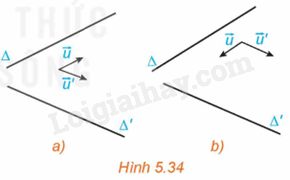
Trong không gian Oxyz, cho hai đường thẳng \(\Delta \) và \(\Delta '\) tương ứng có các vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right),\overrightarrow {u'} = \left( {a';b';c'} \right)\). (H.5.34).
a) Hãy tìm mối quan hệ giữa các góc \(\left( {\Delta ,\Delta '} \right)\) và \(\left( {\overrightarrow u ,\overrightarrow {u'} } \right)\).
b) Có nhận xét gì về mối quan hệ giữa \(\cos \left( {\Delta ,\Delta '} \right)\) và \(\left| {\cos \left( {\overrightarrow u ,\overrightarrow {u'} } \right)} \right|\)?
Trong không gian Oxyz, cho đường thẳng \(\Delta \) và mặt phẳng (P). Xét \(\overrightarrow u = \left( {a;b;c} \right)\) là một vectơ chỉ phương của \(\Delta \) và \(\overrightarrow n = \left( {A;B;C} \right)\) (với giá \(\Delta '\)) là một vectơ pháp tuyến của (P). (H.5.35)
a) Hãy tìm mối quan hệ giữa các góc \(\left( {\Delta ,\left( P \right)} \right)\) và \(\left( {\Delta ,\Delta '} \right)\).
b) Có nhận xét gì về mối quan hệ giữa \(\sin \left( {\Delta ,\Delta '} \right)\) và \(\left| {\cos \left( {\overrightarrow u ,\overrightarrow n } \right)} \right|\)?
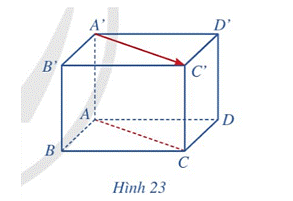
Cho hình hộp ABCD.A’B’C’D’ (Hình 23). Giá của vectơ \(\overrightarrow {A'C'} \) và đường thẳng AC có vị trí tương đối như thế nào?
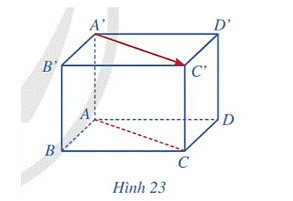
Trong Hình 23, vectơ \(\overrightarrow {B'D'} \) có là vectơ chỉ phương của đường thẳng BD hay không? Vì sao?
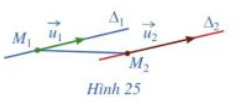
Cho hai đường thẳng phân biệt \({\Delta _1},{\Delta _2}\) lần lượt đi qua các điểm \({M_1},{M_2}\) và tương ứng có vectơ chỉ phương là \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) .
a) Giả sử \({\Delta _1}\) song song với \({\Delta _2}\) (Hình 25). Các cặp vectơ sau có cùng phương hay không: \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \); \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{M_1}{M_2}} \)?
b) Giả sử \({\Delta _1}\) và \({\Delta _2}\) cắt nhau (Hình 26). Hai vectơ \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) có cùng phương hay không? Ba vectơ \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) và \(\overrightarrow {{M_1}{M_2}} \) có đồng phẳng hay không?
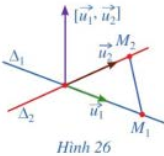
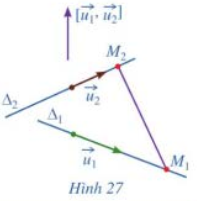
c) Giả sử \({\Delta _1}\) và \({\Delta _2}\) chéo nhau (Hình 27). Hai vectơ \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) có cùng phương hay không? Ba vectơ \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) và \(\overrightarrow {{M_1}{M_2}} \) có đồng phẳng hay không?
Trong không gian \(Oxyz\), cho hình lăng trụ tam giác \(ABC.A'B'C'\) với \(A\left( {1;2;1} \right)\), \(B\left( {7;5;3} \right)\), \(C\left( {4;2;0} \right)\), \(A'\left( {4;9;9} \right)\). Tìm toạ độ một vectơ chỉ phương của mỗi đường thẳng \(AB\), \(A'C'\) và \(BB'.\)
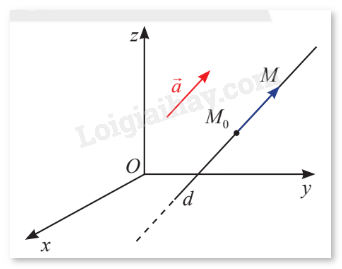
Trong không gian \(Oxyz\), cho đường thẳng \(d\) đi qua điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) cố định và có vectơ chỉ phương là \(\vec a = \left( {{a_1};{a_2};{a_3}} \right)\) khác \(\vec 0.\)
a) Giải thích tại sao ta có thể viết \(M \in d \Leftrightarrow \overrightarrow {{M_0}M} = t\vec a{\rm{ }}\left( {t \in \mathbb{R}} \right).\)
b) Với \(M\left( {x;y;z} \right)\) thuộc \(d\), hãy tính \(x\), \(y\), \(z\) theo \({x_0}\), \({y_0}\), \({z_0}\) và \({a_1}\), \({a_2}\), \({a_3}.\)
Cho đường thẳng \(d\) có phương trình tham số \(\left\{ \begin{array}{l}x = - 1 + 8t\\y = - 4t\\z = 3 + 12t\end{array} \right.\)
a) Tìm hai vectơ chỉ phương của \(d.\)
b) Tìm ba điểm trên \(d.\)
Viết phương trình tham số của đường thẳng \(d\) đi qua điểm \(A\left( {5;0; - 7} \right)\) và nhận \(\vec v = \left( {9;0; - 2} \right)\) làm vectơ chỉ phương. Đường thẳng \(d\) có đi qua điểm \(M\left( { - 4;0; - 5} \right)\) không?
Cho đường thẳng \(d:\frac{{x - 2}}{{ - 1}} = \frac{{y - 1}}{2} = \frac{{z + 3}}{1}\). Vectơ nào sau đây là một vectơ chỉ phương của \(d\)?
A. \(\overrightarrow {{u_1}} = \left( {2;1; - 3} \right)\)
B. \(\overrightarrow {{u_2}} = \left( { - 2; - 1;3} \right)\)
C. \(\overrightarrow {{u_3}} = \left( { - 1;2;1} \right)\)
D. \(\overrightarrow {{u_4}} = \left( { - 1;2; - 1} \right)\)
Vectơ nào sau đây là một vectơ chỉ phương của đường thẳng \(\left\{ \begin{array}{l}x = 7\\y = - 9 + t\\z = 16\end{array} \right.\)?
A. \(\overrightarrow {{u_1}} = \left( {7;9; - 16} \right)\).
B. \(\overrightarrow {{u_2}} = \left( {7; - 9;16} \right)\).
C. \(\overrightarrow {{u_3}} = \left( {0;1;0} \right)\).
D. \(\overrightarrow {{u_4}} = \left( { - 7;9; - 16} \right)\).
Vectơ nào sau đây là vectơ chỉ phương của đường thẳng \(d:\left\{ \begin{array}{l}x = 9 + 6t\\y = - 10 - 7t\\z = 11 + 8t\end{array} \right.\)?
A. \(\overrightarrow {{u_1}} = \left( {9; - 10;11} \right)\).
B. \(\overrightarrow {{u_2}} = \left( {6;7;8} \right)\).
C. \(\overrightarrow {{u_3}} = \left( {9;10;11} \right)\).
D. \(\overrightarrow {{u_4}} = \left( {6; - 7;8} \right)\).
Vectơ nào sau đây là vectơ chỉ phương của đường thẳng \(d:\left\{ \begin{array}{l}x = 8 - t\\y = 7\\z = - 6 + 9t\end{array} \right.\)?
A. \(\overrightarrow {{u_1}} = \left( { - 1;0;9} \right)\).
B. \(\overrightarrow {{u_2}} = \left( {8;7;6} \right)\).
C. \(\overrightarrow {{u_3}} = \left( {1;0;9} \right)\).
D. \(\overrightarrow {{u_4}} = \left( {8;7; - 6} \right)\).
Vectơ nào sau đây là vectơ chỉ phương của đường thẳng \(d:\frac{{x - 2}}{{15}} = \frac{{y + 9}}{{ - 10}} = \frac{{z - 7}}{5}\)?
A. \(\overrightarrow {{u_1}} = \left( {2; - 9;7} \right)\).
B. \(\overrightarrow {{u_2}} = \left( { - 2;9; - 7} \right)\).
C. \(\overrightarrow {{u_3}} = \left( {15;10;5} \right)\).
D. \(\overrightarrow {{u_4}} = \left( {3; - 2;1} \right)\).
Trong không gian Oxyz, một vectơ chỉ phương của đường thẳng có phương trình \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 3 - 2t\\z = - 2 + t\end{array} \right.\) là
A. \(\overrightarrow {{u_1}} = \left( {1;3; - 2} \right)\).
B. \(\overrightarrow {{u_2}} = \left( {2; - 2;0} \right)\)
C. \(\overrightarrow {{u_3}} = \left( {2;2;1} \right)\).
D. \(\overrightarrow {{u_4}} = \left( {4; - 2;1} \right)\).
Cho hình chóp S.ABCD với ABCD là hình bình hành. Gọi d là giao tuyến của hai mặt phẳng (SAB) và (SCD). Tìm các vectơ có điểm đầu và điểm cuối trong các điểm S, A, B, C, D đã cho và là vectơ chỉ phương của d.
Trong không gian Oxyz, cho đường thẳng \(d:\frac{{x - 1}}{2} = \frac{{y - 3}}{{ - 5}} = \frac{{z + 2}}{3}\). Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng d?
Trong không gian Oxyz, cho đường thẳng có phương trình d: \(\left\{ {\begin{array}{*{20}{c}}{x = 1 + t}\\{y = 2 - t}\\{z = 2 + 3t}\end{array}} \right.\). Mặt phẳng (P) vuông góc với d. Một vecto pháp tuyến của (P) là
Trong không gian Oxyz, cho hai điểm A(1;2;2), B(3;-2;0). Một vecto chỉ phương của đường thẳng AB là
Trong không gian Oxyz, cho đường thẳng d: \(\frac{{x - 3}}{1} = \frac{{y + 1}}{{ - 2}} = \frac{{z - 5}}{3}\). Vecto nào dưới đây là vecto chỉ phương của d?
Trong không gian Oxyz, cho đường thẳng \(\Delta :\frac{{x - 3}}{2} = \frac{{y + 1}}{1} = \frac{{z + 4}}{{ - 3}}\). Một vectơ chỉ phương của đường thẳng \(\Delta \) là
A. \(\overrightarrow {{u_1}} = \left( {3; - 1; - 4} \right)\).
B. \(\overrightarrow {{u_2}} = \left( { - 4; - 2;6} \right)\).
C. \(\overrightarrow {{u_3}} = \left( {2;1;3} \right)\).
D. \(\overrightarrow {{u_4}} = \left( {3;1;4} \right)\).
