Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật với \(AB = 2a\), \(AD = 5a\), \(SA = 3a\). Bằng cách thiết lập hệ trục toạ độ \(Oxyz\) như hình dưới đây, tính khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SBC} \right).\)
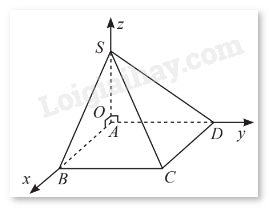
Xác định toạ độ các điểm \(A\), \(S\), \(B\), \(C\). Viết phương trình mặt phẳng \(\left( {SBC} \right)\), từ đó tính được khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SBC} \right).\)
Theo hình vẽ, toạ độ điểm \(A\) là \(A\left( {0;0;0} \right).\)
Điểm \(B\) nằm trên trục \(Ox\), \({x_B} > 0\) và \(AB = 2a\) nên toạ độ điểm \(B\) là \(B\left( {2a;0;0} \right).\)
Điểm \(S\) nằm trên trục \(Oz\), \({z_S} > 0\) và \(SA = 3a\) nên toạ độ điểm \(S\) là \(S\left( {0;0;3a} \right).\)
Điểm \(D\) nằm trên trục \(Oy\), \({y_D} > 0\) và \(AD = 5a\) nên toạ độ điểm \(D\) là \(D\left( {0;5a;0} \right).\)
Điểm \(C\) nằm trên mặt phẳng \(\left( {Oxy} \right)\), \(CB \bot Ox\), \(CD \bot Oy\) nên toạ độ điểm \(C\) là \(C\left( {2a;5a;0} \right).\)
Mặt phẳng \(\left( {SBC} \right)\) đi qua \(S\), \(B\), \(C\). Ta có \(\overrightarrow {SB} = \left( {2a;0; - 3a} \right)\) và \(\overrightarrow {BC} = \left( {0;5a;0} \right)\). Suy ra một cặp vectơ chỉ phương của mặt phẳng \(\left( {SBC} \right)\) là \(\vec u = \frac{1}{a}\overrightarrow {SB} = \left( {2;0; - 3} \right)\) và \(\vec v = \frac{1}{a}\overrightarrow {BC} = \left( {0;5;0} \right).\)
Từ đó, một vectơ pháp tuyến của mặt phẳng \(\left( {SBC} \right)\) là
\(\vec n = \left[ {\vec u,\vec v} \right] = \left( {0.0 - \left( { - 3} \right).5;\left( { - 3} \right).0 - 2.0;2.5 - 0.0} \right) = \left( {15;0;10} \right).\)
Vậy phương trình mặt phẳng \(\left( {SBC} \right)\) là
\(15\left( {x - 0} \right) + 0\left( {y - 0} \right) + 10\left( {z - 3a} \right) = 0 \Leftrightarrow 3x + 2z - 6a = 0.\)
Khoảng cách từ \(A\) đến mặt phẳng \(\left( {SBC} \right)\) là:
\(d\left( {A,\left( {SBC} \right)} \right) = \frac{{\left| {3.0 + 2.0 - 6a} \right|}}{{\sqrt {{3^2} + {2^2}} }} = \frac{{6a\sqrt {13} }}{{13}}.\)

Các bài tập cùng chuyên đề
Bài 1 :
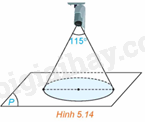
Góc quan sát ngang của một camera là \({115^0}\). Trong không gian Oxyz, camera được đặt tại điểm C(1; 2; 4) và chiếu thẳng về phía mặt phẳng \(\left( P \right):x + 2y + 2z + 3 = 0\). Hỏi vùng quan sát được trên mặt phẳng (P) của camera là hình tròn có bán kính bằng bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ nhất).
Bài 2 :
Trong không gian Oxyz, tính khoảng cách từ gốc tọa độ đến mặt phẳng \(\left( P \right):2x + 2y - z + 1 = 0\)
Bài 3 :
Cho mặt phẳng (P) có phương trình tổng quát là Ax + By + Cz + D = 0 với \(\overrightarrow n = (A;B;C)\) là vecto pháp tuyến. Cho điểm \({M_0}(2;3;4)\). Gọi \(H({x_H};{y_H};{z_H})\) là hình chiếu vuông góc của điểm \({M_0}\) trên mặt phẳng (P) (Hình 16)
a) Tính tọa độ của \(\overrightarrow {H{M_0}} \) theo \({x_H},{y_H},{z_H}\)
b) Nêu nhận xét về phương của hai vecto \(\overrightarrow n = (A;B;C)\), \(\overrightarrow {H{M_0}} \). Từ đó, hãy suy ra rằng \(\left| {\overrightarrow n .\overrightarrow {H{M_0}} } \right| = \left| {\overrightarrow n } \right|.\left| {\overrightarrow {H{M_0}} } \right| = \left| {A.2 + B.3 + C.4 + D} \right|\)
c) Tính các độ dài \(\left| {\overrightarrow n } \right|\), \(\left| {\overrightarrow {H{M_0}} } \right|\) theo A, B, C, D. Từ đó, hãy nêu công thức tính khoảng cách từ điểm \({M_0}(2;3;4)\) đến mặt phẳng (P)
Bài 4 :
Khoảng cách từ điểm M(a; b; c) đến mặt phẳng \(x - a - b - c = 0\) là:
A. \(\left| {a + b} \right|\).
B. \(\left| {b + c} \right|\).
C. \(\left| {c + a} \right|\).
D. \(\frac{{\left| {b + c} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\).
Bài 5 :
a) Tính chiều cao của hình chóp \(O.MNP\) với toạ độ các đỉnh \(O\left( {0;0;0} \right)\), \(M\left( {2;1;2} \right)\), \(N\left( {3;3;3} \right)\), \(P\left( {4;5;6} \right)\).
b) Tính khoảng cách giữa hai mặt phẳng song song \(\left( R \right):8x + 6y + 70 = 0\) và \(\left( S \right):16x + 12y - 2 = 0\)
Bài 6 :
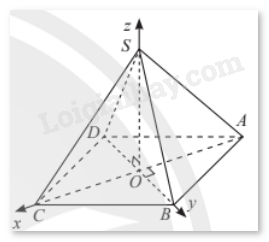
Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(a\sqrt 2 \), chiều cao bằng \(2a\) và \(O\) là tâm của đáy. Bằng cách thiết lập hệ trục toạ độ \(Oxyz\) như hình dưới đây, tính khoảng cách từ điểm \(C\) đến mặt phẳng \(\left( {SAB} \right)\).
Bài 7 :
Tính khoảng cách từ gốc toạ độ và từ điểm \(M\left( {1; - 2;13} \right)\) đến mặt phẳng \(\left( P \right):2x - 2y - z + 3 = 0.\)
Bài 8 :
Tính khoảng cách giữa hai mặt phẳng song song \(\left( P \right):x - 2 = 0\) và \(\left( Q \right):x - 8 = 0.\)
Bài 9 :
Cho mặt phẳng \(\left( P \right):3x + 4y + 2z + 4 = 0\) và điểm \(A\left( {1; - 2;3} \right)\). Khoảng cách từ \(A\) đến \(\left( P \right)\) bằng
A. \(\frac{5}{{\sqrt {29} }}\)
B. \(\frac{5}{{29}}\)
C. \(\frac{{\sqrt 5 }}{3}\)
D. \(\frac{5}{9}\)
Bài 10 :
Khoảng cách từ điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) đến mặt phẳng \(\left( {Oxy} \right)\) bằng:
A. \(\left| {{x_0}} \right|\).
B. \(\left| {{y_0}} \right|\).
C. \(\left| {{z_0}} \right|\).
D. \(\left| {{x_0} + {y_0} + {z_0}} \right|\).
Bài 11 :
Khoảng cách từ điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) đến mặt phẳng \(\left( P \right):ay + bz + c = 0\) bằng:
A. \(\frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\).
B. \(\frac{{\left| {a{x_0} + b{y_0} + c{z_0}} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\).
C. \(\frac{{\left| {a{y_0} + b{z_0} + c} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\).
D. \(\frac{{\left| {a{y_0} + b{z_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\).
Bài 12 :
Cho điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\). Tính khoảng cách từ \(M\) đến các mặt phẳng \(x - a = 0,y - b = 0,\)\(z - c = 0\).
Bài 13 :
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = 2a,AD = 3a,AA' = 4a\left( {a > 0} \right)\). Gọi \(M,N,P\) lần lượt là các điểm thuộc các tia \(AB,AD,AA'\) sao cho \(AM = a,AN = 2a,AP = 3a\). Tính khoảng cách từ điểm \(C'\) đến mặt phẳng \(\left( {MNP} \right)\).
Bài 14 :
Cho \(a + b + c \ne 0\).
Khoảng cách từ gốc toạ độ \(O\) đến mặt phẳng \(x + a + b + c = 0\) bằng:
A. \(\left| {a + b + c} \right|\).
B. \(\frac{{\left| {a + b + c} \right|}}{{{a^2} + {b^2} + {c^2}}}\).
C. \(\frac{{\sqrt {{a^2} + {b^2} + {c^2}} }}{{\left| {a + b + c} \right|}}\).
D. \(\frac{{\left| {a + b + c} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\).
Bài 15 :
Trong không gian Oxyz, khoảng cách từ điểm \(A\left( { - 2;1;0} \right)\) đến mặt phẳng \(\left( P \right):2x - 2y + z - 3 = 0\) bằng
A. 2.
B. 6.
C. 3.
D. 9.
Bài 16 :
Tính khoảng cách từ điểm \(A\left( {1;2;3} \right)\) đến các mặt phẳng sau:
a) \(\left( P \right):3x + 4z + 10 = 0\);
b) \(\left( Q \right):2x - 10 = 0\);
c) \(\left( R \right):2x + 2y + z - 3 = 0\).
Bài 17 :
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(DA = 2,DC = 3,DD = 2\).
Tính khoảng cách từ đỉnh \(B'\) đến mặt phẳng \(\left( {BA'C'} \right)\).
Bài 18 :
Cho mặt phẳng \(\left( P \right):2x + 2y + z + 10 = 0\) và điểm \(M\left( {1;1;1} \right)\). Khoảng cách từ \(M\) đến \(\left( P \right)\) bằng
A. 5.
B. \(\frac{{15}}{9}\).
C. \(\frac{{\sqrt {15} }}{3}\).
D. \(\frac{{\sqrt {15} }}{9}\).
Bài 19 :
Trong không gian Oxyz, tính khoảng cách:
a) Từ điểm \(A( - 3; - 2; - 5)\) đến mặt phẳng \((\alpha ):2x - 2y + z - 5 = 0\);
b) Giữa hai mặt phẳng \((\alpha ):y - 4 = 0\) và \((\beta ):y + 5 = 0\).
Bài 20 :
Tính khoảng cách từ điểm \(A(2;4; - 3)\) lần lượt đến các mặt phẳng sau:
a) \((\alpha ):2x - 2y + z - 9 = 0\)
b) \((\beta ):12y - 5z + 5 = 0\)
c) \((Oxy):z = 0\)
Bài 21 :
Trong không gian Oxyz, cho mặt phẳng (P): 2x – y + 2z – 4 = 0. Khoảng cách từ điểm M(3;1;-2) đến mặt phẳng (P) bằng
-
A.
\(\frac{1}{3}\)
-
B.
2
-
C.
3
-
D.
1
Bài 22 :
Trong không gian Oxyz, khoảng cách từ điểm M(1;2;-3) đến mặt phẳng (Oxy) là
-
A.
6
-
B.
3
-
C.
10
-
D.
\(\sqrt 5 \)
Bài 23 :
Trong không gian Oxyz, cho hai mặt phẳng (P): 2x – y – 2z – 9 = 0 và (Q): 4x – 2y – 4z – 6 = 0. Khoảng cách giữa hai mặt phẳng (P) và (Q) là
-
A.
0
-
B.
2
-
C.
1
-
D.
3
Bài 24 :
Trong không gian Oxyz, sàn của một căn phòng thuộc mặt phẳng (P): 3x + 4y + 5z – 6 = 0 và trần của căn phòng đó thuộc mặt phẳng (Q): 3x + 4y + 5z + 9 = 0. Hỏi chiếc tủ có chiều cao nào dưới đây không kê vừa trong căn phòng đó?
-
A.
1,8
-
B.
2
-
C.
2,2
-
D.
2,1
Bài 25 :
Khi gắn hệ trục tọa độ Oxyz (đơn vị trên mỗi trục tọa độ là decimet) vào một ngôi nhà 1 tầng, người ta thấy rằng mặt trên và mặt dưới của mái nhà thuộc các mặt phẳng vuông góc với trục Oz lần lượt thuộc mặt dưới, mặt trên của mái nhà. Biết rằng các vị trí A(2;4;25), B(5;7;27) lần lượt thuộc mặt dưới, mặt trên của của mái nhà. Độ dày của mái nhà được tính bằng khoảng cách giữa mặt trên và mặt dưới của mái nhà đó. Hãy cho biết độ dày của mái nhà đó là bao nhiêu decimet?
-
A.
0
-
B.
2
-
C.
1
-
D.
3
Bài 26 :
Trong không gian Oxyz, cho điểm \(A\left( {2; - 1; - 3} \right)\) và mặt phẳng \(\left( P \right):2x - 2y - z = 0\).
Khoảng cách từ điểm A đến mặt phẳng \(\left( P \right)\) là
A. 3.
B. 6.
C. \(\frac{2}{3}\).
D. \(\frac{1}{3}\).
Bài 27 :
Trong không gian Oxyz, khoảng cách từ điểm M(-2;1;2) đến mặt phẳng \((\alpha )\): x – 5y + 2z – 7 = 0 là
-
A.
\(\frac{{\sqrt {10} }}{3}\)
-
B.
\(\frac{{\sqrt {10} }}{{\sqrt 3 }}\)
-
C.
\(\frac{{\sqrt 3 }}{{\sqrt {10} }}\)
-
D.
\(\frac{{\sqrt 3 }}{{10}}\)
Bài 28 :
Trong không gian Oxyz, khoảng cách từ điểm M(1;4;-7) đến (P): 2x – y + 2z + 7 = 0 là
-
A.
3
-
B.
5
-
C.
7
-
D.
12
Bài 29 :
Trong không gian Oxyz, khoảng cách từ điểm A(4;1;5) đến (P): 5x – 10y + 10z – 5 = 0 bằng
-
A.
10
-
B.
\(\frac{{29}}{{100}}\)
-
C.
\(\frac{{11}}{3}\)
-
D.
\(\frac{{29\sqrt {10} }}{{10}}\)


















Danh sách bình luận