Trở lại tình huống trong Vận dụng:
Bác Châu vay ngân hàng 1,2 tỉ đồng để mua nhà theo hình thức trả góp. Số tiền bác Châu phải trả mỗi tháng bao gồm số tiền gốc phải trả hằng tháng (bằng số tiền gốc chia đều cho số tháng vay) và số tiền lãi phải trả hằng tháng (bằng số tiền gốc nhân với lãi suất tháng).
a) Nếu mỗi tháng bác Châu trả 15 triệu đồng trong 10 năm thì lãi suất năm (tính theo %) là bao nhiêu? Hãy cho biết tổng số tiền thực tế bác Châu phải trả chênh lệch bao nhiêu so với khoản vay 1,2 tỉ đồng
b) Trong công thức tĩnh lãi suất năm nói trên, hai biến x, y phải thỏa mãn các điều kiện x > 0, y > 0, xy > 1200. Em hãy giải thích ý nghĩa thực tiễn của các điều kiện này
Tính lãi suất từ 15 triệu đồng trong 10 năm từ đó đưa ra kết luận
a) Nếu trả mỗi tháng 15 triệu đồng trong 10 năm (tức là 120 tháng) thì lãi suất năm tính theo % của khoản vay là giá trị của $r=\frac{xy-1200}{100y}$ tại x = 15; y = 120 và bằng $r=\frac{15.120-1200}{100.120}=\frac{5}{100}=5%$.
Thực tế, tổng số tiền người vay trả sau 10 năm là 15.120 = 1 800 triệu đồng = 1,8 tỉ đồng, chênh (cao hơn) so với khoản vay 1,2 tỉ đồng là 0,6 tỉ đồng = 600 triệu đồng.
b) Vì x = số tiền trả mỗi tháng; y là số tháng trả góp nên x, y là số dương. Ngoài ra, xy là số tiền người vay trả sau y tháng nên nếu xy $\le $ 1 200 thì số tiền trả chưa đủ hoàn hết số tiền vay 1,2 tỉ đồng, người cho vay không có lãi hoặc lỗ. Vì vậy, trong công thức tính lãi suất năm $r=\frac{xy-1200}{100y}$, hai biến x, y phải thỏa mãn các điều kiện: x > 0; y > 0; xy > 1 200.

Các bài tập cùng chuyên đề
Bài 1 :
Một tấm bạt lớn hình chữ nhật có chiều dài \(a\) (m), chiều rộng \(b\) (m) được ghép bởi các tấm bạt bé hình chữ nhật có chiều dài và chiều rộng đều bằng \(\dfrac{1}{k}\) chiều dài, chiều rộng của tấm bạt lớn. Tính diện tích của mỗi tấm bạt bé theo \(a\), \(b\) và \(k\).
Bài 2 :
Tính:
a) \(\dfrac{{3{a^2}}}{{10{b^3}}} \cdot \dfrac{{15b}}{{9{a^4}}}\) b) \(\dfrac{{x - 3}}{{{x^2}}} \cdot \dfrac{{4x}}{{{x^2} - 9}}\)
c) \(\dfrac{{{a^2} - 6a + 9}}{{{a^2} + 3a}} \cdot \dfrac{{2a + 6}}{{a - 3}}\) d) \(\dfrac{{x + 1}}{x} \cdot \left( {x + \dfrac{{2 - {x^2}}}{{{x^2} - 1}}} \right)\)
Bài 3 :
Thực hiện các phép nhân phân thức sau:
a) \(\dfrac{{4y}}{{3{x^2}}} \cdot \dfrac{{5{x^3}}}{{2{y^3}}}\)
b) \(\dfrac{{{x^2} - 2x + 1}}{{{x^2} - 1}} \cdot \dfrac{{{x^2} + x}}{{x - 1}}\)
c) \(\dfrac{{2x + {x^2}}}{{{x^2} - x + 1}} \cdot \dfrac{{3{x^3} + 3}}{{3x + 6}}\)
Bài 4 :
Nêu quy tắc nhân hai phân số.
Bài 5 :
Thực hiện phép tính:
\(a)\dfrac{{{x^3} + 1}}{{{x^2} - 2{\rm{x}} + 1}}.\dfrac{{x - 1}}{{{x^2} - x + 1}}\)
\(b)\left( {{x^2} - 4{\rm{x}} + 4} \right).\dfrac{2}{{3{{\rm{x}}^2} - 6{\rm{x}}}}\)
Bài 6 :
Hãy nêu các tính chất của phép nhân phân số.
Bài 7 :
Thực hiện phép tính:
\(a)\dfrac{{y + 6}}{{{x^2} - 4{\rm{x}} + 4}}.\dfrac{{{x^2} - 4}}{{x + 1}}.\dfrac{{x - 2}}{{y + 6}}\)
\(b) \left(\frac{2x+1}{{x - 3}} + \frac{2x+1}{x+3}\right ) .\dfrac{{x^2 - 9}}{{2{\rm{x}} + 1}}\)
Bài 8 :
Thực hiện phép tính:
\(a)\dfrac{{3{\rm{x}} + 6}}{{4{\rm{x}} - 8}}.\dfrac{{2{\rm{x}} - 4}}{{x + 2}}\)
\(b)\dfrac{{{x^2} - 36}}{{2{\rm{x}} + 10}}.\dfrac{{x + 5}}{{6 - x}}\)
\(c)\dfrac{{1 - {y^3}}}{{y + 1}}.\dfrac{{5y + 5}}{{{y^2} + y + 1}}\)
\(d)\dfrac{{x + 2y}}{{4{{\rm{x}}^2} - 4{\rm{x}}y + {y^2}}}.\left( {2{\rm{x}} - y} \right)\)
Bài 9 :
Tính một cách hợp lí:
a) \(\dfrac{{{x^2} - 49}}{{{x^2} + 5}}.\left( {\dfrac{{{x^2} + 5}}{{x - 7}} - \dfrac{{{x^2} + 5}}{{x + 7}}} \right)\)
b) \(\dfrac{{19x + 8}}{{x + 1975}}.\dfrac{{2000 - x}}{{x + 1945}} + \dfrac{{19x + 8}}{{x + 1975}}.\dfrac{{2x - 25}}{{x + 1945}}\)
Bài 10 :
Chứng minh giá trị của mỗi biểu thức sau không phụ thuộc vào giá trị của biến:
a) \(A = \left( {\frac{1}{{x - 1}} + \frac{1}{{x + 1}}} \right)\left( {x - \frac{1}{x}} \right)\);
b) \(B = \left( {\dfrac{x}{{xy - {y^2}}} + \dfrac{{2x - y}}{{xy - {x^2}}}} \right).\dfrac{{{x^2}y - x{y^2}}}{{{{\left( {x - y} \right)}^2}}}\)
Bài 11 :
Cho phân thức \(\frac{{{x^2} - 1}}{{x + 2}}\) và \(\frac{{2 - x}}{x}\) . Hãy nhân tử với tử và mẫu với mẫu của hai phân thức này để được một phân thức mới.
Bài 12 :
Tính tích của hai phân thức \(\frac{{{x^2} - 4x + 4}}{{y - x}}\) và \(\frac{{{{\left( {x - y} \right)}^2}}}{{3{{\left( {x - 2} \right)}^3}}}\)
Bài 13 :
Tính diện tích của hình chữ nhật trong Hình 2.3 theo x.
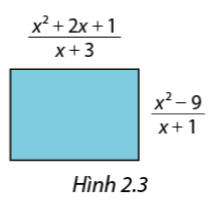
Bài 14 :
Tính nhanh: \(\frac{{{x^2} + {y^2}}}{{{x^2}}}.\frac{{{x^2} + 2xy + {y^2}}}{{{{\left( {x - y} \right)}^2}}}.\frac{{{x^2}}}{{{x^2} + {y^2}}}.\frac{{{x^2} - 2xy + {y^2}}}{{{{\left( {x + y} \right)}^2}}}\)
Bài 15 :
Rút gọn biểu thức sau theo hai cách (sử dụng và không sử dụng tính chất phân phối của phép nhân đối với phép cộng): \(\frac{{x + 1}}{x}.\left( {{x^2} - x + 1 - \frac{{{x^2}}}{{x + 1}}} \right)\).
Bài 16 :
Tính nhanh: \(\frac{t}{{{t^2} + 1}}.\frac{{x - 2y + z}}{{x + y + z}} + \frac{t}{{{t^2} + 1}}.\frac{{x + y - 2z}}{{x + y + z}} + \frac{t}{{{t^2} + 1}}.\frac{{y + z - 2x}}{{x + y + z}}\)
Bài 17 :
Thực hiện các phép nhân phân thức sau:
a) \(\frac{3}{{5a}}.\frac{{2b}}{5}\)
b) \(\frac{{2a}}{3}.\frac{6}{{4b}}\)
c) \(\frac{{{a^2}}}{{15}}.\frac{5}{a}\)
d) \(\frac{{18}}{{{a^3}}}.\frac{{{a^2}}}{{30a}}\)
Bài 18 :
Thực hiện các phép nhân phân thức sau:
a) \(\frac{{5x}}{{4y}}.\frac{{6y}}{{5{x^2}}}\);
b) \(\frac{{3{x^2}}}{{21{y^2}}}.\left( { - 7y} \right)\);
c) \(12xy.\frac{1}{{18x{y^3}}}\);
d) \(\frac{{ - 6x}}{{5y}}.\frac{{10{y^2}}}{{ - 8{x^3}}}\).
Bài 19 :
Tính:
a) \(\frac{{{x^2} - 2xy}}{y}.\frac{{{y^2}}}{x}\);
b) \(\frac{{{x^2} - 9{y^2}}}{{3x{y^2}}}.\frac{{xy}}{{x + 3y}}\);
c) \(\frac{{1 - {x^2}}}{{2x + 4y}}.\frac{{{x^2} + 4xy + 4{y^2}}}{{3 - 3x}}\);
d) \(\frac{{{x^3} - {y^3}}}{{x + y}}.\frac{{{x^2} - {y^2}}}{{{x^2} + xy + {y^2}}}\)
Bài 20 :
Thực hiện phép tính:
a) \(\frac{{24{y^5}}}{{7{x^2}}}.\left( { - \frac{{49x}}{{12{y^3}}}} \right)\)
b) \( - \frac{{36{y^3}}}{{15{x^4}}}.\left( { - \frac{{45{x^2}}}{{9{y^3}}}} \right)\)
c) \(\frac{{{x^2} - {y^2}}}{{{x^2}}}.\frac{{{x^4}}}{{{{\left( {x + y} \right)}^2}}}\)
d) \(\frac{{x + 3}}{{{x^2} - 1}}.\frac{{1 - 3x + 3{x^2} - {x^3}}}{{9x + 27}}\)
Bài 21 :
Tính một cách hợp lí:
a) \(\frac{{39x + 7}}{{x - 2020}}.\frac{{9x - 20}}{{x + 2022}} - \frac{{39x + 7}}{{x - 2020}}.\frac{{8x - 2042}}{{x + 2022}}\)
b) \(\frac{{{x^2} - 81}}{{{x^2} + 101}}.\left( {\frac{{{x^2} + 101}}{{x - 9}} + \frac{{{x^2} + 101}}{{x + 9}}} \right)\)
c) \(\frac{{{x^2} - 1}}{{x + 100}}.\frac{{2x}}{{x + 2}} + \frac{{1 - {x^2}}}{{x + 100}}.\frac{{x - 100}}{{x + 2}}\)
Bài 22 :
Vuông: \(\frac{{2{\rm{x}}}}{{x + 1}}.\frac{{x - 1}}{x} = ?\)
Pi: Nhân các tử với nhau và nhân các mẫu với nhau
Tròn: Thế cách nhân hai phân thức cũng giống như cách nhân hai phân số nhỉ?
Bài 23 :
Làm theo hướng dẫn của anh Pi trong tình huống mở đầu để nhân hai phân thức \(\frac{{2{\rm{x}}}}{{x + 1}}\) và \(\frac{{x - 1}}{x}\)
Bài 24 :
Làm tính nhân:
\(a)\frac{x}{{x + y}}.\frac{{2{\rm{x}} + 2y}}{{3{\rm{x}}y}}\)
\(b)\frac{{3{\rm{x}}}}{{4{{\rm{x}}^2} - 1}}.\frac{{ - 2{\rm{x}} + 1}}{{2{{\rm{x}}^2}}}\)
Bài 25 :
Bác Châu vay ngân hàng 1,2 tỉ đồng để mua nhà theo hình thức trả góp. Số tiền bác Châu phải trả mỗi tháng bao gồm số tiền gốc phải trả hằng tháng (bằng số tiền gốc chia đều cho số tháng vay) và số tiền lãi phải trả hằng tháng (bằng số tiền gốc nhân với lãi suất tháng).
a) Gọi r là lãi suất năm của khoản vay trả góp này. Tính số tiền x (triệu đồng) mà bác Châu phải trả mỗi thàng theo số tháng vay y (tháng) và lãi suất năm r. Từ đó suy ra công thức tính lãi suất năm r theo x và y
b) Tính giá trị của r tại x = 30, y = 48 rồi cho biết, nếu trả góp mỗi tháng 30 triệu đồng trong vòng 4 năm thì lãi suất năm (tính theo %) của khoản vay là bao nhiêu?
Bài 26 :
Làm tính nhân phân thức:
\(a)\left( { - \frac{{3{\rm{x}}}}{{5{\rm{x}}{y^2}}}} \right).\left( { - \frac{{5{y^2}}}{{12{\rm{x}}y}}} \right)\)
\(b)\frac{{{x^2} - x}}{{2{\rm{x}} + 1}}.\frac{{4{{\rm{x}}^2} - 1}}{{{x^3} - 1}}\)
Bài 27 :
Kết quả phép nhân \(\frac{{\left( {x - 3} \right)\left( {x + 3} \right)}}{{3x}}.\frac{{6x}}{{{{\left( {x - 3} \right)}^2}}}\) là
-
A.
\(\frac{2}{{x - 3}}\)
-
B.
\(\frac{{2\left( {x + 3} \right)}}{{x - 3}}\)
-
C.
\(\frac{2}{{x + 3}}\)
-
D.
\(\frac{2}{{\left( {x - 3} \right)\left( {x + 3} \right)}}\)
Bài 28 :
Thực hiện các phép tính sau:
a) \(\frac{{2{x^3}}}{{5{y^2}}}.\frac{{125{y^5}}}{{8x}}\);
b) \(\frac{{24{y^5}}}{{7{x^2}}}.\left( { - \frac{{21x}}{{12{y^3}}}} \right)\)
Bài 29 :
Tính:
a) \(\frac{{{x^2} - 6x + 9}}{{{x^2} - 3x + 9}}.\frac{{{x^3} + 27}}{{3x - 9}}\);
b) \(\frac{{2{x^2} - 20x + 50}}{{3x + 3}}.\frac{{{x^2} - 1}}{{4{{\left( {x - 5} \right)}^3}}}\)
Bài 30 :
Làm tính nhân \(\frac{x}{{x + y}}.\frac{{2x + 2y}}{{3xy}}\), ta được kết quả là
A. \(\frac{{{x^2} - 1}}{{2x - 1}}\).
B. \(\frac{{2x - 1}}{{{x^2} + 1}}\).
C. \(\frac{2}{{3y}}\).
D. \(\frac{{{x^2} - 1}}{{2x + 1}}\).



















Danh sách bình luận