Đề bài

Làm tính chia: \(\frac{{3{{x}}}}{{2{y^2}}}:\left( {\frac{{ - 5{{{x}}^2}}}{{12{y^3}}}} \right)\)

Phương pháp giải

Thực hiện theo quy tắc chia hai phân thức

Lời giải của GV Loigiaihay.com

\(\begin{array}{l}\frac{{3{{x}}}}{{2{y^2}}}:\left( {\frac{{ - 5{{{x}}^2}}}{{12{y^3}}}} \right)\\ = \frac{{3{{x}}}}{{2{y^2}}}.\frac{{12{y^3}}}{{ - 5{{{x}}^2}}}\\ = \frac{{3{{x}}.12{y^3}}}{{2{y^2}.\left( { - 5{{{x}}^2}} \right)}} = \frac{{36{{x}}{y^3}}}{{ - 10{{{x}}^2}{y^2}}} = \frac{{ - 18y}}{{5x}}\end{array}\)

Xem thêm : SGK Toán 8 - Kết nối tri thức

Báo lỗi - Góp ý

BÌNH LUẬN

Danh sách bình luận

Đang tải bình luận...

Các bài tập cùng chuyên đề

Bài 1 :

Máy A xát được \(x\) tấn gạo trong \(a\) giờ, máy B xát được \(y\) tấn gạo trong \(b\) giờ.

a) Viết các biểu thức biểu thị số tấn gạo mỗi máy xát được trong 1 giờ (gọi là công suất của máy)

b) Công suất của máy A gấp bao nhiêu lần số máy B? Viết biểu thức biểu thị số lần này.

c) Tính giá trị của biểu thức ở câu b) khi \(x = 3\), \(y = 2\), \(b = 4\)

Xem lời giải >>

Bài 2 :

Đường sắt và đường bộ từ thành phố A đến thành phố B có độ dài bằng nhau và bằng \(s\) (km). Thời gian để đi từ A đến B của tàu hỏa là \(a\) (giờ), của ô tô khách là \(b\) (giờ) (\(a < b\)). Tốc độ của tàu hỏa gấp bao nhiêu lần tốc độ của ô tô? Tính giá trị này khi \(s = 350\), \(a = 5\), \(b = 7\).

Xem lời giải >>

Bài 3 :

Thực hiện các phép chia phân thức sau:

a) \(\dfrac{{5x}}{{4{y^3}}}:\left( { - \dfrac{{{x^4}}}{{20y}}} \right)\)

b) \(\dfrac{{{x^2} - 16}}{{x + 4}} :\dfrac{{2x - 8}}{x}\)

c) \(\dfrac{{2x + 6}}{{{x^3} - 8}}:\dfrac{{{{\left( {x + 3} \right)}^3}}}{{2x - 4}}\)

Xem lời giải >>

Bài 4 :

Nêu quy tắc chia hai phân số.

Xem lời giải >>

Bài 5 :

Thực hiện phép tính

\(a)\dfrac{{x + y}}{{y - x}}:\dfrac{{{x^2} + xy}}{{3{{\rm{x}}^2} - 3{y^2}}}\)

\(b)\dfrac{{{x^3} + {y^3}}}{{x - y}}:\left( {{x^2} - xy + {y^2}} \right)\)

Xem lời giải >>

Bài 6 :

Thực hiện phép tính:

\(a)\dfrac{{20{\rm{x}}}}{{3{y^2}}}:\left( { - \dfrac{{15{{\rm{x}}^2}}}{{6y}}} \right)\)

\(b)\dfrac{{9{{\rm{x}}^2} - {y^2}}}{{x + y}}:\dfrac{{3{\rm{x}} + y}}{{2{\rm{x}} + 2y}}\)

\(c)\dfrac{{{x^3} + {y^3}}}{{y - x}}:\dfrac{{{x^2} - xy + {y^2}}}{{{x^2} - 2{\rm{x}}y + {y^2}}}\)

\(d)\dfrac{{9 - {x^2}}}{x}:\left( {x - 3} \right)\)

Xem lời giải >>

Bài 7 :

Một xí nghiệp theo kế hoạch cần phải sản xuất 120 tấn hàng trong một số ngày quy định. Do cải tiến kĩ thuật nên xí nghiệp đã hoàn thành kế hoạch sớm hơn thời gian quy định một ngày và làm thêm được 5 tấn hàng. Gọi x là số ngày xí nghiệp cần làm theo dự định. Viết phân thức biểu thị theo x:

a) Số tấn hàng xí nghiệp làm trong một ngày theo dự định.

b) Số tấn hàng xí nghiệp làm trong 1 ngày trên thực tế.

c) Tỉ số của số tấn hàng xí nghiệp làm trong 1 ngày trên thực tế và số tấn hàng xí nghiệp làm trong 1 ngày theo dự định.

Xem lời giải >>

Bài 8 :

Một ô tô chở hàng đi từ địa điểm A đến địa điểm B hết x giờ. Sau khi trả hàng tại địa điểm B, xe quay ngược trở lại địa điểm A nhưng thời gian xe chạy về đến A chỉ hết x – 1 giờ. Biết quãng đường AB dài 160 km. Viết phân thức biểu thị theo x.

a) Tốc độ xe ô tô khi chạy từ A đến B.

b) Tốc độ xe ô tô khi chạy từ B về A.

c) Tỉ số của tốc độ xe ô tô khi chạy từ A đến b và tốc độ khi chạy từ B về A.

Xem lời giải >>

Bài 9 :

Tìm biểu thức \(T\) biết: \(\frac{{{x^2} - 3x}}{{x + 2}}.T = \frac{{{x^2} - 9}}{{2{x^2} + 4x}}\).

Xem lời giải >>

Bài 10 :

Tìm biểu thức \(T\) biết: \(\frac{{{x^2} - 3x}}{{x + 2}}.T = \frac{{{x^2} - 9}}{{2{x^2} + 4x}}\).

Xem lời giải >>

Bài 11 :

Trong năm 2019, một tiệm bánh mì bán một loại bánh mì với giá \(x\) nghìn đồng một chiếc. Trong năm 2021, giá một chiếc bánh đó tăng thêm 5 nghìn đồng so với năm 2019. Một người đã dùng 900 000 đồng để mua loại bánh mì đó trong mỗi năm 2019 và 2021.

a) Viết hai phân thức lần lượt biểu diễn số bánh mì người này mua được vào năm 2019 và 2021.

b) Chứng minh rằng số bánh mì người này mua được vào năm 2019 gấp \(\frac{{x + 5}}{x}\) lần so với năm 2021.

c) Nếu \(x = 10\) thì số bánh mì người này mua được vào năm 2019 gấp bao nhiêu lần so với năm 2021.

Xem lời giải >>

Bài 12 :

Tính chiều dài của một hình chữ nhật, biết diện tích của hình chữ nhật là \(A = {x^2} - 4\) \(\left( {c{m^2}} \right)\) \(\left( {x > 3} \right)\) và chiều rộng của nó là \(\frac{{x + 2}}{{x + 1}}\left( {cm} \right)\)

Xem lời giải >>

Bài 13 :

Giả sử một xe cứu thương di chuyển về phía một người với tốc độ \(v\left( {km/h} \right)\) và bật còi báo động ở tần số \(f\) , người đó sẽ nghe được còi báo động reo ở tần số \(h\), trong đó \(h = f:\left( {1 - \frac{v}{s}} \right)\)

Và \(s\) là vận tốc của âm thanh \(\left( {s \approx 1235km/h} \right)\).

a) Chứng minh rằng \(h = \frac{{fs}}{{s - v}}\).

b) Khi xe cứu thương di chuyển về phía người đó với tốc độ 105 km/h và bật còi báo động ở tần số 45 vòng/phút, tìm tần số của còi báo động mà người này nghe được.

Xem lời giải >>

Bài 14 :

Thực hiện các phép chia phân thức sau:

a) \(\frac{{5x}}{{6y}}:\frac{{10{x^2}}}{9}\);

b) \(\frac{{ - xy}}{8}:\frac{{{x^2}}}{{4y}}\);

c) \(\frac{7}{{9{x^2}}}:\frac{{ - 14y}}{{3{x^3}}}\);

d) \(\frac{{3x}}{{2y}}:\left( {6{x^2}{y^2}} \right)\).

Xem lời giải >>

Bài 15 :

Tính:

a) \(\frac{{{x^2} - 5x}}{{4{y^2}}}:\frac{{5x}}{{2y}}\);

b) \(\frac{{{x^2} - 1}}{y}:\frac{{x + 1}}{{{y^2}}}\);

c) \(\left( {{x^2} - 2xy} \right):\frac{{5x - 10y}}{x}\);

d) \(\frac{{{x^2} - x}}{{x - y}}:\left( {{x^2} + xy} \right)\);

e) \(\left( {16 - {x^2}} \right):\left( {{x^2} - 4x} \right)\);

g) \(\frac{{4{y^2} - {x^2}}}{{{x^2} + 2xy + {y^2}}}:\frac{{x - 2y}}{{2{x^2} + 2xy}}\).

Xem lời giải >>

Bài 16 :

Năm ngoái, trên diện tích a (ha) nông trại thu hoạch được m (tấn) khoai lang. Năm nay so với năm ngoái, nông trại giảm 3 ha diện tích trồng khoai lang, nhưng nhờ cải tiến kĩ thuật, sản lượng khoai lang tăng thêm 4 tấn.

a) Năng suất khoai lang của nông trại năm nay gấp bao nhiêu lần so với năm ngoái? (Trả lời dưới dạng một phân thức.)

b) Tính giá trị của phân thức tìm được ở câu a) với \(a = 13\) và \(m = 156\).

Xem lời giải >>

Bài 17 :

Kết quả của phép chia \(\frac{{{x^2} - {y^2}}}{{6xy}}:\frac{{x - y}}{{3y}}\) là

A. \(\frac{{x + y}}{{2x}}\)

B. \(\frac{{x + y}}{{18x}}\)

C. \(\frac{{2\left( {x + y} \right)}}{x}\)

D. \(\frac{{x + y}}{{18x{y^2}}}\)

Xem lời giải >>

Bài 18 :

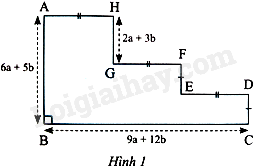
Ở hình bên, độ dài các cạnh AB, BC và GH được cho theo a và b; hai cạnh CD và EF bằng nhau; ba cạnh AH, GF và ED bằng nhau.

a) Tìm độ dài các cạnh AH, GF, ED.

b) Tìm độ dài các cạnh CD, EF.

c) Tính chu vi của hình bên.

Xem lời giải >>

Bài 19 :

Thực hiện phép tính:

a) \(\frac{1}{{{x^2} - x + 1}}:\frac{{x + 1}}{{x - 1}}\)

b) \(\frac{{x + y}}{{2x - y}}:\frac{1}{{x - y}}\)

c) \(\frac{{{x^3}y + x{y^3}}}{{{x^4}y}}:\left( {{x^2} + {y^2}} \right)\)

d) \(\frac{{{x^3} + 8}}{{{x^2} - 2x + 1}}:\frac{{{x^2} + 3x + 2}}{{1 - {x^2}}}\)

Xem lời giải >>

Bài 20 :

Hai máy bay cùng bay quãng đường 600 km. Biết tốc độ của máy bay thứ hai lớn hơn tốc độ của máy bay thứ nhất là 300 km/h. Gọi \(x\) (km/h) là tốc độ của máy bay thứ nhất \(\left( {x > 0} \right)\). Viết phân thức biểu thị theo \(x\).

a) Thời gian máy bay thứ nhất đã bay

b) Thời gian máy bay thứ hai đã bay

c) Tỉ số của thời gian máy bay thứ nhất đã bay và thời gian máy bay thứ hai đã bay.

Xem lời giải >>

Bài 21 :

Thương của phép chia phân thức \(\frac{{{y^3} - {x^3}}}{{6{x^3}y}}\) cho phân thức \(\frac{{{x^2} + xy + {y^2}}}{{2xy}}\) là:
A. \(\frac{{y - x}}{{3x}}\)
B. \(\frac{{x - y}}{{3{x^2}}}\)
C. \(\frac{{x - y}}{{3x}}\)
D. \(\frac{{y - x}}{{3{x^2}}}\)

Xem lời giải >>

Bài 22 :

Một tổ sản xuất theo kế hoạch phải may 600 chiếc khẩu trang trong thời gian quy định. Do tăng năng suất lao động, mỗi giờ tổ sản xuất đó may được nhiều hơn kế hoạch 20 chiếc. Gọi \(x\) là số khẩu trang mà tổ sản xuất phải may trong mỗi giờ theo kế hoạch \(\left( {x \in \mathbb{N}*,x < 600} \right)\). Viết phân thức biểu thị theo \(x\).

a) Thời gian tổ sản xuất phải hoàn thành công việc theo kế hoạch.

b) Thời gian tổ sản xuất đã hoàn thành công việc theo thực tế.

c) Tỉ số của thời gian tổ sản xuất đã hoàn thành công việc theo thức tế và thời gian tổ sản xuất phải hoàn thành công việc theo kế hoạch.

Xem lời giải >>

Bài 23 :

Kết luận sau là đúng hay sai?

\(\left( {\frac{1}{x}:\frac{1}{x}} \right):\frac{1}{x} = \frac{1}{x}:\left( {\frac{1}{x}:\frac{1}{x}} \right)\)

Xem lời giải >>

Bài 24 :

Thực hiện phép tính:

\(a)\left( { - \frac{{3{\rm{x}}}}{{5{\rm{x}}{y^2}}}} \right):\left( { - \frac{{5{y^2}}}{{12{\rm{x}}y}}} \right)\)

\(b)\frac{{4{{\rm{x}}^2} - 1}}{{8{{\rm{x}}^3} - 1}}:\frac{{4{{\rm{x}}^2} + 4{\rm{x}} + 1}}{{4{{\rm{x}}^2} + 2{\rm{x}} + 1}}\)

Xem lời giải >>

Bài 25 :

Tìm \(x\) biết \(\frac{{a + 1}}{{a + 2}}.x = \frac{{{a^2} - 1}}{{{a^2} + 2a}}\), với \(a\) là hằng số; \(a \ne 1;\,\,a \ne - 1;\,\,a \ne 0;\,\,a \ne - 2\)

A.

$\frac{a}{a - 1}$
B.

$\frac{a - 1}{a}$
C.

$\frac{a}{2 (a - 1)}$
D.

$\frac{a - 1}{2 a}$

Xem lời giải >>

Bài 26 :

Phép tính \(\frac{{3{{\left( {x - y} \right)}^2}}}{5}:\frac{{10x - 10y}}{{x + y}}\) có kết quả là:

A.

\(\frac{{3{x^2} - {y^2}}}{{50}}\)
B.

\(\frac{{3\left( {{x^2} + {y^2}} \right)}}{{50}}\)
C.

\(\frac{{3\left( {{x^2} - {y^2}} \right)}}{{50}}\)
D.

\(\frac{{3{x^2} + {y^2}}}{{50}}\)

Xem lời giải >>

Bài 27 :

Tính:

a) \(\frac{{{x^2} - {y^2}}}{{6{x^2}y}}:\frac{{x + y}}{{3xy}}\);

b) \(16{x^2}{y^2}:\left( { - \frac{{18{x^2}{y^5}}}{5}} \right);\)

c) \(\frac{{1 - 4{x^2}}}{{{x^2} + 4x}}:\frac{{2 - 4x}}{{3x}}\).

Xem lời giải >>

Bài 28 :

Hai công nhân cùng làm một mặt hàng. Người công nhân thứ nhất làm được 1 000 sản phẩm trong x (giờ); người công nhân thứ hai làm được 1 250 sản phẩm trong \(x + 10\) (giờ)

a) Viết các phân thức biểu thị số sản phẩm người thứ nhất làm được trong 1 giờ; số sản phẩm người công nhân thứ hai làm được trong 1 giờ; tỉ số giữa năng suất của người công nhân thứ hai so với năng suất của người công nhân thứ nhất.

b) Tính giá trị tỉ số giữa năng suất của người công nhân thứ hai so với năng suất của người công nhân thứ nhất trong trường hợp \(x = 240\). Hãy cho biết trong trường hợp này, năng suất lao động của người công nhân thứ hai tăng bao nhiêu phần trăm so với năng suất lao động của người công nhân thứ nhất.

Xem lời giải >>

Bài 29 :

Làm tính chia \(\frac{1}{x}:\frac{1}{x}:\frac{1}{x}\), ta được kết quả là

A. \(\frac{1}{{{x^3}}}\).

B. \(1\).

C. \(\frac{1}{x}\).

D. \(x\).

Xem lời giải >>

Bài 30 :

Làm tính chia phân thức:

a) \(\left( { - \frac{{3{\rm{x}}}}{{5{\rm{x}}{y^2}}}} \right):\left( { - \frac{{5{y^2}}}{{12{\rm{x}}y}}} \right)\);

b) \(\frac{{4{{\rm{x}}^2} - 1}}{{8{{\rm{x}}^3} - 1}}:\frac{{4{{\rm{x}}^2} + 4{\rm{x}} + 1}}{{4{{\rm{x}}^2} + 2{\rm{x}} + 1}}\).

Xem lời giải >>