Quan sát hình căn phòng, hãy cho biết vị trí tương đối của các cặp đường thẳng \(a\) và \(b\), \(a\) và \(c\), \(b\) và \(c\).
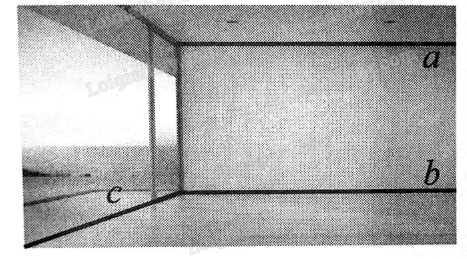
Quan sát hình và chỉ ra vị trí tương đối của từng cặp đường thẳng có trong hình
Nhìn hình vẽ, ta thấy \(a\) và \(c\) không cùng thuộc một mặt phẳng nào, nên 2 đường thẳng này chéo nhau.
Ta có \(b\) và \(c\) cùng thuộc mặt phẳng “sàn nhà”. Nhìn theo hình, ta thấy chúng cắt nhau tại một điểm ở góc phòng. Như vậy \(b\) và \(c\) cắt nhau.
Ta có \(a\) và \(b\) cùng thuộc mặt phẳng “tường nhà”. Nhìn theo hình, ta thấy hai đường thẳng không có điểm chung. Do đó \(a\) và \(b\) song song với nhau.

Các bài tập cùng chuyên đề
Bài 1 :
Cho hai đường thẳng phân biệt a và b trong không gian. Có bao nhiêu vị trí tương đối giữa a và b?
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Bài 2 :
Trong không gian, cho 3 đường thẳng a, b, c, biết a // b, a và c chéo nhau. Khi đó hai đường thẳng b và c
-
A.
Trùng nhau hoặc chéo nhau.
-
B.
Cắt nhau hoặc chéo nhau.
-
C.
Chéo nhau hoặc song song.
-
D.
Song song hoặc trùng nhau.
Bài 3 :
Một chiếc gậy được đặt một đầu dựa vào tường và đầu kia trên mặt sàn (H.4.20). Hỏi có thể đặt chiếc gậy đó song song với một trong các mép tường hay không?

Bài 4 :
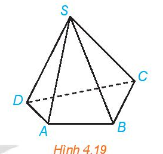
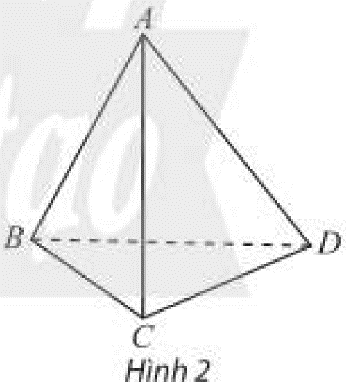
Trong hình chóp tứ giác S.ACBD (H.4.19), chỉ ra những đường thẳng:
a) Chéo với đường thẳng SA
b) Chéo vói đường thẳng BC
Bài 5 :
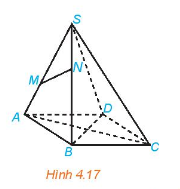
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành (H.4.17)
a) Trong các đường thẳng AB, AC, CD, hai đường thẳng nào song song, hai đường thẳng nào cắt nhau?
b) Gọi M, N lần lượt là hai điểm thuộc hai cạnh SA, SB. Trong các đường thẳng SA, MN, AB có hai đường thẳng nào chéo nhau hay không?
Bài 6 :
Hãy tìm một số hình ảnh về hai đường thẳng song song, hai đường thẳng chéo nhau trong thực tiễn
Bài 7 :

Hình 4.13 minh hoạt bốn tuyến đường (được coi là thẳng) tại một nút giao ở Hà Nội.
Quan sát tình ảnh đó và trả lời các câu hỏi sau:
a) Hai tuyến đường nào giao nhau?
b) Hai tuyến đường nào không giao nhau?
c) Hai tuyến đường nào song song?
Bài 8 :
Cho hình chóp S.ABCD có đáy là hình bình hành. Trong các cặp đường thẳng sau, cặp đường thẳng nào cắt nhau, cặp đường thẳng nào song song, cặp đường thẳng nào chéo nhau?
a) AB và CD
b) AC và BD
c) SB và CD
Bài 9 :
Cho đường thẳng a song song với mặt phẳng (P). Mặt phẳng (Q) chứa đường thẳng a và cắt mặt phẳng (P) theo giao tuyến là đường thẳng b. Vị trí tương đối của hai đường thẳng a và b là:
A. chéo nhau
B. cắt nhau
C. song song
D. trùng nhau
Bài 10 :
Quan sát một phần căn phòng (Hình 35), hãy cho biết vị trí tương đối của các cặp đường thẳng a và b; a và c; b và c.

Bài 11 :
a) Hãy nêu các vị trí tương đối của hai đường thẳng trong mặt phẳng.
b) Quan sát hai đường thẳng a và b trong Hình 31a, 31b và cho biết các đường thẳng đó có cùng nằm trong một mặt phẳng không

Bài 12 :
Quan sát phòng học của lớp và nêu lên hình ảnh của hai đường thẳng song song, cắt nhau, chéo nhau.
Bài 13 :
Quan sát Hình 43 và cho biết vị trí tương đối của hai trong ba cột tuabin gió có trong hình.

Bài 14 :
Cho hai đường thẳng phân biệt a và b trong không gian. Có bao nhiêu vị trí tương đối giữa a và b?
A. 1
B. 2
C. 3
D. 4
Bài 15 :
Hãy chỉ ra các ví dụ về hai đường thẳng song song, cắt nhau và chéo nhau trong hình cầu sắt ở Hình 6.

Bài 16 :
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Xét vị trí tương đối của các cặp đường thẳng sau đây:
a) \(AB\) và \(CD\);
b) \(SA\) và \(SC\);
c) \(SA\) và \(BC\).
Bài 17 :
a) Nếu các trường hợp có thể xảy ra đối với hai đường thẳng \(a,b\) cùng nằm trong một mặt phẳng.
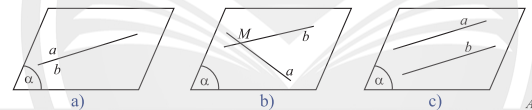
b) Cho tứ diện \(ABCD\). Hai đường thẳng \(AB\) và \(CD\) có cùng nằm trong bất kì mặt phẳng nào không?
Bài 18 :
Chỉ ra các đường thẳng song song trong mỗi hình sau. Tìm thêm một số ví dụ khác về các đường thẳng song song trong thực tế.

Bài 19 :
Trong không gian, cho ba đường thẳng \(a,b,c\) biết \(a\,{\rm{//}}\,b\) và \(a\), \(c\) chéo nhau. Khi đó hai đường thẳng \(b\) và \(c\) sẽ
-
A.
Trùng nhau hoặc chéo nhau
-
B.
Cắt nhau hoặc chéo nhau
-
C.
Chéo nhau hoặc song song
-
D.
Song song hoặc trùng nhau
Bài 20 :
Cho tứ diện \(ABCD\). Gọi \(I,J\) lần lượt là trọng tâm các tam giác \(ABC\) và \(ABD\). Khẳng định nào sau đây là đúng?
-
A.
\(IJ\) song song với \(CD\)
-
B.
\(IJ\) song song với \(AB\)
-
C.
\(IJ\) chéo \(CD\)
-
D.
\(IJ\) cắt \(AB\)
Bài 21 :
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Hỏi cạnh \(CD\) chéo với tất cả các cạnh nào của hình chóp?
-
A.
\(SA;\,AB\)
-
B.
\(SA;\,SB\)
-
C.
\(SB;AB\)
-
D.
\(SB;\,AD\)
Bài 22 :
Trong không gian, cho ba đường thẳng \(a,\,\,b,\,\,c\). Trong các mệnh đề sau mệnh đề nào đúng?
-
A.
Nếu \(a\) và \(b\) không cắt nhau thì \(a\) và \(b\) song song
-
B.
Nếu \(b\) và \(c\) chéo nhau thì \(b\) và \(c\) không cùng thuộc một mặt phẳng
-
C.
Nếu \(a\) và \(b\) cùng chéo nhau với \(c\) thì \(a\) song song với \(b\)
-
D.
Nếu \(a\) và \(b\) cắt nhau, \(b\) và \(c\) cắt nhau thì \(a\) và \(c\) cắt nhau
Bài 23 :
Trong các mệnh đề sau, mệnh đề nào đúng?
-
A.
Hai đường thẳng có một điểm chung thì chúng có vô số điểm chung khác.
-
B.
Hai đường thẳng song song khi và chỉ khi chúng không có điểm chung.
-
C.
Hai đường thẳng song song khi và chỉ khi chúng không đồng phẳng.
-
D.
Hai đường thẳng chéo nhau khi và chỉ khi chúng không đồng phẳng.
Bài 24 :
Hai đường thẳng chéo nhau khi và chỉ khi:
A. Hai đường thẳng cùng nằm trong một mặt phẳng và không có điểm chung.
B. Hai đường thẳng không có điểm chung
C. Hai đường thẳng không cùng nằm trong một mặt phẳng nào.
D. Hai đường thẳng cùng chéo nhau với đường thẳng thứ ba.
Bài 25 :
Cho ba đường thẳng \(a\), \(b\), \(c\). Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu \(a\) và \(b\) cùng song song với \(c\) thì \(a\) song song với \(b\).
B. Nếu \(a\) và \(b\) cùng chéo nhau với \(c\) thì \(a\) và \(b\) chéo nhau.
C. Nếu \(a\) song song với \(b\), \(b\) và \(c\) chéo nhau thì \(a\) và \(c\) chéo nhau hoặc cắt nhau.
D. Nếu \(a\) và \(b\) cắt nhau, \(b\) và \(c\) cắt nhau thì \(a\) và \(c\) cắt nhau.
Bài 26 :
Trong không gian cho hai đường thẳng cắt nhau a và b. Nếu c là một đường thẳng song song với a thì
A. c và b song song
B. c và b cắt nhau
C. c và b chéo nhau
D. c và b không song song với nhau
Bài 27 :
Trong không gian, hai đường thẳng không có điểm chung thì
A. cắt nhau.
B. chéo nhau hoặc song song.
C. chéo nhau.
D. song song.
Bài 28 :
Trong các mệnh đề sau, mệnh đề nào đúng?
-
A.
Hai đường thẳng không có điểm chung là hai đường thẳng song song hoặc chéo nhau.
-
B.
Hai đường thẳng chéo nhau thì chúng có điểm chung.
-
C.
Hai đường thẳng song song khi chúng ở trên cùng một mặt phẳng.
-
D.
Khi hai đường thẳng ở trên hai mặt phẳng thì hai đường thẳng đó chéo nhau.
Bài 29 :
Cho hình hộp $ABCD.EFGH$. Mệnh đề nào sau đây sai?
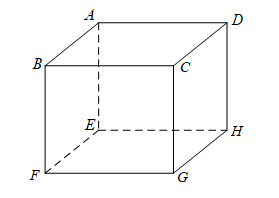
-
A.
$BG$ và $HD$ chéo nhau.
-
B.
$BF$ và $AD$ chéo nhau.
-
C.
$AB$ song song với $HG$.
-
D.
$CG$ cắt $HE$.
Bài 30 :
Cho hình hộp \(ABCD.A'B'C'D'\) có 6 mặt đều là hình vuông.
a) Tìm các đường thẳng đi qua hai đỉnh của hình lập phương và vuông góc với \(AC\).
b) Trong các đường thẳng tìm được ở câu a, tìm đường thẳng chéo với \(AC\).


















Danh sách bình luận