Cho hai dãy số \(\left( {{u_n}} \right)\), \(\left( {{v_n}} \right)\) với \({u_n} = 3 - \frac{4}{{n + 1}}\), \({v_n} = 8 - \frac{5}{{3{n^2} + 2}}\). Tính:
a) \(\lim {u_n}\), \(\lim {v_n}\)
b) \(\lim \left( {{u_n} + {v_n}} \right)\), \(\lim \left( {{u_n} - {v_n}} \right)\), \(\lim \left( {{u_n}.{v_n}} \right)\), \(\lim \frac{{{u_n}}}{{{v_n}}}\)
Sử dụng tính chất về dãy số có giới hạn vô cực.
Sử dụng định lí về giới hạn hữu hạn: Nếu \(\lim {u_n} = a\), \(\lim {v_n} = b\) thì:
\(\lim \left( {{u_n} + {v_n}} \right) = a + b\), \(\lim \left( {{u_n} - {v_n}} \right) = a - b\), \(\lim \left( {{u_n}.{v_n}} \right) = ab\)
Trường hợp \({v_n} \ne 0\) và \(b \ne 0\), ta có \(\lim \frac{{{u_n}}}{{{v_n}}} = \frac{a}{b}\)
a)
Ta có \(\lim 4 = 4\) và \(\lim \left( {n + 1} \right) = + \infty \), nên \(\lim \frac{4}{{n + 1}} = 0\).
Sử dụng định lí về giới hạn hữu hạn, ta có:
\(\lim {u_n} = \lim \left( {3 - \frac{4}{{n + 1}}} \right) = \lim 3 - \lim \frac{4}{{n + 1}} = 3 - 0 = 3\)
Chứng minh tương tự, ta cũng có:
\(\lim {v_n} = \lim \left( {8 - \frac{5}{{3{n^2} + 2}}} \right) = \lim 8 - \lim \frac{5}{{3{n^2} + 2}} = 8 - 0 = 8\)
b) Theo kết quả câu a, ta có \(\lim {u_n} = 3\), \(\lim {v_n} = 8 \ne 0\).
Sử dụng định lí về giới hạn hữu hạn, ta có:
\(\lim \left( {{u_n} + {v_n}} \right) = \lim {u_n} + \lim {v_n} = 3 + 8 = 11\)
\(\lim \left( {{u_n} - {v_n}} \right) = \lim {u_n} - \lim {v_n} = 3 - 8 = - 5\)
\(\lim \left( {{u_n}.{v_n}} \right) = \lim {u_n}.\lim {v_n} = 3.8 = 24\)
\(\lim \frac{{{u_n}}}{{{v_n}}} = \frac{{\lim {u_n}}}{{\lim {v_n}}} = \frac{3}{8}\) (do \({v_n} \ne 0\) với \(\forall n \in {\mathbb{N}^*}\))
Các bài tập cùng chuyên đề
Một bệnh nhân hàng ngày phải uống một viên thuốc 150 mg. Sau ngày đầu, trước mỗi lần uống, hàm lượng thuốc cũ trong cơ thể vẫn còn 5%. Tính lượng thuốc có trong cơ thể sau khi uống viên thuốc của ngày thứ 5. Ước tính lượng thuốc trong cơ thể nếu bệnh nhân sử dụng thuốc trong một thời gian dài.
Cho tam giác vuông ABC vuông tại A, có AB = h và góc B bằng \(\alpha \) (H.5.3). Từ A kẻ \(A{A_1} \bot BC\), từ \({A_1}\) kẻ \({A_1}{A_2} \bot AC\), sau đó lại kẻ \({A_2}{A_3} \bot BC\). Tiếp tục quá trình trên, ta được đường gấp khúc vô hạn \(A{A_1}{A_2}{A_3} \ldots \) Tính độ dài đường gấp khúc này theo h và \(\alpha \)
Viết các số thập phân vô hạn tuần hoàn sau đây dưới dạng phân số.
a) \(1,\left( {01} \right)\); b) \(5,\left( {132} \right)\)
Tính các giới hạn sau:
a) \(\lim \frac{{5n + 1}}{{2n}};\)
b) \(\lim \frac{{6{n^2} + 8n + 1}}{{5{n^2} + 3}};\)
c) \(\lim \frac{{\sqrt {{n^2} + 5n + 3} }}{{6n + 2}};\)
d) \(\lim \left( {2 - \frac{1}{{{3^n}}}} \right);\)
e) \(\lim \frac{{{3^n} + {2^n}}}{{{{4.3}^n}}};\)
g) \(\lim \frac{{2 + \frac{1}{n}}}{{{3^n}}}.\)
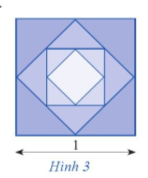
Từ hình vuông có độ dài cạnh bằng 1, người ta nối các trung điểm của cạnh hình vuông để tạo ra hình vuông mới như Hình 3. Tiếp tục quá trình này đến vô hạn.
a) Tính diện tích \({S_n}\) của hình vuông được tạo thành ở bước thứ n;
b) Tính tổng diện tích của tất cả các hình vuông được tạo thành.
Có 1 kg chất phóng xạ độc hại. Biết rằng, cứ sau một khoảng thời gian T= 24 000 năm thì một nửa số chất phóng xạ này bị phân rã thành chất khác không độc hại đối với sức khỏe của con người (T được gọi là chu kì bán rã).
(Nguồn: Đại số và Giải tích 11, NXBGD Việt Nam, 2021)
Gọi \({u_n}\) là khối lượng chất phóng xạ còn lại sau chu kì thứ n.
a) Tìm số hạng tổng quát \({u_n}\) của dãy số \(\left( {{u_n}} \right)\).
b) Chứng minh rằng \(\left( {{u_n}} \right)\) có giới hạn là 0.
c) Từ kết quả câu b), chứng tỏ rằng sau một số năm nào đó khối lượng chất phóng xạ đã cho ban đầu không còn độc hại đối với con người, biết rằng chất phóng xạ này sẽ không độc hại nữa nếu khối lượng chất phóng xạ còn lại bé hơn \({10^{ - 6}}\) g.
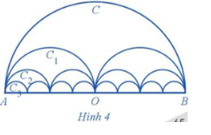
Gọi C là nửa đường tròn đường kính AB = 2R, C1 là đường gồm hai nửa đường tròn đường kính \(\frac{{AB}}{2},\), C2 là đường gồm bốn nửa đường tròn đường kính \(\frac{{AB}}{4},...\)
Gọi pn là độ dài của Cn, Sn là diện tích hình phẳng giới hạn bởi Cn và đoạn thẳng AB.
a) Tính pn, Sn.
b) Tìm giới hạn của các dãy số (pn) và (Sn).
Tính các giới hạn sau:
a) \(\lim \frac{{2{n^2} + 6n + 1}}{{8{n^2} + 5}}\)
b) \(\lim \frac{{4{n^2} - 3n + 1}}{{ - 3{n^3} + 5{n^2} - 2}}\);
c) \(\lim \frac{{\sqrt {4{n^2} - n + 3} }}{{8n - 5}}\);
d) \(\lim \left( {4 - \frac{{{2^{n + 1}}}}{{{3^n}}}} \right)\)
e) \(\lim \frac{{{{4.5}^n} + {2^{n + 2}}}}{{{{6.5}^n}}}\)
g) \(\lim \frac{{2 + \frac{4}{{{n^3}}}}}{{{6^n}}}\).
Từ độ cao \(55,8\;{\rm{m}}\) của tháp nghiêng Pisa nước Ý, người ta thả một quả bóng cao su chạm xuống đất (Hình 18). Giả sử mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng \(\frac{1}{{10}}\) độ cao mà quả bóng đạt được trước đó. Gọi \({S_n}\) là tổng độ dài quãng đường di chuyển của quả bóng tính từ lúc thả ban đầu cho đến khi quả bóng đó chạm đất \(n\) lần. Tính \(\lim {S_n}\).
Cho một tam giác đều ABC cạnh \(a\). Tam giác \({A_1}{B_1}{C_1}\) có các đỉnh là trung điểm các cạnh của tam giác ABC, tam giác \({A_2}{B_2}{C_2}\) có các đỉnh là trung điểm các cạnh của tam giác \({A_1}{B_1}{C_1}, \ldots \), tam giác \({A_{n + 1}}{B_{n + 1}}{C_{n + 1}}\) có các đỉnh là trung điểm các cạnh của tam giác \({A_n}{B_n}{C_n}, \ldots \) Gọi \({p_1},{p_2}, \ldots ,{p_n}, \ldots \) và \({S_1},{S_2}, \ldots ,{S_n}, \ldots \) theo thứ tự là chu vi và diện tích của các tam giác \({A_1}{B_1}{C_1},{A_2}{B_2}{C_2}, \ldots ,{A_n}{B_n}{C_n}, \ldots \).
a) Tìm giới hạn của các dãy số \(\left( {{p_n}} \right)\) và \(\left( {{S_n}} \right)\).
b) Tìm các tổng \({p_1} + {p_2} + \ldots + {p_n} + \ldots \) và \({S_1} + {S_2} + \ldots + {S_n} + \ldots \).
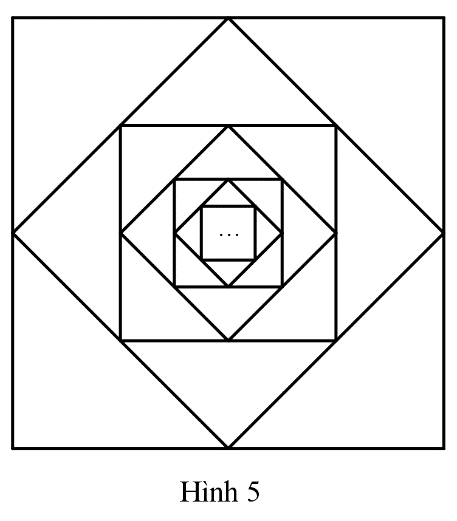
Từ hình vuông đầu tiên có cạnh bằng 1 (đơn vị độ dài), nối các trung điểm của bốn cạnh để có hình vuông thứ hai. Tiếp tục nối các trung điểm của bốn cạnh của hình vuông thứ hai để được hình vuông thứ ba. Cứ tiếp tục làm như thế, nhận được một dãy hình vuông (xem Hình 5).
a) Kí hiệu \({a_n}\) là diện tích của hình vuông thứ \(n\) và \({S_n}\) là tổng diện tích của \(n\) hình vuông đầu tiên. Viết công thức tính \({a_n},{S_n}\left( {n = 1,2,3,...} \right)\) và tìm \(\lim {S_n}\) (giới hạn này nếu có được gọi là tổng diện tích của các hình vuông).
b) Kí hiệu \({p_n}\) là chu vi của hình vuông thứ \(n\) và \({Q_n}\) là tổng chu vi của \(n\) hình vuông đầu tiên. Viết công thức tính \({p_n}\) và \({Q_n}\left( {n = 1,2,3,...} \right)\) và tìm \(\lim {Q_n}\) (giới hạn này nếu có được gọi là tổng chu vi của các hình vuông).
Xét quá trình tạo ra hình có chu vi vô cực và diện tích bằng 0 như sau:
Bắt đầu bằng một hình vuông \({H_0}\) cạnh bằng 1 đơn vị độ dài (xem Hình 6a). Chia hình vuông \({H_0}\) thành chính hình vuông bằng nhau, bỏ đi bốn hình vuông, nhận được hình \({H_1}\) (xem Hình 6b). Tiếp theo, chia mỗi hình vuông của \({H_1}\) thành chín hình vuông, rồi bỏ đi bốn hình vuông, nhận được hình \({H_2}\) (xem Hình 6c). Tiếp tục quá trình này, ta nhận được một dãy hình \({H_n}\left( {n = 1,2,3,...} \right)\).
Ta có: \({H_1}\) có 5 hình vuông, mỗi hình vuông có cạnh bằng \(\frac{1}{3}\);
\({H_2}\) có \(5.5 = {5^2}\) hình vuông, mỗi hình vuông có cạnh bằng \(\frac{1}{3}.\frac{1}{3} = \frac{1}{{{3^2}}}\);…
Từ đó, nhận được hình \({H_n}\) có \({5^n}\) hình vuông, mỗi hình vuông có cạnh bằng \(\frac{1}{{{3^n}}}\).
a) Tính diện tích \({S_n}\) của \({H_n}\) và tính \(\lim {S_n}\).
b) Tính chu vi \({p_n}\) của \({H_n}\) và tính \(\lim {p_n}\).
(Quá trình trên tạo nên một hình, gọi là một fractal, được coi là có diện tích \(\lim {S_n}\) và chu vi \(\lim {p_n}\)).
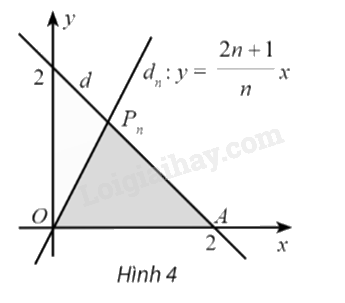
Trong mặt phẳng tọa độ Oxy, đường thẳng \(d:x + y = 2\) cắt trục hoành tại điểm A và cắt đường thẳng \({d_n}:y = \frac{{2n + 1}}{n}x\) tại điểm \({P_n}\left( {n \in \mathbb{N}*} \right)\). Kí hiệu \({S_n}\) là diện tích của tam giác \(OA{P_n}\). Tính \(\lim {S_n}\).
Cho \(a > b > 0\) và \(\lim \frac{{{a^{n + 1}} + {b^n}}}{{2{a^n} + {b^{n + 1}}}} = 1\). Tìm giá trị của a.
Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn \(\lim n{u_n} = \frac{1}{2}\). Tìm \(\lim \left( {3n - 4} \right){u_n}\).
Phát biểu nào sau đây là SAI?
A. \(\lim \frac{1}{{{2^n}}} = 0\)
B. \(\lim {\left( {\frac{3}{2}} \right)^n} = 0\)
C. \(\lim \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}} = 0\)
D. \(\lim {\left( { - \frac{{\sqrt 3 }}{2}} \right)^n} = 0\)
Chứng minh rằng \(\lim \frac{{{{\left( { - 1} \right)}^n}}}{{{n^2}}} = 0\).
Tính các giới hạn sau:
a) \(\lim \frac{{4n + 2}}{3}\)
b) \(\lim \frac{{3n + 4}}{{ - 5 + \frac{2}{n}}}\)
c) \(\lim \frac{{ - 3 + \frac{1}{{n + 1}}}}{{{5^n}}}\)
d) \(\lim \left( {6 - \frac{5}{{{4^n}}}} \right)\)
Tính các giới hạn sau:
a) \(\lim \frac{{6n - 5}}{{3n}}\)
b) \(\lim \frac{{ - 2{n^2} - 6n + 2}}{{8{n^2} - 5n + 4}}\)
c) \(\lim \frac{{{n^3} - 5n + 1}}{{3{n^2} - 4n + 2}}\)
d) \(\lim \frac{{ - 4n + 1}}{{9{n^2} - n + 2}}\)
e) \(\lim \frac{{\sqrt {4{n^2} + n + 1} }}{{8n + 3}}\)
g) \(\lim \frac{{{4^n} + {5^n}}}{{{{3.4}^n} - {{4.5}^n}}}\)
Từ độ cao 100 m, người ta thả một quả bóng cao su xuống đất. Giả sử cứ sau mỗi lần chạm đất, quả bóng nảy lên một độ cao bằng \(\frac{1}{4}\) độ cao mà quả bóng đạt được trước đó. Gọi \({h_n}\) là độ cao quả bóng đạt được ở lần nảy thứ \(n\).
a) Tìm số hạng tổng quát của dãy số \(\left( {{h_n}} \right)\).
b) Tính giới hạn của dãy số \(\left( {{h_n}} \right)\) và nêu ý nghĩa giới hạn của dãy số \(\left( {{h_n}} \right)\).
c) Gọi \({S_n}\) là tổng độ dài quãng đường đi được của quả bóng từ lúc bắt đầu thả quả bóng đến khi quả bóng chạm đất lần thứ \(n\). Tính \({S_n}\), nếu quá trình này cứ tiếp tục diễn ra mãi thì tổng quãng đường quả bóng di chuyển được là bao nhiêu?
Tính các giới hạn sau:
a) \(\lim \frac{{2n - 4}}{5}\)
b) \(\lim \frac{{1 + \frac{1}{{2n}}}}{{2n}}\)
c) \(\lim \left( {2 + \frac{7}{{{4^n}}}} \right)\)
d) \(\lim \frac{{ - 4{n^2} - 3}}{{2{n^2} - n + 5}}\)
e) \(\lim \frac{{\sqrt {9{n^2} + 2n + 1} }}{{n - 5}}\)
g) \(\lim \frac{{{3^n} + {{4.9}^n}}}{{{{3.4}^n} + {9^n}}}\)
Cho \({u_n} = \frac{{1 + a + {a^2} + ... + {a^n}}}{{1 + b + {b^2} + ... + {b^n}}}\) với a, b là các số thực thỏa mãn \(\left| a \right| < 1,\left| b \right| < 1\). Tìm \(\mathop {\lim }\limits_{n \to + \infty } {u_n}\)
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_1} = 2,{u_{n + 1}} = {u_n} + \frac{2}{{{3^n}}},n \ge 1\). Đặt \({v_n} = {u_{n + 1}} - {u_n}.\)
a) Tính \({v_1} + {v_2} + ... + {v_n}\) theo n.
b) Tính \({u_n}\) theo n.
c) Tìm \(\mathop {\lim }\limits_{n \to + \infty } {u_n}\)
Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn \(\left| {{u_n} - 2} \right| < \frac{1}{{{n^3}}}\) với mọi \(n \in {\mathbb{N}^*}\). Khi đó
Giả sử \({u_n}\) là số hạng thứ \(n\) của dãy số \(\left( {{u_n}} \right)\) và \({u_n} = \frac{{{{\left( {1 + \sqrt 5 } \right)}^n} - {{\left( {1 - \sqrt 5 } \right)}^n}}}{{{2^n}\sqrt 5 }}\).
a) Chứng tỏ rằng \({u_1} = 1,{u_2} = 1\) và \({u_{n + 2}} = {u_{n + 1}} + {u_n}\) với mọi \(n \in {\mathbb{N}^{\rm{*}}}\).
Từ đó suy ra \(\left( {{u_n}} \right)\) là dãy số Fibonacci.
b) Viết 11 số hạng đầu tiên của dãy Fibonacci và 10 tỉ số \(\frac{{{u_{n + 1}}}}{{{u_n}}}\) đầu tiên.
Tinh \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{u_{n + 1}}}}{{{u_n}}}\).
