Một cây cau có chiều cao 6m. Để hái một buồng cau xuống, phải đặt thang tre sao cho đầu thang đạt độ cao đó. Khi đó góc của thang tre với mặt đất là bao nhiêu độ, biết chiếc thang dài 8m? (làm tròn đến độ)

Đáp án:
Đáp án:
Sử dụng kiến thức về tỉ số lượng giác để tính góc của thang tre với mặt đất.
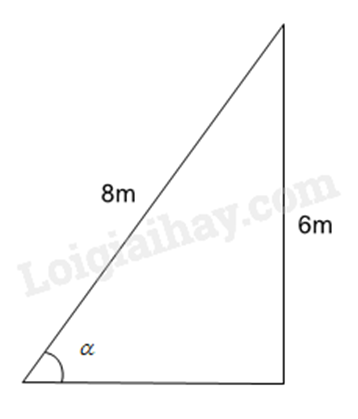
Áp dụng tỉ số lượng giác ta có: \(\sin \alpha = \frac{6}{8} = \frac{3}{4}\) suy ra \(\alpha \approx 49^\circ \)
Vậy góc tạo bởi thang tre với mặt đất khoảng \(49^\circ \).

Các bài tập cùng chuyên đề
Bài 1 :
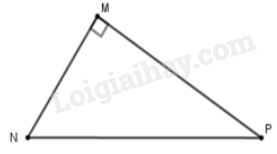
Cho tam giác $MNP$ vuông tại $M$. Khi đó $\cos \widehat {MNP}$ bằng
-
A.
$\dfrac{{MN}}{{NP}}$
-
B.
$\dfrac{{MP}}{{NP}}$
-
C.
$\dfrac{{MN}}{{MP}}$
-
D.
$\dfrac{{MP}}{{MN}}$
Bài 2 :
Cho $\alpha $ là góc nhọn bất kỳ. Chọn khẳng định đúng.
-
A.
$\sin \alpha + \cos \alpha = 1$
-
B.
${\sin ^2}\alpha + {\cos ^2}\alpha = 1$
-
C.
${\sin ^3}\alpha + {\cos ^3}\alpha = 1$
-
D.
$\sin \alpha - cos\alpha = 1$
Bài 3 :
Cho $\alpha $ là góc nhọn bất kỳ. Chọn khẳng định sai.
-
A.
$\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }}\,\,$
-
B.
$\cot \alpha = \dfrac{{\cos \alpha }}{{\sin \alpha }}\,\,$
-
C.
$\tan \alpha .\cot \alpha = 1$
-
D.
${\tan ^2}\alpha - 1 = {\cos ^2}\alpha $
Bài 4 :
Cho tam giác $ABC$ vuông tại $C$ có \(BC = 1,2\,cm,\,\,AC = 0,9\,cm.\) Tính các tỉ số lượng giác $\sin B;\cos B$ .
-
A.
$\sin B = 0,6;\cos B = 0,8$
-
B.
$\sin B = 0,8;\cos B = 0,6$
-
C.
$\sin B = 0,4;\cos B = 0,8$
-
D.
$\sin B = 0,6;\cos B = 0,4$
Bài 5 :
Cho tam giác $ABC$ vuông tại $A$ có \(BC = 8\,cm,\,\,AC = 6cm.\) Tính tỉ số lượng giác $\tan C$ (làm tròn đến chữ số thập phân thứ $2$ ).
-
A.
$\tan C \approx 0,87$
-
B.
$\tan C \approx 0,86$
-
C.
$\tan C \approx 0,88$
-
D.
$\tan C \approx 0,89$
Bài 6 :
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ có \(CH = 4\,cm,\,BH = 3\,cm.\) Tính tỉ số lượng giác $\cos C$ (làm tròn đến chữ số thập phân thứ $2$ )
-
A.
$\cos C \approx 0,76$
-
B.
$\cos C \approx 0,77$
-
C.
$\cos C \approx 0,75$
-
D.
$\cos C \approx 0,78$
Bài 7 :
Cho $\alpha$ là góc nhọn. Tính \(\sin \alpha,\,\cot \alpha \) biết \(\cos \alpha = \dfrac{2}{5}\).
-
A.
$\sin \alpha = \dfrac{{\sqrt {21} }}{{25}};\cot \alpha = \dfrac{{3\sqrt {21} }}{{21}}$
-
B.
$\sin \alpha = \dfrac{{\sqrt {21} }}{5};\cot \alpha = \dfrac{5}{{\sqrt {21} }}$
-
C.
$\sin \alpha = \dfrac{{\sqrt {21} }}{3};\cot \alpha = \dfrac{3}{{\sqrt {21} }}$
-
D.
$\sin \alpha = \dfrac{{\sqrt {21} }}{5};\cot \alpha = \dfrac{2}{{\sqrt {21} }}$
Bài 8 :
Cho $\alpha $ là góc nhọn bất kỳ. Khi đó $C = {\sin ^4}\alpha + {\cos ^4}\alpha $ bằng
-
A.
$C = 1 - 2{\sin ^2}\alpha .{\cos ^2}\alpha $
-
B.
$C = 1$
-
C.
$C = {\sin ^2}\alpha .{\cos ^2}\alpha $
-
D.
$C = 1 + 2{\sin ^2}\alpha .{\cos ^2}\alpha $
Bài 9 :
Cho $\alpha $ là góc nhọn bất kỳ. Rút gọn $P = \left( {1 - {{\sin }^2}\alpha } \right).{\cot ^2}\alpha + 1 - {\cot ^2}\alpha $ ta được
-
A.
$P = {\sin ^2}\alpha $
-
B.
$P = {\cos ^2}\alpha $
-
C.
$P = {\tan ^2}\alpha $
-
D.
$P = 2{\sin ^2}\alpha $
Bài 10 :
Cho $\alpha $ là góc nhọn bất kỳ. Biểu thức $Q = \dfrac{{1 + {{\sin }^2}\alpha }}{{1 - {{\sin }^2}\alpha }}$ bằng
-
A.
$Q = 1 + {\tan ^2}\alpha $
-
B.
$Q = 1 + 2{\tan ^2}\alpha $
-
C.
$Q = 1 - 2{\tan ^2}\alpha $
-
D.
$Q = 2{\tan ^2}\alpha $
Bài 11 :
Cho $\tan \alpha = 2$. Tính giá trị của biểu thức $G = \dfrac{{2\sin \alpha + \cos \alpha }}{{\cos \alpha - 3\sin \alpha }}$
-
A.
$G =1$
-
B.
$G = - \dfrac{4}{5}$
-
C.
$G = - \dfrac{6}{5}$
-
D.
$G = - 1$
Bài 12 :
Cho tam giác nhọn \(ABC\) hai đường cao \(AD\) và \(BE\) cắt nhau tại \(H\). Biết \(HD:HA = 1:2\). Khi đó \(\tan \widehat {ABC}.\tan \widehat {ACB}\) bằng
-
A.
$2$
-
B.
$3$
-
C.
$1$
-
D.
$4$
Bài 13 :
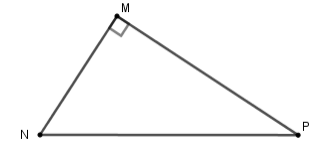
Cho tam giác \(MNP\) vuông tại \(M\). Khi đó \(\tan \widehat {MNP}\) bằng
-
A.
\(\dfrac{{MN}}{{NP}}\)
-
B.
\(\dfrac{{MP}}{{NP}}\)
-
C.
\(\dfrac{{MN}}{{MP}}\)
-
D.
\(\dfrac{{MP}}{{MN}}\)
Bài 14 :
Cho tam giác \(ABC\) vuông tại \(C\) có \(AC = 1\,cm,\,\,BC = 2\,cm.\) Tính các tỉ số lượng giác \(\sin B;\cos B\)
-
A.
\(\sin B = \dfrac{1}{{\sqrt 3 }};\cos B = \dfrac{{2\sqrt 3 }}{3}\)
-
B.
\(\sin B = \dfrac{{\sqrt 5 }}{5};\cos B = \dfrac{{2\sqrt 5 }}{5}\)
-
C.
\(\sin B = \dfrac{1}{2};\cos B = \dfrac{2}{{\sqrt 5 }}\)
-
D.
\(\sin B = \dfrac{{2\sqrt 5 }}{5};\cos B = \dfrac{{\sqrt 5 }}{5}\)
Bài 15 :
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 9\,cm,\,\,AC = 5cm.\) Tính tỉ số lượng giác \(\tan C\) (làm tròn đến chữ số thập phân thứ \(1\) )
-
A.
\(\tan C \approx 0,67\)
-
B.
\(\tan C \approx 0,5\)
-
C.
\(\tan C \approx 1,4\)
-
D.
\(\tan C \approx 1,5\)
Bài 16 :
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\) có \(CH = 11\,cm,\,BH = 12\,cm.\) Tính tỉ số lượng giác \(\cos C\) (làm tròn đến chữ số thập phân thứ \(2\) )
-
A.
\(\cos C \approx 0,79\)
-
B.
\(\cos C \approx 0,69\)
-
C.
\(\cos C \approx 0,96\)
-
D.
\(\cos C \approx 0,66\)
Bài 17 :
Tính \(\sin \alpha ,\,\,\tan \alpha \) biết \(\cos \alpha = \dfrac{3}{4}\).
-
A.
\(\sin \alpha = \dfrac{4}{{\sqrt 7 }};\tan \alpha = \dfrac{{\sqrt 7 }}{3}\)
-
B.
\(\sin \alpha = \dfrac{{\sqrt 7 }}{4};\tan \alpha = \dfrac{3}{{\sqrt 7 }}\)
-
C.
\(\sin \alpha = \dfrac{{\sqrt 7 }}{4};\tan \alpha = \dfrac{{\sqrt 7 }}{3}\)
-
D.
\(\sin \alpha = \dfrac{{\sqrt 7 }}{3};\tan \alpha = \dfrac{{\sqrt 7 }}{4}\)
Bài 18 :
Cho \(\alpha \) là góc nhọn bất kỳ. Khi đó \(C={\sin ^6}\alpha + {\cos ^6}\alpha + 3{\sin ^2}\alpha {\cos ^2}\alpha \) bằng
-
A.
\(C = 1 - 3{\sin ^2}\alpha .{\cos ^2}\alpha \)
-
B.
$C=1$
-
C.
\(C = {\sin ^2}\alpha .{\cos ^2}\alpha \)
-
D.
\(C = 3{\sin ^2}\alpha .{\cos ^2}\alpha - 1\)
Bài 19 :
Cho \(\alpha \) là góc nhọn bất kỳ. Cho \(P = \left( {1 - {{\sin }^2}\alpha } \right).{\tan ^2}\alpha + \left( {1 - {{\cos }^2}\alpha } \right){\cot ^2}\alpha \), chọn kết luận đúng.
-
A.
\(P > 1\)
-
B.
\(P < 1\)
-
C.
\(P = 1\)
-
D.
\(P = 2{\sin ^2}\alpha \)
Bài 20 :
Cho \(\alpha \) là góc nhọn bất kỳ. Biểu thức \(Q = \dfrac{{{{\cos }^2}\alpha - {{\sin }^2}\alpha }}{{\cos \alpha .\sin \alpha }}\) bằng
-
A.
\(Q = \cot \alpha - \tan \alpha \)
-
B.
\(Q = \cot \alpha + \tan \alpha \)
-
C.
\(Q = \tan \alpha - \cot \alpha \)
-
D.
\(Q = 2\tan \alpha \)
Bài 21 :
Cho \(\tan \alpha = 4\). Tính giá trị của biểu thức \(P = \dfrac{{3\sin \alpha - 5\cos \alpha }}{{4\cos \alpha + \sin \alpha }}\)
-
A.
\(P = \dfrac{7}{8}\)
-
B.
\(P = \dfrac{{17}}{8}\)
-
C.
\(P = \dfrac{8}{7}\)
-
D.
\(P = \dfrac{5}{8}\)
Bài 22 :
Cho tam giác nhọn \(ABC\) hai đường cao \(AD\) và \(BE\) cắt nhau tại \(H\). Biết \(HD:HA = 3:2\). Khi đó \(\tan \widehat {ABC}.\tan \widehat {ACB}\) bằng
-
A.
$3$
-
B.
$5$
-
C.
\(\dfrac{3}{5}\)
-
D.
\(\dfrac{5}{3}\)
Bài 23 :
Chọn kết luận đúng về giá trị biểu thức \(B = \dfrac{{{{\cos }^2}\alpha - 3{{\sin }^2}\alpha }}{{3 - {{\sin }^2}\alpha }}\) biết \(\tan \alpha = 3.\)
-
A.
\(B > 0\)
-
B.
\(B < 0\)
-
C.
\(0 < B < 1\)
-
D.
\(B = 1\)
Bài 24 :
Cho tam giác \(ABC\) cân tại \(A\) có \(AB = AC = 13cm\); \(BC = 10cm\). Tính \(sinA\).
-
A.
\(\sin A = \dfrac{{120}}{{169}}\)
-
B.
\(\sin A = \dfrac{{60}}{{169}}\)
-
C.
\(\sin A = \dfrac{5}{6}\)
-
D.
\(\sin A = \dfrac{{10}}{{13}}\)
Bài 25 :
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 3,AB = 4\). Khi đó \(\cos B\) bằng
-
A.
\(\dfrac{3}{4}\)
-
B.
\(\dfrac{3}{5}\)
-
C.
\(\dfrac{4}{3}\)
-
D.
\(\dfrac{4}{5}\)
Bài 26 :
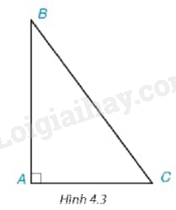
Xét góc C của tam giác ABC vuông tại A (H.4.3) . Hãy chỉ ra cạnh đối và cạnh kề của góc C.
Bài 27 :
Cho tam giác ABC vuông tại A và tam giác A’B’C’ vuông tại A’ có \(\widehat B = \widehat {B'} = \alpha .\) Chứng minh rằng:
a) \(\Delta ABC\backsim \Delta A'B'C';\)
b) \(\frac{{AC}}{{BC}} = \frac{{A'C'}}{{B'C'}};\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}};\frac{{AC}}{{AB}} = \frac{{A'C'}}{{A'B'}};\frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}}\)
Bài 28 :
Cho tam giác ABC vuông tại A có AB = 5 cm, AC = 12 cm. Hãy tính các tỉ số lượng giác của góc B.
Bài 29 :
Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác sin, cosin, tang, cotang của các góc nhọn B và C khi biết:
a) AB = 8 cm, BC = 17 cm;
b) AC = 0,9 cm, AB = 1,2 cm.
Bài 30 :
Trong Hình 4.32, \(\cos \alpha \) bằng
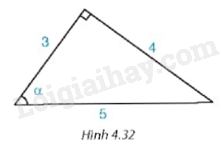
A. \(\frac{5}{3}.\)
B. \(\frac{3}{4}.\)
C. \(\frac{3}{5}.\)
D. \(\frac{4}{5}.\)


















Danh sách bình luận