Đề bài

Một con lắc đơn được treo ở trần một thang máy. Khi thang máy đứng yên, con lắc dao động điều hoà với chu kì T. Khi thang máy đi lên thẳng đứng, chậm dần đều với gia tốc có độ lớn bằng một nửa gia tốc trọng trường tại nơi đặt thang máy thì con lắc dao động điều hoà với chu kì T’ bằng:

• A. 2T
• B. \(\sqrt 2 T\)
• C. \(\frac{T}{2}\)
• D. \(\frac{T}{{\sqrt 2 }}\)

Phương pháp giải

+ Áp dụng công thức tính chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\frac{l}{g}} \)

+ Áp dụng bài toán con lắc đơn chịu thêm tác dụng của lực quán tính

Lời giải của GV Loigiaihay.com

Ta có:

+ Khi thang máy đứng yên: \(T = 2\pi \sqrt {\frac{l}{g}} \)

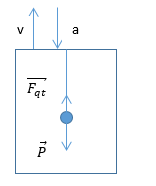
+ Khi thang máy đi lên chậm dần đều => v hướng lên, a hướng xuống, F_qt hướng lên

Chu kì dao động của con lắc khi đó:

\(T' = 2\pi \sqrt {\frac{l}{{g'}}} \)

 \(\begin{array}{l}g' = g - a = g - \frac{g}{2} = \frac{g}{2}\\ \to T' = 2\pi \sqrt {\frac{{2l}}{g}}  = \sqrt 2 T\end{array}\)

Đáp án : B