Mệnh đề nào sau đây sai?
A. Hàm số \(y = \sin x\cos 2x\) là hàm số tuần hoàn.
B. Hàm số \(y = \sin x\cos 2x\) là hàm số lẻ.
C. Hàm số \(y = x\sin x\) là hàm số tuần hoàn.
D. Hàm số \(y = x\sin x\) là hàm số chẵn.
Xét tính chẵn lẻ
Bước 1: Tìm tập xác định của hàm số, xét xem với mọi \(x \in D\), \( - x \in D\) hay không.
Bước 2: Xét \(f( - x)\)
+) Nếu \(f( - x) = f(x)\) thì đó là hàm số chẵn.
+) Nếu \(f( - x) = - f(x)\) thì đó là hàm số lẻ.
+) Nếu không rơi vào 2 trường hợp trên thì đó là hàm số không chẵn không lẻ.
Xét tính tuần hoàn
Bước 1: Tập xác định D.
Bước 2: Chứng minh rằng với mọi \(x \in D\), \(x + T \in D\)và \(f(x + T) = f(x)\).
Nếu không tồn tại số T khác không thỏa mãn điều kiện trên, ta kết luận hàm số không tuần hoàn.
Đáp án C.
Với hàm \(f(x) = x\sin x\), \(f(x + T) = (x + T)\sin (x + T)\).
\(f(x + T) = f(x) \Leftrightarrow (x + T)\sin (x + T) = x\sin x \Leftrightarrow T = 0\)
Ta không tìm được số T (khác 0) nào để \(f(x + T) = f(x)\forall x\). Vậy đây không phải là hàm tuần hoàn.
Các bài tập cùng chuyên đề
Xét tính tuần hoàn của hàm số \(y = \tan 2x\).
So sánh:
a) \(\sin \left( {x + 2\pi } \right)\) và \(\sin x\);
b) \(\cos (x + 2\pi )\) và \(\cos x\);
c) \(\tan \left( {x + \pi } \right)\) và \(\tan x\);
d) \(\cot (x + \pi )\) và \(\cot x\).
Xét tính chẵn, lẻ của hàm số \(g\left( x \right) = \frac{1}{x}\).
Cho hai hàm số \(f\left( x \right) = {x^2}\) và \(g\left( x \right) = {x^3}\), với các đồ thị như hình dưới đây.
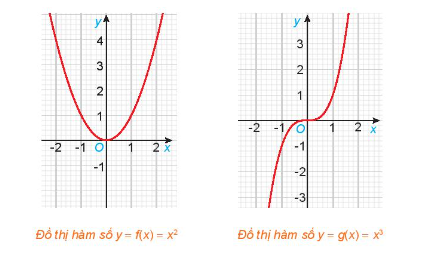
a) Tìm các tập xác định \({D_f},\;{D_g}\) của các hàm số \(f\left( x \right)\) và \(g\left( x \right)\).
b) Chứng tỏ rằng \(f\left( { - x} \right) = f\left( x \right),\;\forall x \in {D_f}\). Có nhận xét gì về tính đối xứng của đồ thị hàm số \(y = f\left( x \right)\) đối với hệ trục tọa độ Oxy?
c) Chứng tỏ rằng \(g\left( { - x} \right) = - g\left( x \right),\;\forall x \in {D_g}\). Có nhận xét gì về tính đối xứng của đồ thị hàm số \(y = g\left( x \right)\) đối với hệ trục tọa độ Oxy?
Xét tính chẵn lẻ của các hàm số sau:
a) \(y = \sin 2x + \tan 2x\);
b) \(y = \cos x + {\sin ^2}x\);
c) \(y = \sin x\cos 2x\);
d) \(y = \sin x + \cos x\).
Trong các hàm số sau đây, hàm số nào là hàm tuần hoàn?
A. \(y = \tan x + x\)
B. \(y = {x^2} + 1\)
C. \(y = \cot x\)
D. \(y = \frac{{\sin x}}{x}\)
Cho ví dụ về hàm số tuần hoàn
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) và có đồ thị như Hình 22.
a) Có nhận xét gì về đồ thị hàm số trên mỗi đoạn \(\left[ {a;a + T} \right],\left[ {a + T;a + 2T} \right],\left[ {a - T;a} \right]\)?
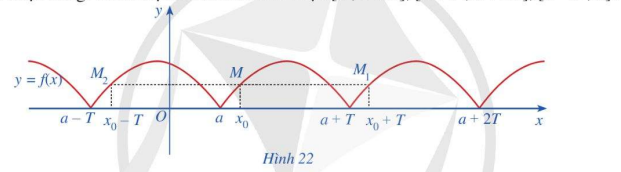
b) Lấy điểm \(M\left( {{x_0};f\left( {{x_0}} \right)} \right)\) thuộc đồ thị hàm số với \({x_0} \in \left[ {a;a + T} \right]\). So sánh mỗi giá trị \(f\left( {{x_0} + T} \right);f\left( {{x_0} - T} \right)\) với \(f\left( {{x_0}} \right)\)
a) Chứng tỏ rằng hàm số \(g(x) = {x^3}\)là hàm số lẻ.
b) Cho ví dụ về hàm số không là hàm số chẵn cũng không là hàm số lẻ.
a) Cho hàm số \(f\left( x \right) = {x^2}\)
Với \(x \in \mathbb{R}\), hãy so sánh \(f\left( { - x} \right)\) và \(f\left( x \right)\)
Quan sát parabol (P) là đồ thị của hàm số \(f\left( x \right) = {x^2}\) (Hình 20) và cho biết trục đối xứng của (P) là đường thẳng nào?
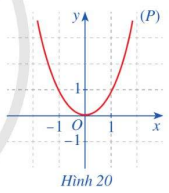
b) Cho hàm số \(g\left( x \right) = x\)
Với \(x \in \mathbb{R}\), hãy so sánh \(g\left( { - x} \right)\) và \(g\left( x \right)\)
Quan sát đường thẳng d là đồ thị của hàm số \(g\left( x \right) = x\) (Hình 21) và cho biết gốc tọa độ O có là tâm đối xứng của đường thẳng d hãy không.
Xét tính chẵn, lẻ của các hàm số:
a) \(y = \sin x\cos x\)
b) \(y = \tan x + \cot x\)
c) \(y = {\sin ^2}x\)
Xét tính tuần hoàn của hàm số y = cosx và hàm số y = cotx
Hãy chỉ ra một số thực T sao cho sin(x + T) = sinx với mọi \(x \in \mathbb{R}\).
Chứng minh rằng hàm số y = sinx và hàm số y = cotx là các hàm số lẻ.
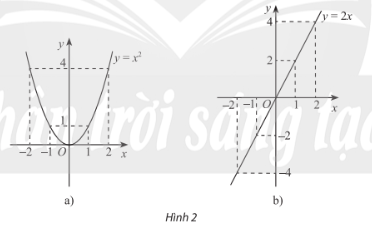
Xét hai hàm số \(y = {x^2},y = 2x\) và đồ thị của chúng trong Hình 2. Đối với mỗi trường hợp, nêu mối liên hệ của giá trị hàm số tại 1 và -1, 2 và -2. Nhận xét về tính đối xứng của mỗi đồ thị hàm số.
a, \(y = 5si{n^2}\alpha + 1\)
b, \(y = cosx + sinx\)
c, \(y = tan2x\)
Khẳng định nào sau đây là đúng?
A. Hàm số y = sinx là hàm số chẵn.
B. Hàm số y = cosx là hàm số chẵn
C. Hàm số y = tanx là hàm số chẵn
D. Hàm số y = cotx là hàm số chẵn
Hàm số nào sau đây là hàm số chẵn?
Hàm số nào sau đây là hàm số chẵn?
Khẳng định nào sau đây là sai?
Hàm số \(y = f\left( x \right)\) (có tập xác định \(D\)) là hàm số lẻ nếu với \(\forall x \in D\) thì \( - x \in D\) và
Hàm số \(y = f\left( x \right)\) có tập xác định \(D\) là hàm số tuần hoàn nếu tồn tại một số \(T\) khác \(0\) sao cho \(\forall x \in D\) ta có \(x + T \in D,x - T \in D\) và
Xét tính chẵn lẻ của các hàm số sau:
a) \(y = \frac{{\cos 2x}}{{{x^3}}}\);
b) \(y = x - \sin 3x\);
c) \(y = \sqrt {1 + \cos x} \);
d) \(y = 1 + \cos x\sin \left( {\frac{{3\pi }}{2} - 2x} \right)\).
Xét tính tuần hoàn của các hàm số sau:
a) \(y = {\rm{A}}\sin \left( {\omega x + \varphi } \right)\) với A > 0;
b) \(y = {\rm{A}}\tan \left( {\omega x + \varphi } \right)\) với A > 0;
c) \(y = 3\sin 2x + 3\cos 2x\);
d) \(y = 3\sin \left( {2x + \frac{\pi }{6}} \right) + 3\sin \left( {2x - \frac{\pi }{3}} \right)\).
Mệnh đề nào sau đây sai?
A. Hàm số \(y = \sin x\) tuần hoàn với chu kì \(2\pi \).
B. Hàm số \(y = \cos x\) tuần hoàn với chu kì \(2\pi \).
C. Hàm số \(y = \tan x\) tuần hoàn với chu kì \(2\pi \).
D. Hàm số \(y = \cot x\) tuần hoàn với chu kì \(\pi \).
Xét tính chẵn lẻ của các hàm số sau:
a) \(y = {\sin ^3}x - \cot x;\)
b) \(y = \frac{{\cos x + {{\tan }^2}x}}{{\cos x}}\);
c) \(y = \sin 2x + \cos x\);
d) \(y = 2\cos \left( {\frac{{3\pi }}{4} + x} \right)\sin \left( {\frac{\pi }{4} - x} \right)\).
Xét tính tuần hoàn của các hàm số sau:
a) \(y = \sin \frac{x}{2} + \cos 3x\);
b) \(y = \cos 5x + \tan \frac{x}{3}\).
Hàm số nào sau đây là hàm số lẻ?
A. \(y = - 2\cos x\)
B. \(y = - 2\sin x\)
C. \(y = \tan x - \cos x\)
D. \(y = - 2\sin x + 2\)
Hàm số nào sau đây là hàm số chẵn?
A. \(y = \cos x + 5\)
B. \(y = \tan x + \cot x\)
C. \(y = \sin \left( { - x} \right)\)
D. \(y = \sin x - \cos x\)
Xét tính chẵn, lẻ của các hàm số sau:
a) \(y = \sin 2x\)
b) \(y = \left| {\sin x} \right|\)
c) \(y = {\tan ^2}x\)
d) \(y = \sqrt {1 - \cos x} \)
e) \(y = \tan x + \cot x\)
f) \(y = \sin x\cos 3x\)
