Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right)\) xác định trên \(\mathbb{R}\) và \(f'\left( x \right)\) có đồ thị như hình vẽ sau:
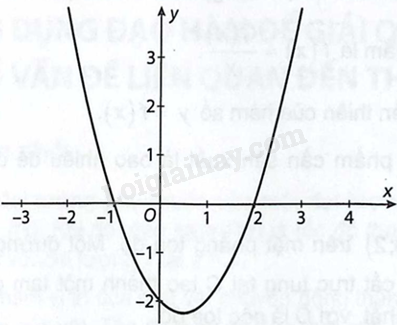
Tìm các khoảng đồng biến, khoảng nghịch biến và các điểm cực trị của hàm số \(y = f\left( x \right)\).
+ Từ đồ thị của đạo hàm tìm \(x\) để đạo hàm bằng \(0\) (các giao điểm của đồ thị và trục
hoành).
+ Xét dấu đạo hàm (quan sát đồ thị, phần đồ thị phía trên trục hoành nhận giá trị dương, dưới trục hoành nhận giá trị âm, xác định các khoảng của x thỏa mãn từng phần). Từ đó xác định các khoảng đồng biến, nghịch biến.
+ Lập bảng biến thiên. Từ bảng biến thiên suy ra cực trị.
Từ đồ thị của hàm \(f'\left( x \right)\) ta có \(f'\left( x \right) = 0 \Leftrightarrow x = - 1\) hoặc \(x = 2\).
Ta có \(f'\left( x \right) > 0\) với mọi \(x \in \left( { - \infty ; - 1} \right)\) và \(x \in \left( {2; + \infty } \right)\) do đó \(f\left( x \right)\) đồng biến trên từng khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {2; + \infty } \right)\); \(f'\left( x \right) < 0\) với mọi \(x \in \left( { - 1;2} \right)\) do đó \(f\left( x \right)\) nghịch biến trên \(\left( { - 1;2} \right)\).
Lập bảng biến thiên
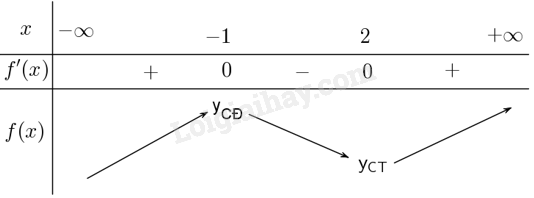
Hàm số đạt cực đại tại \(x = - 1\), đạt cực tiểu tại \(x = 2\).

Các bài tập cùng chuyên đề
Bài 1 :
Hình dưới là đồ thị hàm số \(y = f'\left( x \right)\). Hỏi hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
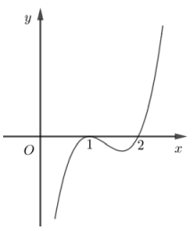
-
A.
\(\left( {0;1} \right)\) và \(\left( {2; + \infty } \right)\)
-
B.
\(\left( {1;2} \right)\)
-
C.
\(\left( {2; + \infty } \right)\)
-
D.
\(\left( {0;1} \right)\)
Bài 2 :
Trong tất cả các giá trị của tham số $m$ để hàm số $y = \dfrac{1}{3}{x^3} + m{x^2} - mx - m$ đồng biến trên $R$, giá trị nhỏ nhất của $m$ là:
-
A.
$ - 4$
-
B.
$ - 1$
-
C.
$0$
-
D.
$1$
Bài 3 :
Tìm $m$ để hàm số $y = \dfrac{{{x^3}}}{3} - 2m{x^2} + 4mx + 2$ nghịch biến trên khoảng $\left( { - 2;0} \right)$.
-
A.
$m < - \dfrac{1}{3}$
-
B.
$m \leqslant - \dfrac{1}{3}$
-
C.
$m \leqslant - \dfrac{4}{3}$
-
D.
$m \leqslant 0$
Bài 4 :
Cho bảng biến thiên hình bên, hàm số nghịch biến trên:
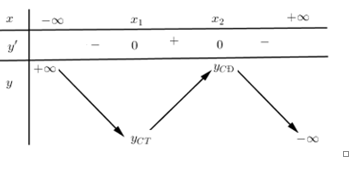
-
A.
$\left( {{x_1};{x_2}} \right)$
-
B.
$\left( { - \infty ;{x_1}} \right)$
-
C.
$\left( {{x_1}; + \infty } \right)$
-
D.
$\left( { - \infty ;{x_2}} \right)$
Bài 5 :
Hình bên là đồ thị hàm số \(y = f'\left( x \right)\) Hỏi hàm số \(y = f\left( x \right)\) nghịch biến trên khoảng nào dưới đây?
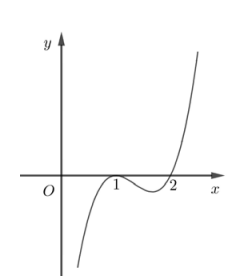
-
A.
\(\left( {2;3} \right)\)
-
B.
\(\left( {1; + \infty } \right)\)
-
C.
\(\left( {2; + \infty } \right)\)
-
D.
\(\left( { - \infty ;2} \right)\)
Bài 6 :
Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y = mx - \sin x$ đồng biến trên $\mathbb{R}.$
-
A.
$m > 1.$
-
B.
$m \le - 1.$
-
C.
$m \ge 1.$
-
D.
$m \ge - 1.$
Bài 7 :
Tìm tất cả các giá trị của tham số m để hàm số $y = {x^3} + {x^2} + mx + 1$ đồng biến trên khoảng $\left( { - \infty ; + \infty } \right)$
-
A.
$m \geqslant \dfrac{4}{3}$
-
B.
$m \leqslant \dfrac{4}{3}$
-
C.
$m \geqslant \dfrac{1}{3}$
-
D.
$m \leqslant \dfrac{1}{3}$
Bài 8 :
Tập hợp tất cả các giá trị của m để hàm số $y = \dfrac{1}{3}{x^3} - \left( {m - 1} \right){x^2} + 2\left( {m - 1} \right)x - 2$ luôn tăng trên $R$
-
A.
$m > 1$
-
B.
$\left[ {\begin{array}{*{20}{l}}{m < 1}\\{m > 3}\end{array}} \right.$
-
C.
$2 \le m \le 3$
-
D.
$1 \le m \le 3$
Bài 9 :
Tìm $m$ để hàm số $y = {x^3} - 3{x^2} + mx + 2$ tăng trên khoảng $\left( {1; + \infty {\rm{\;}}} \right).$
-
A.
$m \ge 3.$
-
B.
$m \ne 3.$
-
C.
$m \le 3.$
-
D.
$m < 3.$
Bài 10 :
Hàm số $y = {x^3} - 6{x^2} + mx + 1$ đồng biến trên $\left( {0; + \infty {\rm{\;}}} \right)$ khi giá trị của $m$ là:
-
A.
$m \ge 12$
-
B.
$m \le 12$
-
C.
$m \ge 0$
-
D.
$m \le 0$
Bài 11 :
Tìm các giá trị của tham số $m$ để hàm số $y = - {\mkern 1mu} {x^3} + m{x^2} - m$ đồng biến trên khoảng $\left( {1;2} \right).$
-
A.
$\left( {\dfrac{3}{2};3} \right).$
-
B.
$\left( { - {\mkern 1mu} \infty ;\dfrac{3}{2}} \right).$
-
C.
$\left[ {3; + {\mkern 1mu} \infty } \right).$
-
D.
$\left( { - {\mkern 1mu} \infty ;3} \right].$
Bài 12 :
Cho bảng biến thiên hình bên, hàm số đồng biến trên:
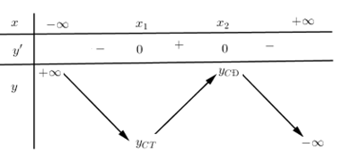
-
A.
\(\left( {{x_1};{x_2}} \right)\)
-
B.
\(\left( { - \infty ;{x_1}} \right)\)
-
C.
\(\left( {{x_1}; + \infty } \right)\)
-
D.
\(\left( { - \infty ;{x_2}} \right)\)
Bài 13 :
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?

-
A.
\(\left( {0;1} \right)\)
-
B.
\(\left( { - \infty ; - 1} \right)\)
-
C.
\(\left( { - 1;1} \right)\)
-
D.
\(\left( { - 1;0} \right)\)
Bài 14 :
Tập hợp tất cả các giá trị thực của tham số m để hàm số \(y = - {x^3} - 6{x^2} + \left( {4m - 9} \right)x + 4\) nghịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\) là:
-
A.
\(\left( { - \infty ;0} \right]\)
-
B.
\(\left[ { - \dfrac{3}{4}; + \infty } \right)\)
-
C.
\(\left( { - \infty ; - \dfrac{3}{4}} \right]\)
-
D.
\(\left[ {0; + \infty } \right)\)
Bài 15 :
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Hàm số \(y = f\left( x \right)\) nghịch biến trên khoảng nào trong các khoảng sau?
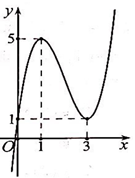
-
A.
\(\left( {0;1} \right)\).
-
B.
\(\left( {1;5} \right)\).
-
C.
\(\left( {3; + \infty } \right)\).
-
D.
\(\left( {1;2} \right)\).
Bài 16 :
Tập tất cả giá trị của tham số \(m\) để hàm số \(y = {x^3} - 3m{x^2} + 3x + 1\) đồng biến trên \(\mathbb{R}\) là
-
A.
\(\left[ { - 1;\,1} \right]\).
-
B.
\(m \in \left( { - \infty ;\, - 1} \right] \cup \left[ {1;\, + \infty } \right)\).
-
C.
\(\left( { - \infty ;\, - 1} \right) \cup \left( {1;\, + \infty } \right)\).
-
D.
\(\left( { - 1;\,1} \right)\).
Bài 17 :
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên.
Hàm số đã cho nghịch biến trên khoảng:
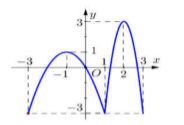
-
A.
\(\left( {0;\,\,2} \right)\)
-
B.
\(\left( { - 2;\,0} \right)\)
-
C.
\(\left( { - 3; - 1} \right)\)
-
D.
\(\left( {2;\,3} \right)\)
Bài 18 :
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên:

Hàm số \(y = - 2f\left( x \right)\) đồng biến trên khoảng
-
A.
\(\left( {1;2} \right)\)
-
B.
\(\left( {2;3} \right)\)
-
C.
\(\left( { - 1;0} \right)\)
-
D.
\(\left( { - 1;1} \right)\)
Bài 19 :
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu \(f'\left( x \right)\) như sau:

Hàm số \(y = f\left( {2 - 3x} \right)\) đồng biến trên khoảng nào sau đây?
-
A.
\(\left( {1;3} \right)\)
-
B.
\(\left( {1;2} \right)\)
-
C.
\(\left( {2;3} \right)\)
-
D.
\(\left( {0;1} \right)\)
Bài 20 :
Tập tất cả các giá trị của tham số \(m\) để hàm số \(y = \dfrac{1}{3}{x^3} + 2{x^2} - mx\) đồng biến trên \(\mathbb{R}\) là:
-
A.
\(\left( { - 4; + \infty } \right)\)
-
B.
\(\left[ { - 4; + \infty } \right)\)
-
C.
\(\left( { - \infty ; - 4} \right)\)
-
D.
\(\left( { - \infty ; - 4} \right]\)
Bài 21 :
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ sau. Hàm số đã cho nghịch biến trên khoảng:
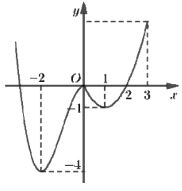
-
A.
\(\left( { - 1;\,\,0} \right)\)
-
B.
\(\left( { - 2; - 1} \right)\)
-
C.
\(\left( {0;\,\,1} \right)\)
-
D.
\(\left( {1;\,\,3} \right)\)
Bài 22 :
Đề thi THPT QG - 2021 - mã 101
Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
-
A.
\(\left( {0;1} \right)\)
-
B.
\(\left( { - \infty ;0} \right)\)
-
C.
\(\left( {0; + \infty } \right)\)
-
D.
\(\left( { - 1;1} \right)\)
Bài 23 :
Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
-
A.
\(\left( { - \infty ;2} \right)\)
-
B.
\(\left( {0;2} \right)\)
-
C.
\(\left( { - 2;2} \right)\)
-
D.
\(\left( {2; + \infty } \right)\)
Bài 24 :
Đề thi THPT QG - 2021 - mã 102
Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
-
A.
\(\left( { - 1;1} \right)\)
-
B.
\(\left( { - \infty ;0} \right)\)
-
C.
\(\left( {0;1} \right)\)
-
D.
\(\left( {0; + \infty } \right)\)
Bài 25 :
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
-
A.
\(\left( { - 1;1} \right)\)
-
B.
\(\left( {1; + \infty } \right)\)
-
C.
\(\left( { - \infty ;1} \right)\)
-
D.
\(\left( {0;3} \right)\)
Bài 26 :
Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số \(y = {x^3} - 3\left( {2m + 1} \right){x^2} + \left( {12m + 5} \right)x + 2\) đồng biến trên khoảng \(\left( {2; + \infty } \right).\) Số phần tử của \(S\) bằng:
-
A.
\(1\)
-
B.
\(2\)
-
C.
\(3\)
-
D.
\(0\)
Bài 27 :
Quan sát đồ thị của hàm số \(y = {x^3} + 3{x^2} - 4\) (H.1.7). Xét dấu đạo hàm của hàm số đã cho và hoàn thành các bảng sau vào vở:
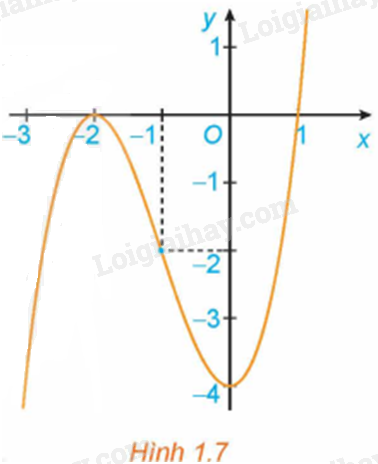
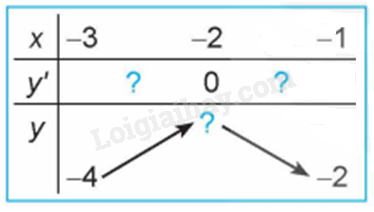
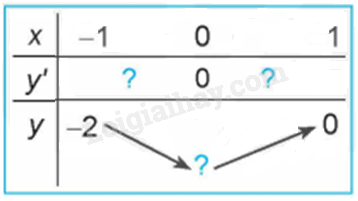
Bài 28 :
Xét sự đồng biến, nghịch biến của các hàm số sau:
a) \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x + 1\);
b) \(y = - {x^3} + 2{x^2} - 5x + 3\).
Bài 29 :
Tìm các khoảng đơn điệu của các hàm số sau:
a) \(y = \frac{{2x - 1}}{{x + 2}}\);
b) \(y = \frac{{{x^2} + x + 4}}{{x - 3}}\).
Bài 30 :
Xét chiều biến thiên của các hàm số sau:
a) \(y = \sqrt {4 - {x^2}} \);
b) \(y = \frac{x}{{{x^2} + 1}}\).

















