Cho hai đường tròn (O; R) và (O; 2R). Một dây cung AB của đường tròn (O; 2R) tiếp xúc với đường tròn (O; R) tại M. Kẻ tiếp tuyến thứ hai AN của đường tròn (O; R). Gọi S1 là diện tích của hình tạo bởi cung ACB và dây AB của đường tròn (O; 2R), S2 là diện tích của hình tạo bởi hai tiếp tuyến AM, AN và cung nhỏ MN của đường tròn (O; R) và S3 là diện tích của hình tròn (O; R) (Hình 45). Chứng minh S1 + S2 = S3.
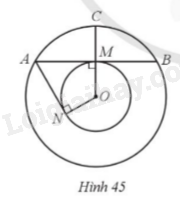
Bước 1: Tính AM và góc AOM.
Bước 2: Tính AB và góc AOB (dựa vào \(\Delta OAM = \Delta OBM\)).
Bước 3: Tính góc MON.
Bước 4: Tính S1 = diện tích quạt tròn AOB – diện tích tam giác OAB.
Bước 5: Tính S2 = diện tích tam giác OAM + diện tích tam giác \(\Delta OAN\) - diện tích quạt tròn OMN.
Bước 5: Tính S1 + S2 rồi so sánh với S3.
Vì AB tiếp xúc với (O;R) tại M nên AB là tiếp tuyến của (O;R), do đó \(OC \bot AB\) tại M hay \(\widehat {AMO} = \widehat {BMO} = 90^\circ \).
Áp dụng định lý Pythagore trong tam giác AMO vuông tại M có \(AM = \sqrt {A{O^2} - M{O^2}} = \sqrt {{{\left( {2R} \right)}^2} - {R^2}} = R\sqrt 3 \)
Ta lại có \(\cos \widehat {AOM} = \frac{{OM}}{{OA}} = \frac{R}{{2R}} = \frac{1}{2}\) suy ra \(\widehat {AOM} = 60^\circ \).
Xét tam giác OAM và tam giác OBM có:
\(OA = OB\left( { = 2R} \right)\);
OM chung;
\(\widehat {AMO} = \widehat {BMO} = 90^\circ \)
Suy ra \(\Delta OAM = \Delta OBM\) (cạnh huyền – cạnh góc vuông)
Do đó \(AM = BM = \frac{{AB}}{2}\) và \(\widehat {AOM} = \widehat {BOM} = \frac{{\widehat {AOB}}}{2}\)
Suy ra \(AB = 2AM = 2R\sqrt 3 \) và \(\widehat {AOB} = 2\widehat {AOM} = 2.60^\circ = 120^\circ \).
Do AM, AN là 2 tiếp tuyến của (O;R) nên \(\widehat {AOM} = \widehat {AON} = \frac{{\widehat {MON}}}{2}\) hay \(\widehat {MON} = 2\widehat {AOM} = 2.60^\circ = 120^\circ \).
Xét tam giác OMA và tam giác ONA có:
OA chung;
\(OM = ON\left( { = R} \right)\);
\(AM = AN\) (tính chất 2 tiếp tuyến cắt nhau)
Suy ra \(\Delta OAM = \Delta OAN\)(c.c.c), nên \({S_{\Delta OAM}} = {S_{\Delta OAN}}\)
Ta có: S1 = diện tích quạt tròn AOB – diện tích \(\Delta OAB\)
Hay \({S_1} = \frac{{\pi {{\left( {2R} \right)}^2}n}}{{360}} - \frac{{OM.AB}}{2}\)\( = \frac{{\pi 4{R^2}.120}}{{360}} - \frac{{R.2R\sqrt 3 }}{2}\)\( = {R^2}\left( {\frac{{4\pi }}{3} - \sqrt 3 } \right)\)
S2 = diện tích \(\Delta OAM\) + diện tích tam giác \(\Delta OAN\) - diện tích quạt tròn OMN
Hay S2 = 2. diện tích \(\Delta OAM\) - diện tích quạt tròn OMN
Do đó \({S_2} = 2.\frac{{AM.OM}}{2} - \frac{{\pi {R^2}.n}}{{360}}\)\( = 2.\frac{{R\sqrt 3 .R}}{2} - \frac{{\pi {R^2}.120^\circ }}{{360}}\)\( = {R^2}\left( {\sqrt 3 - \frac{\pi }{3}} \right)\)
S3 = diện tích hình tròn (O;R) \( = \pi {R^2}\)
Ta có \({S_1} + {S_2} = {R^2}\left( {\frac{{4\pi }}{3} - \sqrt 3 } \right) + {R^2}\left( {\sqrt 3 - \frac{\pi }{3}} \right) = \pi {R^2} = {S_3}\) (đpcm)

Các bài tập cùng chuyên đề
Bài 1 :
Cho đường tròn $\left( {O,10\,cm} \right)$, đường kính $AB.$. Điểm \(M \in (O)\) sao cho \(\widehat {BAM} = {45^0}\). Tính diện tích hình quạt $AOM$ .
-
A.
\(5\pi (c{m^2})\)
-
B.
\(25\pi (c{m^2})\)
-
C.
\(50\pi (c{m^2})\)
-
D.
\(\dfrac{{25}}{2}\pi (c{m^2})\)
Bài 2 :
Cho đường tròn $\left( O \right)$ đường kính $AB = $ \(4\sqrt 3 \) $cm$ .
Điểm \(C \in (O)\) sao cho \(\widehat {ABC} = {30^0}\). Tính diện tích hình viên phân$AC$ . (Hình viên phân là phần hình tròn giới hạn bởi một cung tròn và dây căng cung ấy).
-
A.
\(\pi - 3\sqrt 3 \) $ cm^2$
-
B.
\(2\pi - 3\sqrt 3 \) $ cm^2$
-
C.
\(4\pi - 3\sqrt 3 \) $ cm^2$
-
D.
\(2\pi - \sqrt 3 \) $ cm^2$
Bài 3 :
Cho đường tròn $\left( O \right)$ đường kính \(AB = 2\sqrt 2 \;cm\). Điểm \(C \in (O)\) sao cho \(\widehat {ABC} = {30^0}\). Tính diện tích hình giới hạn bởi đường tròn $\left( O \right)$ và $AC,BC$ .
-
A.
\(\pi - \sqrt 3 \)
-
B.
\(2\pi - 2\sqrt 3 \)
-
C.
\(\pi - 3\sqrt 3 \)
-
D.
\(2\pi - \sqrt 3 \)
Bài 4 :
Cho hình vuông \(ABCD\) có cạnh \(2R.\)
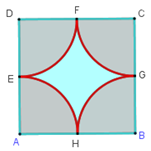
Diện tích \(S\) phần màu xanh trong hình vuông \(ABCD\) là
-
A.
\(S = 4{R^2} - \pi {R^2}\)
-
B.
\(S = \pi {R^2} - {R^2}\)
-
C.
\(S = 4{R^2} + \pi {R^2}\)
-
D.
\(S = 4\pi {R^2}\)
Bài 5 :
Cho đường tròn $\left( {O,8\,cm} \right)$, đường kính $AB.$ Điểm \(M \in (O)\) sao cho \(\widehat {BAM} = {60^0}\). Tính diện tích hình quạt $AOM$ .
-
A.
\(32\pi (c{m^2})\)
-
B.
\(\dfrac{{16\pi }}{3}(c{m^2})\)
-
C.
\(\dfrac{{32\pi }}{3}(c{m^2})\)
-
D.
\(23\pi (c{m^2})\)
Bài 6 :
Cho đường tròn $\left( O \right)$ đường kính $AB = $ $3\sqrt 3 $$cm$ . Điểm \(C \in (O)\) sao cho \(\widehat {ABC} = {60^0}\). Tính diện tích hình viên phân$BC$ . (Hình viên phân là phần hình tròn giới hạn bởi một cung tròn và dây căng cung ấy)
-
A.
$\dfrac{{18\pi - 27\sqrt 3 }}{{16}}\left( {c{m^2}} \right)$
-
B.
$\dfrac{{18\pi - 9\sqrt 3 }}{{16}}\left( {c{m^2}} \right)$
-
C.
$\dfrac{{2\pi - 3\sqrt 3 }}{{16}}\left( {c{m^2}} \right)$
-
D.
$\dfrac{{18\pi - 27\sqrt 3 }}{4}\left( {c{m^2}} \right)$
Bài 7 :
Cho đường tròn $\left( O \right)$ đường kính \(AB = 4\sqrt 2 \;cm\). Điểm \(C \in (O)\) sao cho \(\widehat {ABC} = {30^0}\). Tính diện tích hai hình viên phân giới hạn bởi nửa đường tròn $\left( O \right)$ và dây $AC,BC$ .
-
A.
\(\pi - \sqrt 3 \)
-
B.
\(2\pi - 2\sqrt 3 \)
-
C.
\(\pi - 3\sqrt 3 \)
-
D.
\(2\pi - \sqrt 3 \)
Bài 8 :
Biết rằng hai hình quạt tròn ứng với hai cung bằng nhau trên một đường tròn thì có diện tích bằng nhau và diện tích quạt tròn tỉ lệ với số đo của cung tương ứng với nó. Hãy thiết lập công thức tính diện tích hình quạt tròn bán kính R với cung \(n^\circ \) bằng cách thực hiện từng bước sau:
a) Tính diện tích hình quạt tròn ứng với cung \(1^\circ .\)
b) Tính diện tích hình quạt tròn ứng với cung \(n^\circ .\)
Bài 9 :
Trở lại tình huống mở đầu. Hãy vẽ (tô màu) hình quạt tròn theo hướng dẫn sau:
- Vẽ đường tròn tâm O (với bán kính tùy chọn).
- Hình quạt tròn cần vẽ ứng với cung có số đo bằng 40% của 3600. Tính số đo của cung cần vẽ.
- Vẽ góc ở tâm có số đo tìm được và tô màu hình quạt tròn tương ứng.
Bài 10 :
Tính diện tích của hình quạt tròn đã vẽ trong Thực hành trên nếu bán kính của nó bằng 4cm.
Bài 11 :
Tính diện tích của hình quạt tròn bán kính 4 cm, ứng với cung \(36^\circ .\)
Bài 12 :
Có hai chiếc bánh pizza hình tròn (H.5.18). Chiếc bánh thứ nhất có đường kính 16 cm được cắt thành 6 miếng đều nhau có dạng hình quạt tròn. Chiếc bánh thứ hai có đường kính 18 cm được cắt thành 8 miếng đều nhau có dạng hình quạt tròn. Hãy so sánh diện tích bề mặt của hai miếng bánh cắt ra từ chiếc bánh thứ nhất và thứ hai.

Bài 13 :
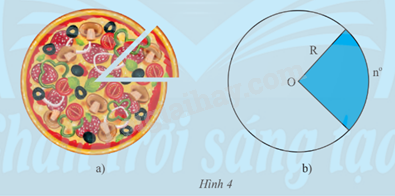
a) Ta có thể tính diện tích của miếng pizza trong Hình 4a theo góc ở tâm và bán kính của ổ bánh hay không?
b) Chia một hình tròn bán kính R thành 360 phần bằng nhau.
i) Tính diện tích mỗi phần đó.
ii) Tính diện tích phần hình tròn ghép bởi n phần bằng nhau nó trên (Hình 4b).
Bài 14 :
Tính diện tích hình quạt tròn với bán kính R = 20 cm, ứng với cung 72o.
Bài 15 :
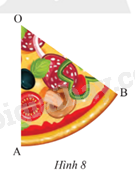
Tính diện tích của miếng bánh pizza có dạng hình quạt tròn trong Hình 8. Biết OA = 15 cm và \(\widehat {AOB} = {55^o}\).
Bài 16 :
Tính diện tích hình quạt tròn ứng với cung số đo lần lượt là \({30^o};{90^o};{120^o}\) của hình tròn (O; 12 cm)
Bài 17 :
Tính diện tích hình quạt tròn ứng với cung có độ dài lần lượt là 8 cm, 15 cm của hình tròn (O; 5 cm)
Bài 18 :
Hình quạt tròn bán kính R, ứng với cung 90o có diện tích bằng
A. \(\pi {R^2}\)
B. \(\frac{{\pi {R^2}}}{2}\)
C. \(\frac{{\pi {R^2}}}{4}\)
D. \(\frac{{\pi {R^2}}}{8}\)
Bài 19 :
Vẽ đường tròn \(\left( {O;2cm} \right)\) và các điểm \(A,B\) thỏa mãn \(OA < 2cm,OB = 2cm\). Nêu nhận xét về vị trí của các điểm \(A,B\) so với đường tròn \(\left( {O;2cm} \right)\).
Bài 20 :
Quan sát Hình 71, hãy cho biết phần hình tròn \(\left( O \right)\) tô màu xanh được giới hạn bởi hai bán kính và cung nào?
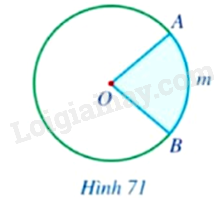
Bài 21 :
Cho hình quạt tròn \(COD\) giới hạn bởi hai bán kính \(OC,OD\) và cung \(CnD\) sao cho \(OC = OD\) (Hình 74). Hãy tìm số đo cung \(CqD\) ứng với hình quạt đó.
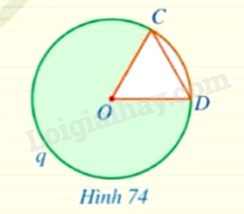
Bài 22 :
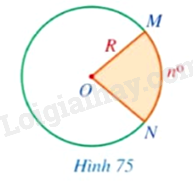
Ta coi mỗi hình tròn bán kính \(R\) là một hình quạt có số đo \(360^\circ \). Tính diện tích hình quạt tròn tâm \(O\), bán kính \(R\), biết số đo cung ứng với hình quạt tròn đó là:
a) \(1^\circ \)
b) \(n^\circ \) (Hình 75).
Bài 23 :
Hình quạt tô màu đỏ ở Hình 65 có bán kính bằng 2 dm và góc ở tâm bằng \(150^\circ \).
a) Tính diện tích của hình quạt đó theo đơn vị decimét vuông (làm tròn kết quả đến hàng phần trăm).
b) Tính chiều dài cung tương ứng với hình quạt tròn đó.

Bài 24 :
Logo ở Hình 95 có dạng một hình quạt tròn bán kính 8cm và góc ở tâm bằng \(60^\circ \). Tính diện tích mỗi hình sau (theo đơn vị centimét vuông và làm tròn kết quả đến hàng phần mười):
a) Toàn bộ logo;
b) Phần logo màu đỏ có dạng hình viên phân.

Bài 25 :
Hình 96 biểu diễn vùng biển được chiếu sáng bởi một hải đăng có dạng một hình quạt tròn với bán kính 18 dặm, cung \(AmB\) có số đo \(245^\circ \).
a) Hãy tính diện tích vùng biển có thể nhìn thấy ánh sáng từ hải đăng theo đơn vị kilomét vuông (lấy 1 dặm = 1609m, \(\pi = 3,14\) và làm tròn kết quả đến hàng đơn vị).
b) Giả sử một con thuyền di chuyển dọc theo dây cung có độ dài 28 dặm của đường tròn với tâm là tâm của hình quạt tròn, bán kính 18 dặm. Tính khoảng cách nhỏ nhất từ con thuyền đến hải đăng (theo đơn vị dặm và làm tròn kết quả đến hàng đơn vị).

Bài 26 :
Tính diện tích của hình quạt tròn bán kính 3cm ứng với cung \({210^o}\).
Bài 27 :
Trong Hình 5.74, độ dài cạnh của các hình vuông lớn là 10cm. Tính diện tích và chu vi của phần được tô màu.
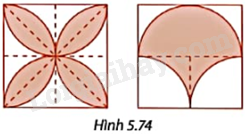
Bài 28 :
Hình quạt tròn bán kính R(cm) ứng với cung \({240^o}\) có diện tích bằng \(6\pi \;c{m^2}\). Bán kính R bằng
A. 3cm.
B. 6cm.
C. 9cm.
D. 12cm.
Bài 29 :
Tại một vòng xoay ngã tư, người ta cần làm các bồn trồng hoa như hình 1. Em hãy tính phần diện tích của 1 bồn hoa ở hình 2 (phần được tô đậm). Biết rằng bán kính của vòng tròn lớn là 7m, vòng tròn nhỏ là 3m, số đo cung tròn đó là \(60^\circ \). (làm tròn đến hàng phần mười)

-
A.
\(20,9{m^2}\).
-
B.
\(41,9{m^2}\).
-
C.
\(2,1{m^2}\).
-
D.
\(10,5{m^2}\).
Bài 30 :
Máy kéo nông nghiệp có hai bánh sau to hơn hai bánh trước. Khi bơm căng, bánh xe sau có đường kính là 1,672m và bánh xe trước có đường kính là 88cm. Hỏi khi bánh xe sau lăn được 10 vòng thì bánh xe trước lăn được mấy vòng?

-
A.
\(\frac{{19}}{2}\).
-
B.
\(19\).
-
C.
\(38\).
-
D.
\(20\).


















Danh sách bình luận