Cho tam giác ABC vuông tại A có đường cao AH. Hình chiếu của H trên AB, AC lần lượt là D, E. Gọi (O) là đường tròn đường kính HB và (O') là đường tròn đường kính HC. Chứng minh:
a) Điểm D thuộc đường tròn (O) và điểm E thuộc đường tròn (O’);
b) Hai đường tròn (O) và (O') tiếp xúc ngoài;
c) AH là tiếp tuyến chung của hai đường tròn (O) và (O’);
d) AH = DE;
e) Diện tích tứ giác DEO’O bằng nửa diện tích tam giác ABC.
a) Chứng minh \(OB = OD = OH = \frac{{BH}}{2}\); \(O'H = O'E = O'C = \frac{{HC}}{2}\).
b) Chứng minh \(OO' = OH + O'H\).
c) Chứng minh \(AH \bot OO'\).
d) Chứng minh ADHE là hình chữ nhật.
e) Bước 1: Chứng minh ODEO’ là hình thang vuông.
Bước 2: Biểu diễn diện tích 2 hình theo công thức.
Bước 3: Vận dụng dữ kiện \(AH = DE\), \(BC = BH + CH = 2\left( {OD + O'E} \right)\) để biến đổi.
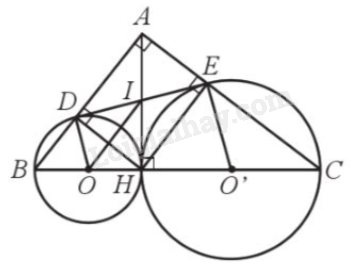
a) Do tam giác BDH vuông tại D và O là trung điểm của BH (BO và HO là bán kính đường tròn (O)) nên \(OB = OD = OH = \frac{{BH}}{2}\), do đó D thuộc đường tròn (O).
Do tam giác ECH vuông tại E và O’ là trung điểm của CH (O’H và O’C là bán kính đường tròn (O)) nên \(O'H = O'E = O'C = \frac{{HC}}{2}\), do đó E thuộc đường tròn (O’).
b) Do tam giác ABC vuông tại A có AH là đường cao, \(H \in BC\) nên H nằm giữa B và C.
Mà (O) là đường tròn đường kính HB và (O') là đường tròn đường kính HC nên H nằm giữa O và O’, do đó \(OO' = OH + O'H\), vậy đường tròn (O) và (O') tiếp xúc ngoài.
c) Ta có OH, O’H lần lượt là bán kính của (O) và (O’) , và AH vuông góc với OO’ tại H nên AH là tiếp tuyến chung của hai đường tròn (O) và (O’).
d) Do tam giác BDH vuông tại D nên \(\widehat {BDH} = 90^\circ \), do đó \(\widehat {HDA} = 90^\circ \).
Do tam giác ECH vuông tại E nên \(\widehat {ECH} = 90^\circ \), do đó \(\widehat {HEA} = 90^\circ \).
Xét tứ giác ADHE có \(\widehat {HDA} = \widehat {HEA} = \widehat {DAE} = 90^\circ \) nên ADHE là hình chữ nhật, do đó \(AH = DE\).
e) Do ADHE là hình chữ nhật nên \(IA = ID = IH = IE\).
Xét hai tam giác OID và OIH có:
\(OD = OH\);
OI chung;
\(ID = IH\)
Suy ra \(\Delta OID = \Delta OIH\) (c.c.c), do đó \(\widehat {OHI} = \widehat {ODI} = 90^\circ \), hay \(OD \bot DE\).
Xét hai tam giác OIE và O’IH có:
\(O'E = O'H\);
O’I chung;
\(IE = IH\)
Suy ra \(\Delta OIE = \Delta O'IH\)(c.c.c), do đó \(\widehat {O'HI} = \widehat {O'EI} = 90^\circ \), hay \(O'E \bot DE\).
Xét ODEO’ có \(OD \bot DE\), \(O'E \bot DE\) nên \(OD//EO'\), do đó ODEO’ là hình thang vuông và DE là đường cao.
Diện tích hình thang ODEO’ và tam giác ABC lần lượt là: \({S_1} = \frac{{DE\left( {OD + O'E} \right)}}{2};{S_2} = \frac{{AH.BC}}{2}\)
Mà \(AH = DE\), \(BC = BH + CH = 2\left( {OD + O'E} \right)\)
Suy ra \({S_1} = \frac{1}{2}{S_2}\).
Vậy diện tích tứ giác DEO’O bằng nửa diện tích tam giác ABC.

Các bài tập cùng chuyên đề
Bài 1 :
Cho $\left( {O;R} \right)$. Đường thẳng $d$ là tiếp tuyến của đường tròn $\left( {O;R} \right)$ tại tiếp điểm $A$ khi
-
A.
$d \bot OA$ tại $A$ và $A \in \left( O \right)$
-
B.
$d \bot OA$
-
C.
$A \in \left( O \right)$
-
D.
$d{\rm{//}}OA$
Bài 2 :
Cho $\left( {O;5cm} \right)$. Đường thẳng $d$ là tiếp tuyến của đường tròn $\left( {O;5\,cm} \right)$, khi đó
-
A.
Khoảng cách từ $O$ đến đường thẳng $d$ nhỏ hơn $5\,cm$
-
B.
Khoảng cách từ $O$ đến đường thẳng $d$ lớn hơn $5\,cm$
-
C.
Khoảng cách từ $O$ đến đường thẳng $d$ bằng $5\,cm$
-
D.
Khoảng cách từ $O$ đến đường thẳng $d$ bằng $6\,cm$
Bài 3 :
Cho tam giác $ABC$ có $AC = 3cm,AB = 4cm,BC = 5cm$. Vẽ đường tròn $\left( {C;CA} \right)$. Khẳng định nào sau đây là đúng?
-
A.
Đường thẳng $BC$ cắt đường tròn $\left( {C;CA} \right)$ tại một điểm
-
B.
$AB$ là cát tuyến của đường tròn $\left( {C;CA} \right)$
-
C.
$AB$ là tiếp tuyến của $\left( {C;CA} \right)$
-
D.
$BC$ là tiếp tuyến của $\left( {C;CA} \right)$
Bài 4 :
Cho tam giác $ABC$ cân tại $A$; đường cao $AH$ và $BK$ cắt nhau tại $I$. Khi đó đường thẳng nào sau đây là tiếp tuyến của đường tròn đường kính $AI$.
-
A.
$HK$
-
B.
$IB$
-
C.
$IC$
-
D.
$AC$
Bài 5 :
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$. Đường tròn đường kính $BH$ cắt $AB$ tại $D$, đường tròn đường kính $CH$ cắt $AC$ tại $E$ . Chọn khẳng định sai trong các khẳng định sau
-
A.
$DE$ là cắt đường tròn đường kính $BH$
-
B.
$DE$ là tiếp tuyến của đường tròn đường kính $BH$
-
C.
Tứ giác$AEHD$ là hình chữ nhật
-
D.
$DE \bot DI$ (với $I$ là trung điểm $BH$)
Bài 6 :
Cho đường tròn $(O;R)$ đường kính $AB$. Vẽ dây $AC$ sao cho \(\widehat {ABC} = 30^\circ \) . Trên tia đối của tia $AB$ lấy điểm $M$ sao cho $AM = R$ .
Bài 7 :
Từ một điểm $A$ ở bên ngoài đường tròn $\left( {O;R} \right)$,vẽ hai tiếp tuyến $AB,AC$ với $\left( O \right)$. Đường thẳng vuông góc với $OB$ tại $O$ cắt tia $AC$ tại $N$. Đường thẳng vuông góc với $OC$ tại $O$ cắt tia $AB$ tại $M$.
Bài 8 :
Cho đường tròn$\left( O \right)$ , dây $AB$ khác đường kính. Qua $O$ kẻ đường vuông góc với $AB$ , cắt tiếp tuyến tại $A$ của đường tròn ở điểm $C$ .
Bài 9 :
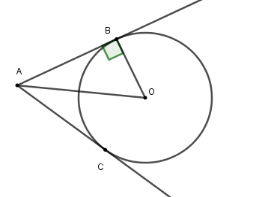
Cho hình vẽ dưới đây. Biết \(\widehat {BAC} = {60^0};AO = 10\,cm\). Chọn đáp án đúng.
Bài 10 :
Nếu đường thẳng $d$ là tiếp tuyến của đường tròn $\left( O \right)$ tại $A$ thì
-
A.
$d{\rm{//}}OA$
-
B.
$d \equiv OA$
-
C.
$d \bot OA$ tại$A$
-
D.
$d \bot OA$ tại $O$
Bài 11 :
Cho đường tròn tâm $O$ bán kính $3cm$ và một điểm $A$ cách $O$ là $5cm$. Kẻ tiếp tuyến $AB$ với đường tròn ( $B$ là tiếp điểm). Tính độ dài $AB$.
-
A.
$AB = \,3\,cm$
-
B.
$AB = \,4\,cm$
-
C.
$AB = \,5\,cm$
-
D.
$AB = \,2\,cm$
Bài 12 :
Cho đường tròn $\left( {O;R} \right)$ và dây $AB = 1,2R$. Vẽ một tiếp tuyến song song với $AB$, cắt các tia $OA,OB$ lần lượt tại $E$ và $F$. Tính diện tích tam giác $OEF$ theo $R$.
-
A.
${S_{OEF}} = 0,75{R^2}$
-
B.
${S_{OEF}} = 1,5{R^2}$
-
C.
${S_{OEF}} = 0,8{R^2}$
-
D.
${S_{OEF}} = 1,75{R^2}$
Bài 13 :
Cho đường tròn $\left( O \right)$, bán kính $OA$. Dây $CD$ là đường trung trực của $OA$.
Bài 14 :
Cho tam giác $ABC$ có $AB = 5,AC = 12,BC = 13$. Khi đó:
-
A.
$AB$ là tiếp tuyến của đường tròn $\left( {C;5} \right)$
-
B.
$AC$ là tiếp tuyến của đường tròn $\left( {B;5} \right)$
-
C.
$AB$ là tiếp tuyến của đường tròn $\left( {B;12} \right)$
-
D.
$AC$ là tiếp tuyến của đường tròn $\left( {C;13} \right)$
Bài 15 :
“Nếu một đường thẳng đi qua một điểm của đường tròn và … thì đường thẳng ấy là một tiếp tuyến của đường tròn”. Cụm từ thích hợp điền vào chỗ trống là
-
A.
song song với bán kính đi qua điểm đó
-
B.
vuông góc với bán kính đi qua điểm đó
-
C.
song song với bán kính đường tròn
-
D.
vuông góc với bán kính bất kì
Bài 16 :
Cho \(\left( {O;4cm} \right)\). Đường thẳng \(d\) là tiếp tuyến của đường tròn \(\left( {O;4\,cm} \right)\), khi đó
-
A.
Khoảng cách từ \(O\) đến đường thẳng \(d\) nhỏ hơn \(4\,cm\)
-
B.
Khoảng cách từ \(O\) đến đường thẳng \(d\) bằng \(4\,cm\)
-
C.
Khoảng cách từ \(O\) đến đường thẳng \(d\) lớn hơn \(4\,cm\)
-
D.
Khoảng cách từ \(O\) đến đường thẳng \(d\) bằng \(5\,cm\)
Bài 17 :
Cho tam giác \(MNP\) có \(MN = 5cm,NP = 12cm,MP = 13cm\). Vẽ đường tròn \(\left( {M;NM} \right)\). Khẳng định nào sau đây là đúng?
-
A.
\(NP\) là tiếp tuyến của \(\left( {M;MN} \right)\)
-
B.
\(MP\) là tiếp tuyến của \(\left( {M;MN} \right)\)
-
C.
\(\Delta MNP\) vuông tại \(M\)
-
D.
\(\Delta MNP\) vuông tại \(P\)
Bài 18 :
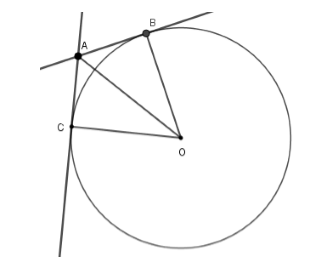
Cho hình vẽ dưới đây. Biết \(AB\) và \(AC\) là hai tiếp tuyến của \(\left( O \right),\) \(\widehat {BAC} = {120^0};AO = 8\,cm\). Chọn đáp án đúng.
Bài 19 :
Cho hình chữ nhật ABCD, H là hình chiếu của A lên BD. M, N lần lượt là trung điểm của BH, CD. Đường nào sau đây là tiếp tuyến của đường tròn tâm A, bán kính AM.
-
A.
\(BN\)
-
B.
\(MN\)
-
C.
\(AB\)
-
D.
\(CD\)
Bài 20 :
Cho đường tròn \(\left( O \right)\) , dây \(MN\) khác đường kính. Qua \(O\) kẻ đường vuông góc với \(MN\) , cắt tiếp tuyến tại \(M\) của đường tròn ở điểm \(P\) .
Bài 21 :
Cho đường tròn \((O;2cm)\) bán kính \(OB.\) Vẽ dây \(BC\) sao cho \(\widehat {OBC} = 60^\circ .\) Trên tia \(OB\) lấy điểm \(M\) sao cho \(BM = 2cm.\)
Bài 22 :
Cho nửa đường tròn (O ; R), AB là đường kính. Dây BC có độ dài R. Trên tia đối của tia CB lấy điểm D sao cho \(CD = 3R. \) Chọn câu đúng.
-
A.
AD là tiếp tuyến của đường tròn.
-
B.
\(\widehat {ACB} = 90^\circ \)
-
C.
\(AD\) cắt đường tròn \(\left( {O;R} \right)\) tại hai điểm phân biệt
-
D.
Cả A, B đều đúng.
Bài 23 :
Cho đường tròn \(\left( O \right)\) và điểm \(A\) nằm trên đường tròn \(\left( O \right).\) Nếu đường thẳng \(d \bot OA\) tại \(A\) thì
-
A.
\(d\) là tiếp tuyến của \(\left( O \right)\)
-
B.
\(d\) cắt \(\left( O \right)\) tại hai điểm phân biệt
-
C.
\(d\) là tiếp xúc với \(\left( O \right)\) tại \(O\)
-
D.
Cả A, B, C đều sai
Bài 24 :
Cho đường tròn tâm \(O\) bán kính \(6cm\) và một điểm \(A\) cách \(O\) là \(10cm\). Kẻ tiếp tuyến \(AB\) với đường tròn ( \(B\) là tiếp điểm). Tính độ dài \(AB\).
-
A.
\(AB = \,12\,cm\)
-
B.
\(AB = \,4\,cm\)
-
C.
\(AB = \,6\,cm\)
-
D.
\(AB = \,8\,cm\)
Bài 25 :
Cho đường tròn \(\left( {O;6cm} \right)\) và dây \(AB = 9,6cm\). Vẽ một tiếp tuyến song song với \(AB\), cắt các tia \(OA,OB\) lần lượt tại \(E\) và \(F\). Tính diện tích tam giác \(OEF\) theo \(R\).
-
A.
\({S_{OEF}} = 36\,\left( {c{m^2}} \right)\)
-
B.
\({S_{OEF}} = 24\,\left( {c{m^2}} \right)\)
-
C.
\({S_{OEF}} = 48\,\left( {c{m^2}} \right)\)
-
D.
\({S_{OEF}} = 96\,\left( {c{m^2}} \right)\)
Bài 26 :
Cho đoạn thẳng OH và đường thẳng a vuông góc với OH tại H.
a) Xác định khoảng cách từ O đến đường thẳng a.
b) Nếu vẽ đường tròn (O; OH) thì đường tròn này và đường thẳng a có vị trí tương đối như thế nào?
Bài 27 :
Cho một hình vuông có độ dài mỗi cạnh bằng 6 cm và hai đường chéo cắt nhau tại I. Chứng minh rằng đường tròn (I; 3cm) tiếp xúc với cả bốn cạnh của hình vuông.
Bài 28 :
Cho đường thẳng a và điểm M không thuộc a. Hãy vẽ đường tròn tâm M tiếp xúc với a.
Bài 29 :
Trở lại tình huống mở đầu. Ở đây, ta hiểu đồng xu nằm đè lên một đường thẳng khi đường tròn (hình ảnh của đồng xu) và đường thẳng ấy cắt nhau.
Bằng cách xét vị trí của tâm đồng xu trong một dải nằm giữa hai đường thẳng song song cạnh nhau (cách đều hoặc không cách đều hai đường thẳng đó), hãy chứng minh rằng chỉ xảy ra các trường hợp a và b, không thể xảy ra trường hợp c.

Bài 30 :
Cho điểm M ở bên ngoài một đường tròn tâm O. Hãy dùng thước và compa thực hiện các bước vẽ hình như sau:
- Vẽ đường tròn đường kính MO cắt đường tròn (O) tại A và B;
- Vẽ và chứng tỏ các đường thẳng MA và MB là hai tiếp tuyến của (O).


















Danh sách bình luận