Cho bảng gồm 2 015 x 2015 ô vuông nhỏ (Hình 9).
Điền vào mỗi ô của hàng số 1 hoặc số -1.
Bên trái mỗi dòng thứ i ghi tích các số của dòng đó và đặt là xi . Dưới mỗi cột thứ j ghi tích các số của cột đó và đặt là yj .
(i = 1;2;3;…2 015 và j = 1;2;3;…; 2 015)
Chứng tỏ rằng tổng của 4030 số xi; yj nhận được khác 0
Ta giả sử tổng của 4030 số xi; yj nhận được = 0. Ta sẽ đi chứng minh điều giả sử này là sai
Giả sử tổng của 4030 số xi; yj nhận được = 0
Ta có: x1 + x2 +…+ x2015 + y1 + y2 +…+y2015 =0; xi, yj đều bằng 1 hoặc -1. Do vậy, số vị trí nhận giá trị 1 bằng số vị trí nhận giá trị -1. Ta được, trong 4030 số xi; yj thì có 2015 số bằng 1 và 2015 số bằng -1.
Tích x1x2….x2015.y1.y2…y2015 = -1 (*)
Mà x1x2….x2015 = y1.y2…y2015 (đều là tích các số trong bảng) nên x1x2….x2015.y1.y2…y2015 = (x1x2….x2015)2 =1 (mâu thuẫn với (*))
Vậy tổng của 4030 số xi; yj là khác 0

Các bài tập cùng chuyên đề
Bài 1 :
Tính nhanh $\left( { - 5} \right).125.\left( { - 8} \right).20.\left( { - 2} \right)$ ta được kết quả là
-
A.
\( - 200000\)
-
B.
\( - 2000000\)
-
C.
\(200000\)
-
D.
\( - 100000\)
Bài 2 :
Tính hợp lý \(A = - 43.18 - 82.43 - 43.100\)
-
A.
\(0\)
-
B.
\( - 86000\)
-
C.
\( - 8600\)
-
D.
\( - 4300\)
Bài 3 :
Tính nhanh \({( - 4)^2}{.3^2}.{\left( { - 5} \right)^3}\) ta được kết quả là:
-
A.
\( - 18000\)
-
B.
\(18000\)
-
C.
\( - 20000\)
-
D.
\(20000\)
Bài 4 :
Tính hợp lý \(B = - 55.78 + 13.\left( { - 78} \right) - 78.\left( { - 65} \right)\).
-
A.
\(1\)
-
B.
\(234\)
-
C.
\( - 234\)
-
D.
\(130\)
Bài 5 :
Tính hợp lí: \(( - 3).29 + \left( { - 3} \right).( - 99) + ( - 3).( - 30) = ?\)
-
A.
\(300\)
-
B.
\( - 120\)
-
C.
\(120\)
-
D.
\( - 300\)
Bài 6 :
Tính hợp lí: \(( - 3).54 + \left( { - 3} \right).( - 14) + ( - 3).60 = ?\)
-
A.
\(300\)
-
B.
\( - 120\)
-
C.
\(120\)
-
D.
\( - 300\)
Bài 7 :
Tính một cách hợp lí:
a) 4. (1 930 + 2019) + 4.(-2019);
b) (-3).(-17) + 3. (120 - 17).
Bài 8 :
Tính giá trị của biểu thức sau một cách hợp lí:
a) (-8). 72 +8. (-19) - (-8);
b) (-27).1011 - 27.(-12) + 27.(-1).
Bài 9 :
a) 15.(-236) + 15.235;
b) 237. (-28) + 28. 137;
c) 38. (27 - 44) - 27.(38 - 44).
Bài 10 :
Tính giá trị của biểu thức P = (-35). x - (-15) - 37 trong mỗi trường hợp sau:
a) x = 15; b) x = -37.
Bài 11 :
Tính một cách hợp lí:
a) 17.[29 - (-111)] + 29.(-17);
b) 19.43 + (-20).43 - (-40).
Bài 12 :
Tính a(b + c) và ab + ac khi a = -2, b = 14, c = -4.
Bài 13 :
1. a) Tính giá trị của tích P = 3. (-4) . 5. (-6);
b) Tích P sẽ thay đổi thế nào nếu ta đối dấu tất cả các thừa số?
2. Tính 4. (-39) - 4 .(-14).
Bài 14 :
Thực hiện các phép tính rồi so sánh kết quả tương ứng ở hai cột màu xanh và màu đỏ.
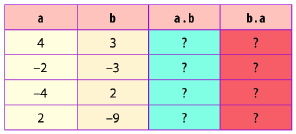
Bài 15 :
Thực hiện các phép tính rồi so sánh kết quả tương ứng ở hai cột màu xanh và màu đỏ.
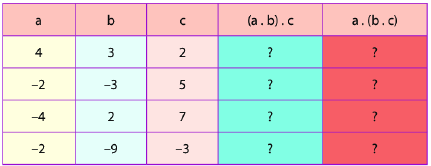
Bài 16 :
a) P là tích của 8 số nguyên khác 0 trong đó có đúng 4 số dương. Q là tích của 6 số nguyên khác 0 trong đó có duy nhất một số dương. Hãy cho biết P và Q là số dương hay số âm.
b) Tích của một số lẻ các số nguyên âm có dấu gì?
c) Tích của một số chẵn các số nguyên âm có dấu gì?
Bài 17 :
Thực hiện các phép tính rồi so sánh kết quả tương ứng ở hai cột màu xanh và màu đỏ.
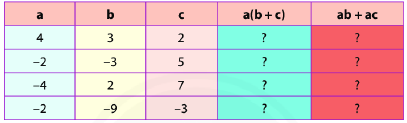
Bài 18 :
Thực hiện phép tính: \(\left( { - 2} \right).29 + \left( { - 2} \right).\left( { - 99} \right)\)\( + \left( { - 2} \right).\left( { - 30} \right)\)
Bài 19 :
Tính một cách hợp lí:
a) (- 16) . (- 7) . 5;
b) 11 . (- 12) + 11 . (- 18);
c) 87 . (- 19) – 37 . (- 19);
d) 41 . 81 . (- 451) . 0
Bài 20 :
Chọn từ “âm”, “dương” thích hợp cho “?”
a) Tích ba số nguyên âm là một số nguyên “?”
b) Tích hai số nguyên âm với một số nguyên dương là một số nguyên “?”
c) Tích của một số chẵn các số nguyên âm là một số nguyên “?”
d) Tích của một số lẻ các số nguyên âm là một số nguyên “?”
Bài 21 :
Tính và so sánh kết quả:
a) (- 4) . 7 và 7 . (- 4);
b) [(- 3) . 4] . (- 5) và (- 3) . [4 . (- 5)];
c) (- 4) . 1 và - 4;
d) (- 4) . (7 + 3) và (- 4) . 7 + 7 . (- 4) . 3.
Bài 22 :
Tính một cách hợp lí:
a) (- 6) . (- 3) . (- 5)
b) 41 . 81 – 41 . (- 19).
Bài 23 :
Tìm số nguyên x, biết:
a) 9. (x + 28) = 0;
b) (27 – x). (x + 9) = 0;
c) (-x). (x – 43) = 0.
Bài 24 :
Tính một cách hợp lí:
a) (29 – 9). (-9) + (-13 – 7). 21;
b) (-157). (127 – 316) – 127. (316 – 157).
Bài 25 :
Tính giá trị của biểu thức; tìm cách tính hợp lí:
a) 21. 23 – 3. 7. (-17);
b) 42. 3 – 7. [(-34) + 18].
Bài 26 :
Tính giá trị của biểu thức; tìm cách tính hợp lí:
a) 71. 64 + 32. (-7) – 13. 32;
b) 13. (23 – 17) – 13. (23 + 17).
Bài 27 :
Tính theo hai cách:
a) 18 . 15 – 3. 6 . 10;
b) 63 – 9 . (12 + 7);
c) 39 . (29 -13) – 29 . (39 - 13).
Bài 28 :
Chọn số thích hợp cho [?]
Bài 29 :
Tính một cách hợp lí:
a) (-16) . (-9) . 5
b) (-15) . 999
c) (-25) . 144 . (-4)
d) (-125) . 2 020 . (-8)
e) (- 2 021) . (-15) + (-15) . 2 020
g) 121 . (-63) + 63 . (-53) – 63 . 26
Bài 30 :
So sánh hai biểu thức sau mà không tính cụ thể giá trị của chúng:
a) (-2 021) . 2 021 và (- 2 020) . 2 022
b) (8 765 – 5 678) . [ 5 678 – 9 765 + (-12)] và 4 342.


















Danh sách bình luận