Cho dãy số \(({u_n})\) được xác định bởi \(\left\{ {\begin{array}{*{20}{c}}{{u_1} = 3}\\{{u_{n + 1}} = 2{u_n}}\end{array}} \right.\) với \(n \ge 1\). Khi đó
a) Dãy số \(({u_n})\) là dãy số giảm
b) Dãy số \(({u_n})\) là dãy số bị chặn
c) \({u_2} = 6\)
d) Công thức tổng quát của \(({u_n})\) là \({u_n} = {2^{n - 1}}.3\)
a) Dãy số \(({u_n})\) là dãy số giảm
b) Dãy số \(({u_n})\) là dãy số bị chặn
c) \({u_2} = 6\)
d) Công thức tổng quát của \(({u_n})\) là \({u_n} = {2^{n - 1}}.3\)
a) Dãy số \(({u_n})\) là dãy số giảm nếu \({u_n} > {u_{n + 1}}\). Dãy số \(({u_n})\) là dãy số tăng nếu \({u_n} < {u_{n + 1}}\).
b) Dãy số \(({u_n})\) là dãy số bị chặn nếu \(({u_n})\) vừa bị chặn trên vừa bị chặn dưới, tức tồn tại hai số m, M sao cho \(m \le {u_n} \le M\) \(\forall n \in \mathbb{N}*\).
c) Tính \({u_2}\) bằng công thức \({u_{n + 1}} = 2{u_n}\).
d) Tìm số hạng đầu \({u_1}\) và công sai d. Công thức tổng quát: \({u_n} = {u_1}.{q^{n - 1}}\).
a) Sai. Ta có: \({u_1} = 3 > 0\). Với n = 1, ta được \({u_2} = 2{u_1} = 2.3 = 6 > 0\).
Giả sử n = k, ta cần chứng minh \({u_k} > 0\) thì \({u_{k + 1}} > 0\).
Thật vậy, \({u_{k + 1}} = 2{u_k} > 0\) vì \({u_k} > 0\).
Vậy \({u_n} > 0\) \(\forall n \ge 1\).
Ta có: \({u_{n + 1}} - {u_n} = 2{u_n} - {u_n} = {u_n} > 0\). Suy ra \({u_n} < {u_{n + 1}}\). Vậy dãy số trên là dãy số tăng.
b) Sai. Ta có: \(({u_n})\) là dãy số tăng nên \(({u_n})\) bị chặn dưới tại \({u_1} = 3\).
Mặt khác, \(({u_n})\) là cấp số nhân có công bội \(q = \frac{{{u_{n + 1}}}}{{{u_n}}} = \frac{{2{u_n}}}{{{u_n}}} = 2\) và số hạng đầu \({u_1} = 3\) nên công thức tổng quát là \({u_n} = {3.2^{n - 1}}\). Ta có \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = \mathop {\lim }\limits_{n \to + \infty } {3.2^{n - 1}} = + \infty \) nên dãy không bị chặn trên.
Vậy dãy số không bị chặn.
c) Đúng. \({u_2} = 2{u_1} = 2.3 = 6\).
d) Đúng. Theo câu b), công thức tổng quát là \({u_n} = {3.2^{n - 1}}\).

Các bài tập cùng chuyên đề
Bài 1 :
Chị Mai gửi tiền tiết kiệm vào ngân hàng theo thể thức lãi kép như sau: Lần đầu chị gửi 100 triệu đồng. Sau đó, cứ hết 1 tháng chị lại gửi thêm vào ngân hàng 6 triệu đồng. Biết lãi suất của ngân hàng là 0,5% một tháng. Gọi \({P_n}\) (triệu đồng) là số tiền chị có trong ngân hàng sau n tháng
a) Tính số tiền chị có trong ngân hàng sau 1 tháng
b) Tính số tiền chị có trong ngân hàng sau 3 tháng
c) Dự đoán công thức của \({P_n}\) tính theo n
Bài 2 :
Trên lưới ô vuông, mỗi ô cạnh 1 đơn vị, người ta vẽ 8 hình vuông và tô màu khác nhau như Hình 3. Tìm dãy số biểu diễn độ dài cạnh của 8 hình vuông đỏ từ nhỏ đến lớn. Có nhận xét gì về dãy số trên?
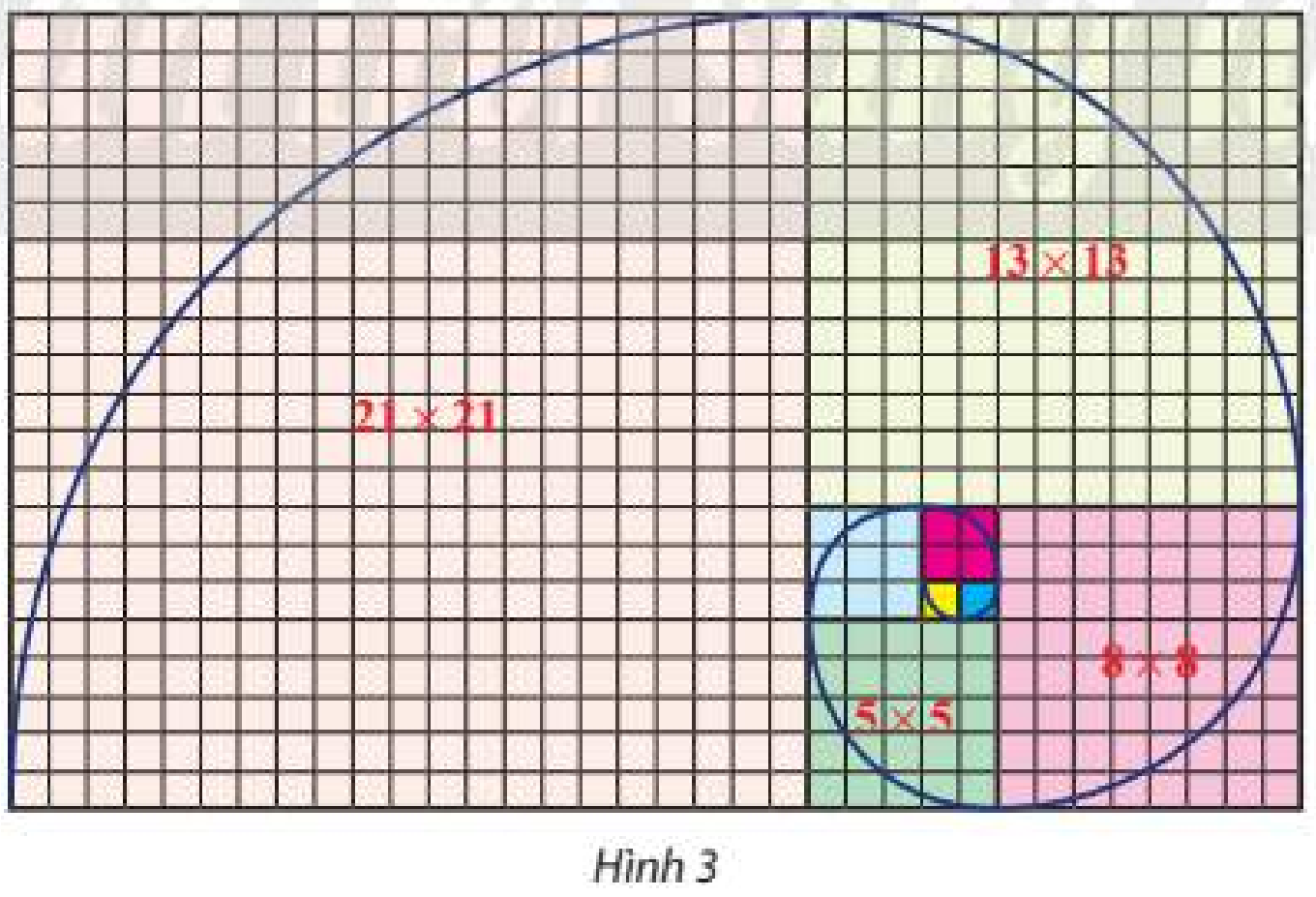
Bài 3 :
Số hạng thứ 4 của dãy số \(\left\{ {\begin{array}{*{20}{c}}{{u_1} = 1}\\{{u_n} = \frac{1}{{{u_{n - 1}} + 2}}}\end{array}} \right.\) là?
-
A.
\(\frac{7}{{17}}\)
-
B.
\(\frac{7}{{15}}\)
-
C.
\(\frac{8}{7}\)
-
D.
\(\frac{3}{8}\)
Bài 4 :
Số hạng thứ 3 của dãy số \(\left\{ {\begin{array}{*{20}{c}}{{u_1} = 1}\\{{u_n} = 2{u_{n - 1}} + 3}\end{array}} \right.\) là?
-
A.
5
-
B.
8
-
C.
28
-
D.
13
Bài 5 :
Cho dãy số \(({u_n})\) biết \({u_n} = {2^n} + 1\). Khi đó
a) Dãy số \(({u_n})\) là dãy số tăng
b) Dãy số \(({u_n})\) là dãy số bị chặn
c) \({u_6} = 65\)
d) Số hạng thứ n + 2 của dãy số là \({u_{n + 2}} = {2^n}.2\)
Bài 6 :
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = {2^n}.\) Số hạng \({u_{n + 1}}\) là
-
A.
\({u_{n + 1}} = {2^n}.2\)
-
B.
\({u_{n + 1}} = {2^n} + 1\)
-
C.
\({u_{n + 1}} = 2\left( {n + 1} \right)\)
-
D.
\({u_{n + 1}} = {2^n} + 2\)
Bài 7 :
Cho dãy số \(({u_n})\) biết \({u_n} = {2^n}\). Khi đó
a) Dãy số \(({u_n})\) là dãy số tăng
b) Dãy số \(({u_n})\) là dãy số bị chặn
c) \({u_8} = 64\)
d) Số hạng thứ n + 2 của dãy số là \({u_{n + 2}} = {2^n}.2\)
Bài 8 :
Cho dãy số \(({u_n})\) được xác định bởi \({u_n} = \frac{{{n^2} + 3n + 7}}{{n + 1}}\). Dãy số có bao nhiêu số hạng nhận giá trị nguyên?
Bài 9 :
Tìm số hạng thứ tám của một cấp số cộng là 75 và số hạng thứ hai mươi là 39.
a) Tìm số hạng đầu và công sai của cấp số cộng
b) Tìm hệ thức truy hồi cho cấp số cộng.
c) Tìm công thức số hạng thứ n của cấp số cộng.
Bài 10 :
Để tính xấp xỉ giá trị \(\sqrt p ,\) người ta có thể dùng dãy số cho bởi hệ thức truy hồi sau: \({u_1} = k,{u_n} = \frac{1}{2}\left( {{u_{n - 1}} + \frac{p}{{{u_{n - 1}}}}} \right)\) với \(n \ge 2\), ở đó k là một giá trị dự đoán ban đầu của \(\sqrt p .\)
Sử dụng hệ thức truy hồi này, hãy tính xấp xỉ các giá trị sau bằng cách tính \({u_5}\) và tính sai số tuyệt đối khi so với giá trị bằng máy tính cầm tay (làm tròn kết quả đến chữ số thập phân thứ năm)
a) \(\sqrt 5 \) (lấy \(k = 3\));
b) \(\sqrt 8 \) (lấy \(k = 3\));
Bài 11 :
Cho dãy số \(\left( {{u_n}} \right)\) xác định bởi hệ thức truy hồi: \({u_1} = 1,{u_{n + 1}} = {u_n} + \left( {n + 1} \right)\)
a) Mỗi số hạng của dãy số này gọi là một số tam giác. Viết bảy số tam giác đầu.
b) Biết rằng \(1 + 2 + ... + n = \frac{{n\left( {n + 1} \right)}}{2}\). Hãy chứng tỏ công thức của số hạng tổng quát là: \({u_{n + 1}} = \frac{{\left( {n + 1} \right)\left( {n + 2} \right)}}{2}\).
c) Chứng minh rằng \({u_{n + 1}} + {u_n} = {\left( {n + 1} \right)^2}\), tức là tổng của hai số tam giác liên tiếp là một số chính phương.
Bài 12 :
Một công ty dược phẩm đang thử nghiệm một loại thuốc mới. Một thí nghiệm bắt đầu với \(1,0 \times {10^9}\) vi khuẩn. Một liều thuốc được sử dụng sau mỗi bốn giờ có thể tiêu diệt được \(4,0 \times {10^8}\) vi khuẩn. Giữa các liều thuốc, số lượng vi khuẩn có thể tăng lên 25%.
a) Viết hệ thức truy hồi cho số lượng vi khuẩn sống trước mỗi lần sử dụng.
b) Tìm số vi khuẩn còn sống trước lần sử dụng thứ năm.
Bài 13 :
Tính tổng 6 số hạng đầu của dãy số \(\left( {{u_n}} \right)\), biết \({u_n} = 3n - 1\).
Bài 14 :
Trong mặt phẳng toạ độ \(Oxy\), cho hàm số \(y = \frac{{2x - 1}}{{2{x^2} + 1}}\) có đồ thị \(\left( C \right)\). Với mỗi số nguyên dương \(n\), gọi \({A_n}\) là giao điểm của đồ thị \(\left( C \right)\) với đường thẳng \(x = n\). Xét dãy số \(\left( {{u_n}} \right)\) biết \({u_n}\) là tung độ của \({A_n}\). Hãy tìm công thức của số hạng tổng quát \({u_n}\).
Bài 15 :
Cho dãy số \(\left( {{u_n}} \right)\), biết \({u_n} = \sin \left[ {\left( {2n - 1} \right)\frac{\pi }{4}} \right]\).
a) Viết bốn số hạng đầu của dãy số.
b) Chứng minh rằng \({u_{n + 4}} = {u_n}\) với mọi \(n \ge 1\).
c) Tính tổng 12 số hạng đầu của dãy số.
Bài 16 :
Với mỗi số nguyên dương \(n\), lấy \(n + 6\) điểm cách đều nhau trên đường tròn. Nối mỗi điểm với điểm cách nó hai điểm trên đường tròn đó để tạo thành các ngôi sao như hình vẽ. Gọi \({u_n}\) là số đo góc ở đỉnh tính theo đơn vị độ của mỗi ngôi sao thì ta được dãy số \(\left( {{u_n}} \right)\). Tìm công thức của số hạng tổng quát \({u_n}\).
Bài 17 :
Cho dãy số (\({u_n}\)) xác định bởi \({u_1} = 1,\,\,{u_{n + 1}} = {u_n} + n\). Số hạng \({u_4}\)là:
A. 5
B. 6
C. 7
D. 10.
Bài 18 :
Cho dãy số \({u_n} = 2020\sin \frac{{n\pi }}{2} + 2021\cos \frac{{n\pi }}{3}\). Mệnh đề nào dưới đây là đúng?
A.\({u_{n + 6}} = {u_n}\)
B.\({u_{n + 9}} = {u_n}\)
C. \({u_{n + 4}} = {u_n}\)
D. \({u_{n + 12}} = {u_n}\).
Bài 19 :
Cho dãy số \(\left( {{u_n}} \right)\) biết \({u_1} = 2\), \({u_n} = \frac{1}{3}\left( {{u_{n - 1}} + 1} \right)\) với \(n \ge 2\). Số hạng \({u_4}\) bằng:
A. \({u_4} = 1\)
B. \({u_4} = \frac{2}{3}\)
C. \({u_4} = \frac{{14}}{{27}}\)
D. \({u_4} = \frac{5}{9}\)
Bài 20 :
Cho dãy số \(\left( {{u_n}} \right)\) biết \({u_n} = \cos \left[ {\left( {2n + 1} \right)\frac{\pi }{6}} \right]\)
a) Viết sáu số hạng đầu của dãy số.
b) Chứng minh rằng \({u_{n + 6}} = {u_n}\) với mọi \(n \ge 1\)
c) Tính tổng 27 số hạng đầu của dãy số.
Bài 21 :
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{n + 1}}{{2n + 1}}\). Số \(\frac{8}{{15}}\) là số hạng thứ bao nhiêu của dãy số?
Bài 22 :
Cho dãy số \(\left( {{u_n}} \right)\) xác định bởi \(\left\{ \begin{array}{l}{u_1} = 4\\{u_{n + 1}} = {u_n} + n\left( {n \ge 1} \right)\end{array} \right.\). Tìm số hạng thứ năm của dãy số đó.
Bài 23 :
Cho dãy số $\left( {{u_n}} \right)$ có ${u_n} = \frac{{2n}}{{{n^2} + 1}}$. Số $\frac{9}{{41}}$ là số hạng thứ bao nhiêu của dãy số $\left( {{u_n}} \right)$?
-
A.
10.
-
B.
9.
-
C.
8.
-
D.
11.


















Danh sách bình luận