Cho tam giác ABC, trung tuyến AI. Tia phân giác góc AIB cắt AB tại M và tia phân giác góc AIC cắt AC tại N. Chứng minh rằng: MN // BC.
Dựa vào tính chất đường phân giác của tam giác và định lí Thales đảo.

∆AIB có IM là phân giác của \(\widehat {AIB}\) nên \(\frac{{AM}}{{MB}} = \frac{{AI}}{{IB}}\) (tính chất đường phân giác trong tam giác). (1)
∆AIC có IN là phân giác của \(\widehat {AIC}\) nên \(\frac{{AN}}{{NC}} = \frac{{AI}}{{IC}}\) (tính chất đường phân giác trong tam giác). (2)
IB = IC (I là trung điểm BC). (3)
Từ (1), (2), (3), ta có: \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}.\) Suy ra MN // BC (định lí Thales đảo).

Các bài tập cùng chuyên đề
Bài 1 :
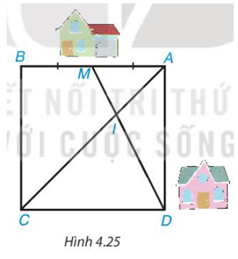
Nhà bạn Mai ở vị trí M, nhà bạn Dung ở vị trí D (Hình 4.25), biết rằng tứ giác ABCD là hình vuông và M là trung điểm của AB. Hai bạn đi bộ với cùng một vận tốc trên con đường MD để đến điểm I. Bạn Mai xuất phát lúc 7h. Hỏi bạn Dung xuất phát lúc mấy giờ để gặp bạn Mai lúc 7h30 tại điểm I?
Bài 2 :
Tam giác ABC có AB = 15 cm, AC = 20 cm, BC = 25 cm. Đường phân giác của góc BAC cắt BC tại D.
a) Tính độ dài đoạn thẳng DB và DC.
b) Tính tỉ số diện tích của hai tam giác ABD và ACD.
Bài 3 :
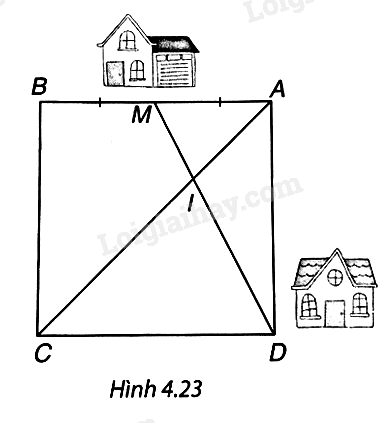
Nhà bạn Mai ở vị trí M, nhà bạn Dung ở vị trí D (H.4.23), biết rằng tứ giác ABCD là hình vuông và M là trung điểm của AB. Hai bạn đi bộ với cùng một vận tốc trên con đường MD để đến điểm I. Bạn Mai xuất phát lúc 7h. Hỏi bạn Dung xuất phát lúc mấy giờ để gặp bạn Mai lúc 7h30 tại điểm I?
Bài 4 :
Tam giác \(ABC\) có \(AB = 15cm,AC = 20cm,BC = 25cm\). Đường phân giác của góc \(BAC\)cắt \(BC\) tại \(D\). Qua \(D\) vẽ \(DE//AB\left( {E \in AC} \right)\).
a) Tính độ dài các đoạn thẳng \(BD,DC\) và \(DE\).
b) Chứng minh \(ABC\) là tam giác vuông. Tính diện tích tam giác \(ABC\).
c) Tính diện tích tam giác \(ADB,ADE\) và \(DCE\).
Bài 5 :
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 3cm,AC = 4cm.\) Đường phân giác của góc \(A\) cắt \(BC\) tại \(D\).
a) Tính \(BC,BD,DC\).
b) Vẽ đường cao \(AH\). Tính \(AH,HD\) và \(AD\).
Bài 6 :
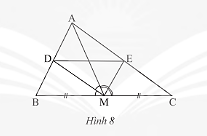
Cho tam giác \(ABC\) có đường trung tuyến \(AM\). Đường phân giác của góc \(AMB\) cắt \(AB\) tại \(D\) và đường phân giác góc \(AMC\) cắt \(AC\) tại \(E\) (Hình 8). Chứng minh \(DE//BC\).
Bài 7 :
Cho tam giác ABC có đường trung tuyến AM \(\left( {M \in BC} \right)\). Tia phân giác của góc AMB cắt AB tại D, tia phân giác của góc AMC cắt AC tại E.
a) Chứng minh DE//BC.
b) Gọi I là giao điểm của DE với AM. Chứng minh I là trung điểm của DE.


















Danh sách bình luận