Cho hình vuông \(ABCD\) có \(AB = 12cm\). Trên cạnh \(CD\) lấy điểm \(E\) sao cho \(DE = 5cm\). Tia phân giác của góc \(BAE\) cắt \(BC\) tại \(F\). Trên tia đối của tia \(BC\) lấy điểm \(M\) sao cho \(BM = DE\).
a) Chứng minh \(AE = AM = DE\)
b) Tính độ dài \(BF\).
Trong một hình vuông,
- Các cạnh đối song song
- Hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
- Hai đường chéo là các đường phân giác của các góc ở đỉnh.
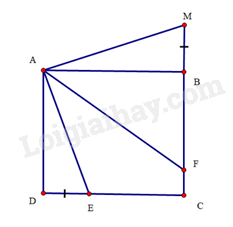
a) \(\Delta ADE = \Delta ABM\)(c.g.c)
Suy ra \(AE = AM\) và \(\widehat {DAE} = \widehat {BAM}\).
Do \(AF\) là tia phân giác của \(\widehat {BAE}\) nên \(\widehat {EAF} = \widehat {BAF}\).
Suy ra \(\widehat {DAE} + \widehat {EAF} = \widehat {BAM} + \widehat {BAF}\) hay \(\widehat {DAF} = \widehat {MAF}\).
Mà \(\widehat {DAF} = \widehat {MFA}\) (hai góc so le trong) , suy ra \(\widehat {MFA} = \widehat {MAF}\)
Do đó, tam giác \(MAF\) cân tại \(M\). Suy ra \(AM = FM\)
Mà \(AE = AM\), suy ra \(AE = AM = FM\).
b) Trong tam giác \(ADE\) vuông tại \(D\), ta có: \(A{E^2} = A{D^2} + D{E^2}\)
Suy ra \(AE = 13cm\). Mà \(FM = AE\), suy ra \(FM = 13cm\).
Ta có: \(FM = BM + BF\). Mà \(BM = DE = 5cm\) và \(FM = 13cm\), suy ra \(BF = 8cm\).

Các bài tập cùng chuyên đề
Bài 1 :
Hãy giải thích tại sao hai đường chéo của hình vuông bằng nhau và vuông góc với nhau.
Bài 2 :
Cho tứ giác \(ABCD\) có bốn góc bằng nhau và có bốn cạnh bằng nhau. Hãy chứng tỏ \(ABCD\) vừa là hình thoi vừa là hình thoi vừa là hình chữ nhật.
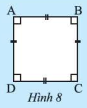
Bài 3 :
Cho hình vuông \(MNPQ\). Chứng minh \(MNPQ\) vừa là hình chữ nhật vừa là hình thoi.
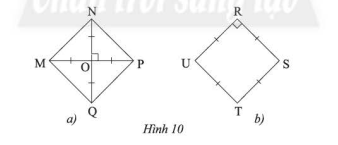
Bài 4 :
Tìm hình vuông trong hai hình sau:
Bài 5 :
Tìm bốn ví dụ về hình vuông trong thực tế
Bài 6 :
Cho biết các góc và các cạnh của tứ giác ABCD ở Hình 65 có đặc điểm gì?
Bài 7 :
Em hãy mô tả cạnh và góc của một tứ giác vừa là hình chữ nhật, vừa là hình thoi.
Bài 8 :
Cho hình vuông \(ABCD\). Lấy điểm \(E\) thuộc cạnh \(CD\) và điểm \(F\) thuộc tia đối của tia \(BC\) sao cho \(BF = DE\).
a) Chứng minh tam giác \(AEF\) là tam giác vuông cân
b) Gọi \(I\) là trung điểm của \(EF\). Trên tia đối của tia \(IA\) lấy điểm \(K\) sao cho \(IK = IA\). Chứng minh tứ giác \(AEKF\) là hình vuông.
c) Chứng minh \(I\) thuộc đường thẳng \(BD\).



















Danh sách bình luận