Cho hình chữ nhật \(ABCD\) có hai cạnh kề không bằng nhau. Tia phân giác của các góc \(A\) và \(B\) cắt nhau tại \(E\). Tia phân giác của các góc \(C\) và \(D\) cắt nhau tại \(F\). Gọi \(G\) là giao điểm của \(AE\) và \(DF\), \(H\) là giao điểm của \(BE\) và \(CF\). Chứng minh:
a) \(GH//CD\)
b) Tứ giác \(GFHE\) là hình vuông
Dựa vào dấu hiệu nhận biết của hình vuông:
- Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông
- Hình chữ nhật có hai đường chéo là đường phân giác của một góc là hình vuông
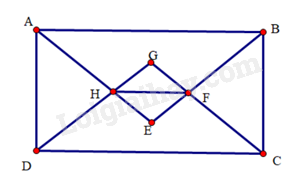
a) Do \(ABCD\) là hình chữ nhật nên \(\widehat {DAB} = \widehat {ABC} = \widehat {BCD} = \widehat {CDA} = 90^\circ \)
Mà \(AE,BE,CF,DF\) lần lượt là các tia phân giác của các góc \(DAB,ABC,BCD,CDA\) suy ra \(\widehat {DAE} = \widehat {EAB} = \widehat {ABE} = \widehat {EBC} = \widehat {BCF} = \widehat {FCD} = \widehat {CDF} = \widehat {FDA} = 45^\circ \)
Do đó, các tam giác \(EAB,FCD,GAD,HBC\) đều là tam giác vuông cân.
\(\Delta GAD = \Delta HBC\) (g.c.g). Suy ra \(GD = HC\). Mà \(FD = FC\), suy ra \(FG = FH\).
Do đó, tam giác \(FGH\) vuông cân tại \(F\). Suy ra \(\widehat {FGH} = 45^\circ \).
Ta có: \(\widehat {FGH} = \widehat {CDF} = 45^\circ \) và \(\widehat {FGH},\widehat {CDF}\) nằm ở vị trí đồng vị nên \(GH//CD\).
b) \(\widehat {EGF} = \widehat {AGD} = 90^\circ \) (hai góc đối đỉnh)
Tứ giác \(GFHE\) là hình chữ nhật.
Hình chữ nhật \(GFHE\) có \(FG = FH\) nên \(GFHE\) là hình vuông.

Các bài tập cùng chuyên đề
Bài 1 :
Cho hình vuông ABCD. M là điểm nằm trong hình vuông. Gọi E, F lần lượt là hình chiếu của M trên cạnh AB và AD. Tứ giác AEMF là hình vuông khi
-
A.
M trên đường chéo AC
-
B.
M thuộc cạnh DC
-
C.
M thuộc đường chéo BD
-
D.
M tùy ý nằm trong hình vuông ABCD
Bài 2 :
Cho tam giác ABC vuông tại A. Gọi M, N, P lần lượt là các trung điểm của AB, BC, AC và \(AM = \frac{1}{2}AB{;^{}}AP = \frac{1}{2}AC\). Tam giác ABC cần có thêm điều kiện gì để hình chữ nhật AMNP là hình vuông?
-
A.
\(AB = \frac{1}{2}AC\)
-
B.
\(AB = AC\)
-
C.
\(AC = \frac{1}{2}AB\)
-
D.
\(\widehat B = {60^o}\)
Bài 3 :
Hãy viết giả thiết, kết luận của câu a trong Định lí 4.
Bài 4 :
Với mỗi hình dưới đây, ta dùng dấu hiệu nhận biết nào để khẳng định đó là hình vuông?
Bài 5 :
Lấy một tờ giấy, gấp làm tư tạo ra một góc vuông O, đánh dấu hai điểm A, B trên hai cạnh góc vuông rồi cắt theo đoạn thẳng AB (H.3.46a). Sau khi mở tờ giấy ra, ta được một tứ giác. Tứ giác đó là hình gì? Vì sao? Nếu ta có OA = OB thì tứ giác nhận được là hình gì (H.3.46b)?
Hãy giải thích tại sao.
- Trong trường hợp a, ta được hình thoi.
- Trong trường hợp b, ta được hình vuông
Bài 6 :
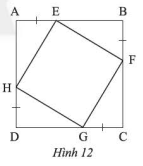
Trong Hình 12, cho biết \(ABCD\) là một hình vuông. Chứng minh rằng:
a) Tứ giác \(EFGH\) có ba góc vuông
b) \(HE = HG\)
c) Tứ giác \(EFGH\) là một hình vuông
Bài 7 :
Bạn Nam kiểm tra mặt kính của chiếc đồng hồ để bàn và nhận thấy có ba góc vuông và hai cạnh kề bằng nhau (Hình 13). Hãy cho biết mặt kính đồng hồ có hình gì?

Bài 8 :
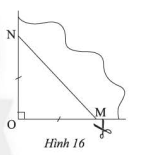
Lấy một tờ giấy, gấp làm tư để có một góc vuông như triong Hình 16, dùng kéo cắt theo đường \(MN\) sao cho \(OM = ON\). Mở phần giấy cắt được ra ta được một tứ giác. Tứ giác đó là hình gì. Giải thích kết luận của em.
Bài 9 :
Trong các khẳng định sau, khẳng định nào đúng?
A. Hình chữ nhật có hai đường chéo bằng nhau là hình vuông
B. Hình thoi có hai đường chéo vuông góc là hình vuông
C. Hình thoi có một góc vuông là hình vuông
D. Hình chữ nhật có một góc vuông là hình vuông
Bài 10 :
a) Cho hình chữ nhật ABCD có hai cạnh kề AB và BC bằng nhau. ABCD có phải là hình vuông hay không?
b) Cho hình chữ nhật ABCD có hai đường chéo AC và BD vuông góc với nhau (hình 69)
- Đường thẳng AC có phải là đường trung trực của đoạn thẳng BD hay không?
- ABCD có phải là hình vuông hay không?
c) Cho hình chữ nhật ABCD có AC là tia phân giác của góc DAB
- Tam giác ABC có phải là tam giác vuông cân hay không?
- ABCD có phải là hình vuông hay không?
Bài 11 :
Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy điểm D, E sao cho: BD = DE = EC
Qua D và E kẻ đường thẳng vuông góc với BC, chúng cắt AB và AC lần lượt tại H và G. Chứng minh tứ giác DEGH là hình vuông.
Bài 12 :
Cho hình thoi ABCD có AC = BD. Chứng minh ABCD là hình vuông.
Bài 13 :
Cho hình thoi ABCD có \(\widehat A = {90^o}\). Chứng minh ABCD là hình vuông.
Bài 14 :
Cho tam giác ABC vuông tại A có đường phân giác AD. Gọi H, K lần lượt là hình chiếu của D trên AB, AC. Chứng minh tứ giác AHDK là hình vuông.
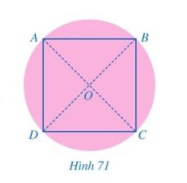
Bài 15 :
Bạn Thảo có một mảnh giấy có dạng hình tròn. Bạn Thảo đố bạn Minh: Không dùng thước thẳng và compa, làm thế nào có thể xác định tâm của hình tròn và chọn ra 4 vị trí trên đường tròn đó để chúng là 4 đỉnh của một hình vuông?
Bạn Minh làm như sau:
Bước 1: Gấp mảnh giấy sao cho hai nửa đường tròn trùng khít nhau. Nét gấp thẳng tạo thành đường kính của hình tròn. Ta đánh dấu hai đầu mút của đường kính đó là hai điểm A, C.
Bước 2: Tiếp tục gấp mảnh giấy (có dạng nửa hình tròn) ở Bước 1 sao cho hai nửa hình tròn đó lại trùng khít nhau. Trải miếng bìa về dạng hình tròn bạn đầu, ta được nét gấp mới là một đường kính khác của hình tròn.
Bước 3: Ta đánh dấu giao điểm của hai đường kính là O và hai đầu mút của đường kính mới là hai điểm B, D. Khi đó O là tâm của hình tròn và tứ giác ABCD là hình vuông (Hình 71)
Em hãy giải thích cách làm của bạn Minh.
Bài 16 :
Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm M, N, P, Q sao cho AM = BN = CP = DQ < AB. Chứng minh tứ giác MNPQ là hình vuông.
Bài 17 :
1. Từ dấu hiệu nhận biết hình thoi, em hãy bổ sung thêm một điều kiện để một hình chữ nhật là hình vuông.
2. Từ dấu hiệu nhận biết hình chữ nhật, em hãy bổ sung một điều kiện để một hình thoi là hình vuông.
Bài 18 :
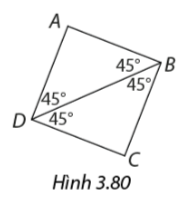
Tứ giác ABCD trong hình 3.80 có là hình vuông không? Vì sao?
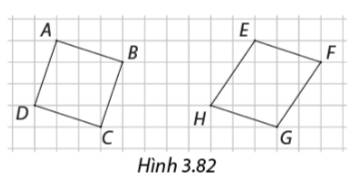
Bài 19 :
Tứ giác trong hình 3.82 là hình vuông? Vì sao?
Bài 20 :
Cho tam giác ABC cân tại A \(\left( {\widehat A < {{90}^0}} \right)\), các đường cao BD và CE cắt nhau tại H. Tia phân giác của góc ABD cắt EC và AC lần lượt tại M và P. Tia phân giác của góc ACE cắt BD và AB lần lượt tại Q và N. Chứng minh rằng:
a) \(\widehat {ABD} = \widehat {ACE}\);
b) \(BH = CH;\)
c) Tam giác BOC vuông cân;
d) MNPQ là hình vuông.
Bài 21 :
Cho tam giác ABC vuông tại A. Trên cạnh AB lấy điểm K, trên cạnh AC lấy điểm H sao cho BK = CH. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh KH, BH, BC, CK. Chứng minh rằng MNPQ là hình vuông.
Bài 22 :
Xét tam giác ABC vuông cân tại A. Lấy trên cạnh BC hai điểm D, E sao cho \(BD = DE = EC\). Lấy các điểm F, G lần lượt thuộc cạnh AC, AB sao cho FE, GD vuông góc với BC. Chứng minh tứ giác DEFG là một hình vuông.
Bài 23 :
Cho hình vuông \(ABCD\) có hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\). Trên tia đối của tia \(CB\) lấy điểm \(K\) sao cho \(BC = CK\). Từ điểm \(B\) kẻ đường thẳng song song với \(AC\) cắt tia \(DC\) tại \(E\). Gọi \(F\) là trung điểm của \(BE\).
a) Chứng minh các tứ giác \(BOCF\) và \(BDKE\) đều là hình vuông.
b) Tứ giác \(CDOF\) có thể là hình vuông không? Vì sao?
Bài 24 :
Hình thoi cần thêm yếu tố nào để trở thành hình vuông?
-
A.
Hai đường chéo vuông góc.
-
B.
Có một góc vuông.
-
C.
Hai cạnh kề bằng nhau.
-
D.
Một đường chéo là tia phân giác của một góc.
Bài 25 :
Nhận định nào sau đây là sai?
-
A.
Hình vuông là hình chữ nhật có hai cạnh bên bằng nhau.
-
B.
Hình vuông có hai đường chéo bằng nhau và vuông góc với nhau.
-
C.
Hình vuông có hai đường chéo là phân giác các góc ở đỉnh của hình vuông.
-
D.
Hình vuông là hình chữ nhật nhưng không là hình thoi.
Bài 26 :
Cho các hình vẽ sau:
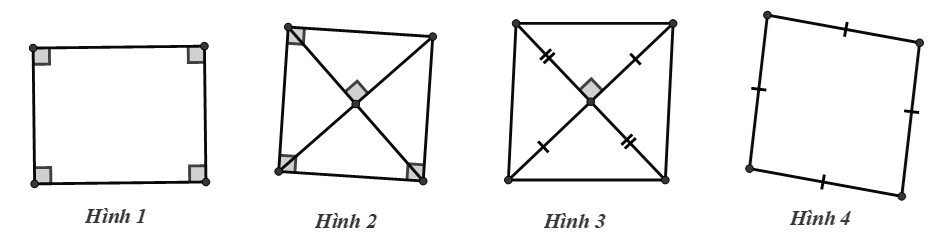
Trong các hình sau, những hình nào là hình vuông?
-
A.
Hình 1.
-
B.
Hình 2.
-
C.
Hình 3.
-
D.
Hình 4.
Bài 27 :
Các dấu hiệu nhận biết sau, dấu hiệu nào không đủ để kết luận một hình vuông?
-
A.
Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
-
B.
Hình thoi có một góc vuông là hình vuông.
-
C.
Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.
-
D.
Hình thoi có hai đường chéo vuông góc là hình vuông.
Bài 28 :
Để chứng minh tứ giác \(ABCD\) là hình vuông, dấu hiệu nào sau đây là sai?
-
A.
Tứ giác \(ABCD\) là hình thoi có hai đường chéo bằng nhau.
-
B.
Tứ giác \(ABCD\) là hình thoi có một góc vuông.
-
C.
Tứ giác \(ABCD\) là hình thoi có hai đường chéo vuông góc
-
D.
Tứ giác \(ABCD\) là hình chữ nhật có hai cạnh kề bằng nhau.
Bài 29 :
Cho hình vuông \(ABCD\). Trên cạnh \(AB\), \(BC\), \(CD\), \(DA\) lần lượt lấy các điểm \(E\), \(F\), \(G\), \(H\) sao cho \(AE = BF = CG = DH\). Tứ giác \(EFGH\) là hình gì?
-
A.
Hình bình hành.
-
B.
Hình chữ nhật.
-
C.
Hình thoi.
-
D.
Hình vuông.
Bài 30 :
Cho hình chữ nhật \(ABCD\) có \(AB = 2AD\). Gọi \(E, F\) theo thứ tự là trung điểm của \(AB, CD\); \(EF\parallel AD\parallel BC\). Gọi \(M\) là giao điểm của \(AF\) và \(DE\), \(N\) là giao điểm của \(BF\) và \(CE\). Tứ giác \(EMFN\) là hình gì?
-
A.
Hình bình hành.
-
B.
Hình chữ nhật.
-
C.
Hình thoi.
-
D.
Hình vuông.



















Danh sách bình luận