Cho tam giác \(ABC\) vuông cân tại \(A\). Lấy điểm \(M\) thuộc cạnh huyền \(BC\). Gọi \(D,E\) lần lượt là hình chiếu của điểm \(M\) trên đường thẳng \(AB,AC\).
a) Tứ giác \(ADME\) là hình gì? Vì sao?
b) Gọi \(I\) là trung điểm của \(DE\). Chứng minh ba điểm \(A,I,M\) thẳng hàng
c) Chứng minh khi điểm \(M\) thay đổi vị trí trên cạnh \(BC\) thì chu vi của tứ giác \(ADME\) không đổi.
Dựa vào tính chất của hình chữ nhật:
- Hai cạnh đối song song và bằng nhau
- Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường
Và dựa vào định lí Pythagore: trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

a) Tứ giác \(ADME\) có \(\widehat {DAE} = \widehat {AEM} = \widehat {MDA} = 90^\circ \) nên \(ADME\) là hình chữ nhật.
b) Do \(ADME\) là hình chữ nhật nên hai đường chéo \(DE\) và \(AM\) cắt nhau tại trung điểm của mỗi đường.
Mà \(I\) là trung điểm của \(DE\), suy ra \(I\) là trung điểm của \(AM\). Vậy ba điểm \(A < I,M\) thẳng hàng.
c) Do \(ADME\) là hình chữ nhật nên \(DM//AC\). Suy ra \(\widehat {BMD} = \widehat {ACB}\) (hai góc so le trong). Mà \(\widehat {ABC} = \widehat {ACB} = 45^\circ \) (vì tam giác \(ABC\) vuông cân tại \(A\), suy ra \(\widehat {BMD} = \widehat {ABC} = 45^\circ \). Do đó, tam giác \(BDM\) cân tại \(D\). Suy ra \(BD = DM\).
Chu vi hình chữ nhật \(ADME\) là: \(2\left( {AD + DM} \right) = 2\left( {AD + BD} \right) = DM\)
Mà \(AB\) không đổi nên chu vi của tứ giác \(ADME\) không đổi.
d)

Do \(ADME\) là hình chữ nhật nên \(AM = DE\)
Suy ra \(DE\) có độ dài nhỏ nhất khi \(AM\) có độ dài nhỏ nhất. vậy \(M\) là hình chiếu của \(A\) trên đường thẳng \(BC\).
Trong tam giác \(ABC\) vuông cân tại \(A\) ta cóL
\(AC = AB = 2cm\) và \(B{C^2} = A{B^2} + A{C^2} = 8\)
Suy ra \(BC = \sqrt 8 cm\)
\(\Delta ABM = \Delta ACM\) (cạnh góc vuông – góc nhọn). Suy ra \(BM = CM = \frac{{BC}}{2} = \sqrt 2 cm\)
Tam giác \(ABM\) vuông tại \(M\) có \(\widehat {ABM} = 45^\circ \) nên \(\widehat {BAM} = \widehat {ABM} = 45^\circ \). Suy ra tam giác \(ABM\) vuông cân tại \(M\). Do đó \(AM = BM = \sqrt 2 cm\). Vậy \(DE = \sqrt 2 cm\).

Các bài tập cùng chuyên đề
Bài 1 :
Cho hình bình hành ABCD có góc A vuông. Tính các góc B, C, D. Tứ giác ABCD có là hình chữ nhật không? Vì sao?
Bài 2 :
Cho tứ giác ABCD có \(\widehat A = {90^o}\), hai đường chéo cắt nhau tại trung điểm O của mỗi đường. Hỏi tứ giác ABCD là hình gì? Tại sao?
Bài 3 :
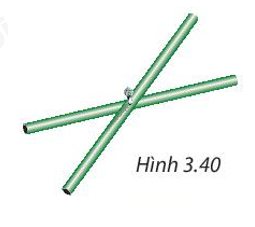
Hai thanh tre thẳng bằng nhau, được gắn với nhau tại trung điểm của mỗi thanh. Khi các đầu mút của hai thanh tre đó tạo thành bốn đỉnh của một tứ giác (H.3.40) thì tứ giác đó là hình gì? Tại sao?
Bài 4 :
Cho tam giác ABC, đường cao AH. Gọi M là trung điểm của AC, N là điểm sao cho M là trung điểm của HN. Chứng minh tứ giác AHCN là hình chữ nhật.
Bài 5 :
Gọi Ou và Ov lần lượt là hai tia phân giác của hai góc kề bù xOy và x’Oy; A là một điểm khác O trên tia Ox. Gọi B và C là chân đường vuông góc hạ từ A lần lượt xuống đường thẳng chứa Ou và Ov. Hỏi tứ giác OBAC là hình gì? Vì sao?
Bài 6 :
Cho hình bình hành \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Giải thích các khẳng định sau:
a) Nếu \(\widehat {{\rm{BAD}}}\) là góc vuông thì \(\widehat {{\rm{ADC}}}\) và \(\widehat {{\rm{ABC}}}\) cũng là góc vuông.
b) Nếu \(AC = BD\) thì \(\widehat {{\rm{BAD}}}\) vuông.
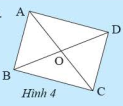
Bài 7 :
Chỉ được sử dụng compa, hãy kiểm tra tứ giác có phải là hình chữ nhật hay không.

Bài 8 :
a) Hãy sử dụng ê ke sao cho chỉ sau ba lần đo ta có thể xác định khung cửa sổ ở Hình 7 có phải là hình chữ nhật hay không?
b) Hãy sử dụng một cuộn dây, xác định khung cửa sổ trong Hình 7 có là hình chữ nhật hay không?

Bài 9 :
Cho tam giác \(ABC\) có đường cao \(AH\). Gọi \(I\) là trung điểm của \(AC\), \(E\) là điểm đối xứng với \(H\) qua \(I\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(HC\), \(CE\). Các đường thẳng \(AM\), \(AN\) cắt \(HE\) tại \(G\) và \(K\).
a) Chứng minh tứ giác \(AHCE\) là hình chữ nhật
b) Chứng minh \(HG = GK = KE\)
Bài 10 :
a) Cho hình bình hành ABCD có \(\widehat A = {90^o}\). ABCD có phải là hình chữ nhật hay không?
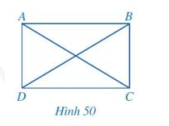
b) Cho hình bình hành ABCD có hai đường chéo AC và BD bằng nhau (hình 50)
Hai tam giác ABC và DCB có bằng nhau hay không? Từ đó, hãy so sánh \(\widehat {ABC}\) và \(\widehat {DCB}\).
ABCD có phải là hình chữ nhật hay không?
Bài 11 :
Cho hình bình hành ABCD có hai đường chéo AC và BD cắt nhau tại O thỏa mãn \(\widehat {OAB} = \widehat {O{\rm{D}}C}\). Chứng minh ABCD là hình chữ nhật.
Bài 12 :
Cho hình thang cân ABCD có AB // CD, \(\widehat A = {90^o}\). Chứng minh ABCD là hình chữ nhật.
Bài 13 :
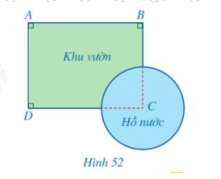
Một khu vườn có dạng tứ giác ABCD với các góc A, B, D là góc vuông, AB = 400 m, AD = 300 m. Người ta đã làm một cái hồ nước có dạng hình tròn, khi đó vị trí C không còn nằm trong khu vườn nữa (hình 52). Tính khoảng cách từ vị trí C đến mỗi vị trí A, B, D.
Bài 14 :
Bạn Linh có một mảnh giấy dạng hình tròn. Bạn Linh đó bạn Bình: làm thế nào có thể chọn ra 4 vị trí trên đường tròn đó để chúng là 4 đỉnh của một hình chữ nhật?
Bạn Bình làm như sau:
Bước 1: gấp mảnh giấy sao cho hai nửa đường tròn trùng khít nhau. Nét gấp thẳng tạo thành đường kính của hình tròn. Ta đánh dấu đầu mút của đường kính đó hai điểm A, C.
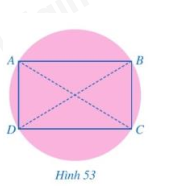
Bước 2: Sau đó lại gấp tương tự mảnh giấy đó nhưng theo đường kính mới và đánh dấu hai đầu mút của đường kính mới là hai điểm B, D. Khi đó tứ giác ABCD là hình chữ nhật (hình 53)
Em hãy giải thích cách làm của bạn Bình.
Bài 15 :
Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lần lượt lấy các điểm D, G sao AD = CG < AC. Từ điểm D kẻ DE vuông góc với AC (E thuộc AB). Chứng minh tứ giác CDEG là hình chữ nhật.
Bài 16 :
1. Trong Hình 3.55, tầng trên của khay đựng giấy được gắn với tầng dưới bởi hai thanh AD, BC với \(AB = DC,AD = BC.\) Ta có thể đưa tầng trên của khay ra trước hoặc về sau bằng cách thay đổi góc ADC. Em hãy cho biết:
a) Tứ giác ABCD luôn là hình gì?
b) Khi góc ADC bằng bao nhiêu độ thì ABCD là hình chữ nhật?

2. Giải thích câu trả lời ở trên của em bằng cách tính các góc hình bình hành ABCD nếu \(\widehat {ADC} = 90^\circ \)(Hình 3.55b).
Bài 17 :
1. Trong hình 3.56, hình bình hành ABCD có đường chéo BD cố định, còn AC có thể thay đổi bằng cách di chuyển điểm C trên tia Dx. Độ dài AC như thế nào so với BD thì ABCD là hình chữ nhật?

2. Dựa vào tính chất và dấu hiệu nhận biết hình thang cân, em hãy giải thích vì sao khi \(AC = BD\) thì hình bình hành ABCD có bốn góc bằng nhau. Tính số đo mỗi góc và cho biết khi đó ABCD là hình gì?
Bài 18 :
1. Trong Hình 3.57, khi hai bên nắp hộp được mở đều về hai phía, mép AD và BC của hai nắp là hai cạnh bên của một hình thang cân. Góc ADC như thế nào thì ABCD là hình chữ nhật?
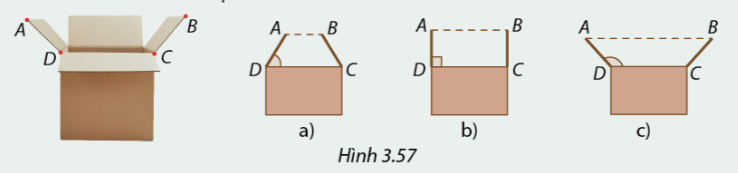
2. Giải thích câu trả lời ở trên của em bằng cách tính các góc của hình thang cân ABCD nếu \(\widehat {ADC} = 90^\circ \).(Hình 3.57b)
Bài 19 :
Trong hình 3.59, Hình bình hành nào là hình chữ nhật?

Bài 20 :
Trong Hình 3.60, mặt ABCD của thùng gỗ được gia cố bằng hai thanh gỗ AC và BD. Chỉ dùng thước đo độ dài, bác thợ mộc có thể khẳng định các góc A, B, C, D của mặt thùng đều vuông. Em hãy cho biết bác đã làm cách nào.

Bài 21 :
Giải thích vì sao các tứ giác trong hình 3.63 là hình chữ nhật.
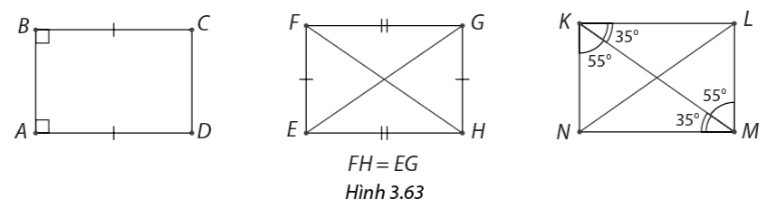
Bài 22 :
Cho đường tròn tâm O có AC và BD là hai đường kính phân biệt. Tứ giác ABCD là hình gì?
Bài 23 :
Cho hình thang ABCD có \(\widehat A = \widehat D = {90^0},AB = 3cm,AD = 4cm\) và \(CD = 6cm\)(hình 3.64). Tính độ dài cạnh BC.

Bài 24 :
Hãy chọn phương án sai.
A. Tứ giác có ba góc vuông là hình chữ nhật.
B. Hình bình hành có một góc vuông là hình chữ nhật.
C. Hình thang cân có hai đường chéo bằng nhau là hình chữ nhật.
D. Hình chữ nhật có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Bài 25 :
Bằng ê ke, nêu cách kiểm tra một tứ giác có là hình chữ nhật hay không. Hãy giải thích kết quả.
Bài 26 :
Bằng compa, nêu cách kiểm tra một tứ giác có là hình chữ nhật hay không. Giải thích kết quả.
Bài 27 :
Cho tam giác ABC, đường cao AH. Gọi M là trung điểm của AC, N là điểm sao cho M là trung điểm của HN. Chứng minh tứ giác AHCN là hình chữ nhật.
Bài 28 :
Cho hình bình hành ABCD. Các tia phân giác của góc A, B, C, D cắt nhau như trên Hình 3.39.

Chứng minh rằng EFGH là hình chữ nhật.
Bài 29 :
Gọi Ou và Ov lần lượt là hai tia phân giác của hai góc kề bù xOy và x’Oy; A là một điểm khác O trên tia Ox. Gọi B và C là chân đường vuông góc hạ từ A lần lượt xuống đường thẳng chứa Ou và Ov. Hỏi tứ giác OBAC là hình gì? Vì sao?
Bài 30 :
Hai đường trung tuyến BM, CN của tam giác ABC cân tại A cắt nhau tại G. Gọi H, K lần lượt là điểm sao cho trung điểm của GH là M, trung điểm của GK là N. Chứng minh tứ giác BCHK là hình chữ nhật.


















Danh sách bình luận