Cho hình chữ nhật ABCD có \(AB = 2BC\). Gọi I là trung điểm của AB và K là trung điểm của CD. Chứng minh:
a) AIKD và BIKC là hình vuông.
b) \(IK = \frac{{DC}}{2}\) và \(\widehat {DIC} = {90^0}\).
a) Sử dụng kiến thức về dấu hiệu nhận biết hình vuông để chứng minh: Hình thoi có một góc vuông là hình vuông.
b) Sử dụng kiến thức về tính chất của hình vuông để chứng minh: Trong hình vuông:
+ Các đường chéo là các đường phân giác của các góc hình vuông
+ Có 4 góc vuông.
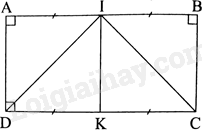
a) Vì I là trung điểm của AB nên \(AI = IB = \frac{1}{2}AB\)
Vì K là trung điểm của CD nên \(DK = CK = \frac{1}{2}DC\)
Vì ABCD là hình chữ nhật nên AB//CD, \(AB = CD\), \(AD = BC\)
Do đó, \(IA = IB = DK = CK\)
Mà \(AB = 2BC\) nên \(IA = IB = DK = CK = AD = BC\)
Tứ giác AIKD có: \(DK = AI\), AI//DK nên AIKD là hình bình hành. Mà \(IA = AD\) nên AIKD là hình thoi. Lại có \(\widehat A = {90^0}\) nên AIKD là hình vuông.
Tứ giác BIKC có: \(IB = KC\), BI//CK nên BIKC là hình bình hành. Mà \(IB = BC\) nên BIKC là hình thoi. Lại có \(\widehat B = {90^0}\) nên BIKC là hình vuông.
b) Vì AIKD là hình vuông nên \(IK = DK = \frac{{DC}}{2}\) và \(\widehat {IDC} = \frac{1}{2}\widehat {ADC} = {45^0}\)
Vì BIKC là hình vuông nên \(\widehat {DCI} = \frac{1}{2}\widehat {DCB} = {45^0}\)
Tam giác DIC có: \(\widehat {DIC} = {180^0} - \widehat {DCI} - \widehat {CDI} = {90^0}\)
Các bài tập cùng chuyên đề
Một số họa tiết và hoa văn trên thổ cẩm (Hình 64) có dạng hình vuông
Hình vuông có những tính chất gì? Có những dấu hiệu nào để nhận biết một tứ giác là hình vuông?
Cho hai mảnh giấy, mỗi mảnh có dạng hình vuông với độ dài 1dm. Hãy trình bày cách cắt ghép hai mảnh giấy đó để được một hình vuông có độ dài cạnh là \(\sqrt 2 dm\).
Một mặt bánh chưng có dạng hình vuông ABCD được cắt theo bốn đường thẳng \(AC,BD,MP,NQ\) trong đó \(M,N,P,Q\) lần lượt là trung điểm các cạnh \(AB,BC,CD,AD\)(hình 3.81). Vì sao bốn đường cắt này đồng quy?
Tính độ dài đường chéo hình vuông có:
a) Chu vi bằng 12
b) Diện tích bằng 25
Cho hình vuông ABCD có cạnh dài \(4\,cm\) và \(M,N,P,Q\) lần lượt là trung điểm các cạnh \(AB,BC,CD,AD.\)
a) Chứng minh rằng tứ giác MNPQ là hình vuông.
b) Tính diện tích hình vuông MNPQ.
Cho hình vuông ABCD. Lấy E, F, G, H theo thứ tự thuộc các cạnh AB, BC, CD, DA sao cho \(AE = BF = CG = DH = a\); \(BE = CF = DG = AH = b\). Chứng minh rằng:
a) Tứ giác EFGH là hình gì?
b) Tính diện tích tứ giác EFGH theo a và b.
Điền cụm từ thích hợp vào chỗ trống
a) Nếu ABCD là một hình vuông thì ta có: AC = ......, AC vuông góc với ......., AC cắt BD tại ............................. mỗi đường, AC là ................................ của góc A, BD là ........................ của góc D.
b) ............................................................. có hai đường chéo vuông góc là hình vuông.
c) Hình chữ nhật có một đường chéo là ....................................................... hình vuông.
d) Hình chữ nhật có ......................................... là hình vuông.
e) Hình thoi ................................ là hình vuông.
f) Hình thoi có ..................................... bằng nhau là hình vuông.
n – giác gọi là n – giác đều nếu tất cả các cạnh của nó bằng nhau và tất cả các góc của nó bằng nhau.
a) Tính số đo mỗi góc của một n – giác đều.
b) Tứ giác đều là hình gì?
