Cho tứ giác EKIT có \(EK = ET,IK = IT,\widehat {KET} = {90^0},\widehat {EKI} = {105^0}\). Gọi S là giao điểm của hai đường chéo. Tính số đo các góc \(\widehat {KIS},\widehat {SKI}\)
Sử dụng kiến thức về đường chéo của tứ giác để tìm số đo góc còn lại: Trong tứ giác, đường chéo là đoạn thẳng nối hai đỉnh đối nhau
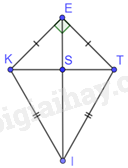
Vì \(EK = ET\) nên E thuộc đường trung trực của KT.
Vì \(IK = IT\) nên I thuộc đường trung trực của KT.
Do đó, EI là đường trung trực của KT. Suy ra: \(EI \bot KT\) tại S.
Tam giác EKT có: \(EK = ET\), \(\widehat {KET} = {90^0}\) nên tam giác EKT vuông cân tại E. Do đó, ES là đường trung trực đồng thời là đường phân giác. Do đó, \(\widehat {KES} = \frac{1}{2}\widehat {KET} = {45^0}\)
Tam giác KEI có: \(\widehat {KIE} = {180^0} - \widehat {EKI} - \widehat {KES} = {30^0}\)
Tam giác KIS vuông tại S có: \(\widehat {SKI} = {90^0} - \widehat {KIS} = {90^0} - {30^0} = {60^0}\)
Các bài tập cùng chuyên đề
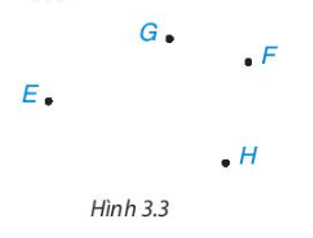
Cho bốn điểm E, F, G, H (Hình 3.3). Kể tên một tứ giác có các đỉnh là bốn điểm đã cho.
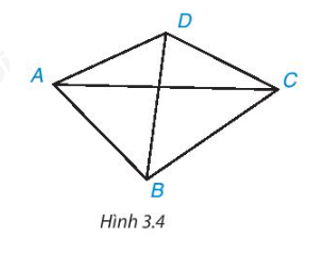
Quan sát tứ giác ABCD trong Hình 3.4.
Hai đỉnh không cùng thuộc một cạnh gọi là hai đỉnh đối nhau. Đoạn thẳng nối hai đỉnh đối nhau là một đường chéo, chẳng hạn AC là một đường chéo. Kể tên đường chéo còn lại.
- Cặp cạnh AB, CD là cặp cạnh đối. Chỉ ra cặp cạnh đối còn lại.
- Cặp góc A, C là cặp góc đối. Hãy kể tên cặp góc đối còn lại.
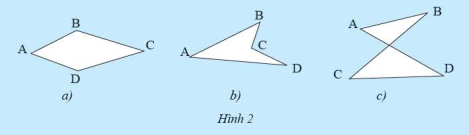
Vẽ các đường thẳng lần lượt chứa mỗi cạnh của các tứ giác sau đây và nêu nhận xét của em về vị trí của mỗi tứ giác đối với mỗi đường thẳng đã vẽ.
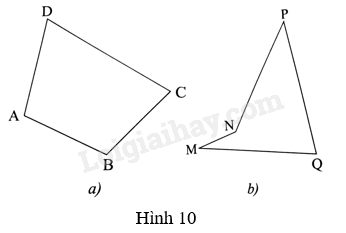
Vẽ tứ giác \(MNPQ\) và tìm:
- Hai đỉnh đối nhau
- Hai đường chéo
- Hai cạnh đối nhau
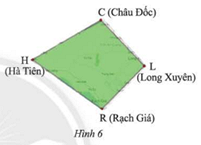
Tìm các đỉnh, cạnh và đường chéo của tứ giác Long Xuyên \(CHRL\) (Hình 6)
Trên bản đồ, tứ giác \(BDNQ\) với các đỉnh là các thành phố Buôn Ma Thuột, Đà Lạt, Nha Trang, Quy Nhơn.
a) Tìm các cạnh kề và cạnh đối diện của cạnh \(BD\).
b) Tìm các đường chéo của tứ giác
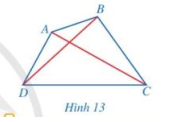
Quan sát tứ giác ABC ở hình 13 và đọc tên các cạnh, các đường chéo, các đỉnh, các góc của tứ giác đó.
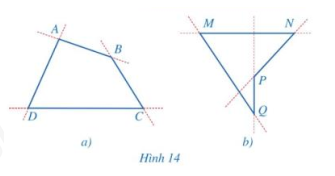
Quan sát các hình 14a, 14b và nêu nhận xét về vị trí của mỗi tứ giác so với đường thẳng chứa một cạnh bất kì của tứ giác đó.
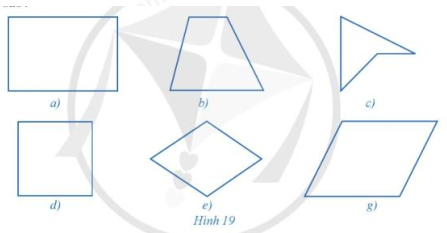
Trong các tứ giác ở hình 19a, 19b, 19c, 19g, tứ giác nào không phải là tứ giác lồi? Vì sao?
Trong trường hợp nào ở Hình 3.16, tứ giác \(ABCD\) nằm về cùng một phía của từng đường thẳng trong các đường thẳng \(AB,BC,CD\) và \(DA\).
Vẽ ba điểm A, B, C không thẳng hàng bất kì. Hãy vẽ thêm điểm D và E sao cho tứ giác ABCD lồi còn tứ giác ABCE không lồi.
Viết tên tất cả các cặp cạnh kề nhau, cặp cạnh đối nhau, cặp đỉnh kề nhau, cặp đỉnh đối nhau còn lại của tứ giác \(ABCD\) trong Hình 3.17.
Chứng minh tổng độ dài hai đường chéo của tứ giác:
a) Bé hơn chu vi của tứ giác;
b) Lớn hơn tổng hai cạnh đối tùy ý của tứ giác, từ đó lớn hơn nửa chu vi của tứ giác.
Tìm điểm M bên trong tứ giác ABCD sao cho tổng khoảng cách từ M đến bốn đỉnh A, B, C, D là bé nhất.
Tìm tứ giác lồi trong các hình sau:
Chứng minh rằng trong một tứ giác, tổng độ dài hai đường chéo lớn hơn nửa chu vi tứ giác đó.
Chứng minh rằng: Trong một tứ giác, tổng độ dài hai đường chéo lớn hơn tổng độ dài hai cạnh đối.
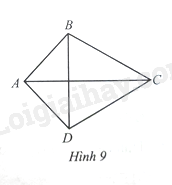
Thả diều là một trò chơi dân gian của nhiều trẻ em ở Việt Nam cũng như ở nhiều nước trên thế giới. Một tứ giác \(ABCD\) với \(AB = AD,BC = CD\) gọi là hình “chiếc diều” (Hình 9)
a) So sánh \(\widehat B\) và \(\widehat D\).
b) Tìm mối liên hệ giữa hai đường chéo \(AC\) và \(BD\)
